转载:http://www.cnblogs.com/jingmoxukong/p/4303279.html
要点
希尔(Shell)排序又称为缩小增量排序,它是一种插入排序。它是直接插入排序算法的一种威力加强版。该方法因DL.Shell于1959年提出而得名。
希尔排序的基本思想是:
把记录按步长 gap 分组,对每组记录采用直接插入排序方法进行排序。 随着步长逐渐减小,所分成的组包含的记录越来越多,当步长的值减小到 1 时,整个数据合成为一组,构成一组有序记录,则完成排序。
我们来通过演示图,更深入的理解一下这个过程。
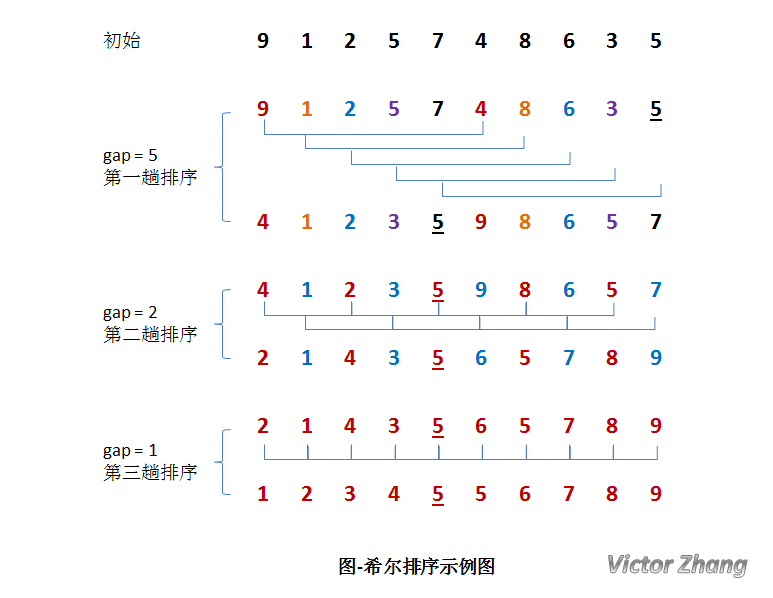
在上面这幅图中:
初始时,有一个大小为 10 的无序序列。
在第一趟排序中,我们不妨设 gap1 = N / 2 = 5,即相隔距离为 5 的元素组成一组,可以分为 5 组。
接下来,按照直接插入排序的方法对每个组进行排序。
在第二趟排序中,我们把上次的 gap 缩小一半,即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组,可以分为 2 组。
按照直接插入排序的方法对每个组进行排序。
在第三趟排序中,再次把 gap 缩小一半,即gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成一组,即只有一组。
按照直接插入排序的方法对每个组进行排序。此时,排序已经结束。
需要注意一下的是,图中有两个相等数值的元素 5 和 5 。我们可以清楚的看到,在排序过程中,两个元素位置交换了。
所以,希尔排序是不稳定的算法。
核心代码
void shellSort(int *a,int n){ int gap=n/2; while(gap>=1){ //把距离为gap的元素编为一个组,扫描所有组 for(int i=gap;i<n;i++){ int j=0; int temp=a[i]; //对距离为gap的元素组进行排序 for(j=i-gap;j>=0&&temp<a[j];j=j-gap)//一定要注意!!! a[j+gap]=a[j]; a[j+gap]=temp; } gap/=2;//减少增量 } }
算法分析
希尔排序的算法性能
|
排序类别 |
排序方法 |
时间复杂度 |
空间复杂度 |
稳定性 |
复杂性 |
||
|
平均情况 |
最坏情况 |
最好情况 |
|||||
|
插入排序 |
希尔排序 |
O(Nlog2N) |
O(N1.5) |
|
O(1) |
不稳定 |
较复杂 |
时间复杂度
步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。
算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序,最终算法以步长为1进行排序。当步长为1时,算法变为插入排序,这就保证了数据一定会被排序。 Donald Shell 最初建议步长选择为N/2并且对步长取半直到步长达到1。虽然这样取可以比O(N2)类的算法(插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。可能希尔排序最重要的地方在于当用较小步长排序后,以前用的较大步长仍然是有序的。比如,如果一个数列以步长5进行了排序然后再以步长3进行排序,那么该数列不仅是以步长3有序,而且是以步长5有序。如果不是这样,那么算法在迭代过程中会打乱以前的顺序,那就不会以如此短的时间完成排序了。
已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,...)
这项研究也表明“比较在希尔排序中是最主要的操作,而不是交换。”用这样步长序列的希尔排序比插入排序和堆排序都要快,甚至在小数组中比快速排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。
算法稳定性
由上文的希尔排序算法演示图即可知,希尔排序中相等数据可能会交换位置,所以希尔排序是不稳定的算法。
直接插入排序和希尔排序的比较
直接插入排序是稳定的;而希尔排序是不稳定的。
直接插入排序更适合于原始记录基本有序的集合。
希尔排序的比较次数和移动次数都要比直接插入排序少,当N越大时,效果越明显。
在希尔排序中,增量序列gap的取法必须满足:最后一个步长必须是 1 。
直接插入排序也适用于链式存储结构;希尔排序不适用于链式结构。
运行结果