https://chortle.ccsu.edu/VectorLessons/index.html
Chapter0 Points and Lines (已看)
Chapter1 Vectors, Points, and Column Matrices (已看)
Chapter5 Vector Direction (已看)
Chapter6 Scaling and Unit Vectors (已看)
Chapter8 Length and The Dot Product (已看)
Chapter9 The Angle between Two Vectors (已看)
Chapter10 The Angle between 3D Vectors (已看)
Chapter11 Projecting one Vector onto Another (已看)
Chapter12 Vector Cross Product (已看)
Chapter13 Matrices and Simple Matrix Operations (已看)
Chapter14 Matrix-Column Matrix Multiplication (已看)
Chapter15 Matrix-Matrix Multiplication (已看)
Chapter16 Identity Matrix and Matrix Inverse (已看)
Chapter0 Points and Lines
Q1: What is a point?
A: A point is a location in space.
Q2: If you had the spike lying in front of you on your desk, would you consider its end to be a point?
A: Probably not.On that scale, the end is too blunt to be considered a point.
Points in 3D space are an idealization.
The column matrix and the point are different things.One is used to represent the other, just as your name is used to represent you.
Q17: A point has only one property:location. A vector has two properties:length and direction but does not have location
Chapter1 Vectors, Points, and Column Matrices
Q1: What two types of geometrical objects are represented with column matrices?
(1)Points,and (2) Vectors
Column matrices are awkward in printed text.It is common to print a column matrix like this: (2.9,-4.6,0.0)T.The "T" stands for transpose, which means to change rows into columns.
Only matrices of the same type can be compared.It makes no sense to compare a three-dimensional row matrix to a three-dimensional column matrix.
Chapter2 Matrix Addition
Chapter3 Vector Addition
The vital (and often confusing) idea is that in a graphics program there is one virtual world, but any number of coordinate frame might be in use.Often, each object has its own frame, a different frame is used to describe locations of objects, and another frame might be used for the viewpoint.
Q10: Both points and vectors are represented with column matrices. Is this likely to be confusing?
A: Yes. This confusion leads to the use of homogeneous coordinates, another way to represent points and vectors with coumn matrices.
Sometimes the operation of adding a vector to a point is called translation.The original point is sometimes said to have been "translated to a new location"
Chapter4 Vector Length
Chapter5 Vector Direction
The orientation of a vector is usually expressed as an angle with positive x axis of a coordinate frame. There are two ways of doing this:
The angle is 0 to 360 measured as a counter-clockwise rotation from the positive x axis.
The angle is 0 to +180 measured as a counter-clockwise rotation from the positive x axis, or is 0 to -180 measured as clockwise rotation from the positive x axis
The formula for the direction of a 2D vector is
angle of (x, y)T = arc tan(y / x)
Arc tan(z) means "find the angle that has a tangent of z"
In most programming languages, the function atant2(y, x) is available. It computes the angle in radians between the positive x-axis and the point given by the coordinates(x, y). It uses the signs of x and y to determine the correct quardrant for the angle.
Chapter6 Scaling and Unit Vectors
A unit vector is a vector with a length of one
Chapter7 The Dot Product
Chapter8 Length and The Dot Product
A vector that is perpendicular to a particular surface is sometimes called a "normal vector" but is not necessarily a unit vector.
Recall the formula: angle = arc tan(y / x)
This forumla si not very useful in three dimensions. When there are three axes it is not enough to determine the angle between a vector and just one axis
Often the unit vector for a given vector is used to express the given vector's direction.There is only one such unit vector. so this description of direction is unique. This works for all dimensions.
A unit normal to a given vector is a vector that
1. Is orthogonal(normal) to the given vector.
2. Has a length of one.
Chapter9 The Angle between Two Vectors
Chapter10 The Angle between 3D Vectors

Any two of the three edges of a corner of a cardboard box lie in a plane. The angle between them is 90
All the edges of the box intersect at right angles. When the edges are projected to form a 2D picture the angles between the edges are usually not 90
Q2: If your viewpoint changes, do the angles between the edges of the box change?
A: No. Changing your viewpoint does not change the 3D objects. But the 2D picture changes.
The angle between two vectors in 3D depends on their relation to each other (and does not depend on your viewpoint, or the coordinates frame you are using).Of course, when a 2D picture shows a 3D scene the angles in the picture very much depend on the viewpoint.
Q7: Do two vectors need to be touching at their tails for there to be an angle between them?
A: No. Vectors don't really have a position. You can take the dot product of any two 3D vectors or the column matrices that represent them.
Chapter11 Projecting one Vector onto Another
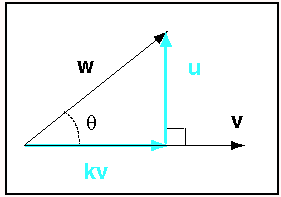
In the diagram w and v are any two vectors. We want a vector u that is orthogonal to v. And we want scalar k so that
w = kv + u
Then kv is called the projection of w onto v.
Unit vectors are used to represent orientation in 3D space.
The length of kv = |w|cosθ
The orientation of kv is vu
kv = |w|(wu·vu)vu
Chapter12 Vector Cross Product
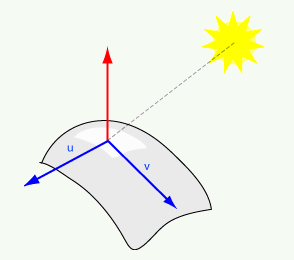
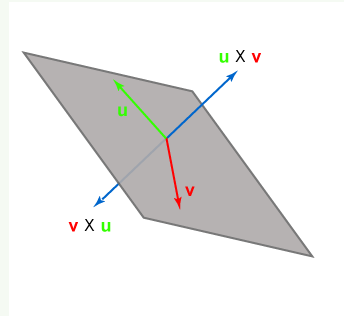
The cross product is another operation that takes two vectors as operands. The most important use of the cross product in computer graphics is to find a vector perpendicular to a plane. This is needed when calculating how light reflects off the surface.
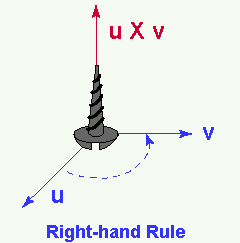
Definition of the Cross product u x v
u and v must be 3D vectors
The result is a 3D vector with the following length and orientation:
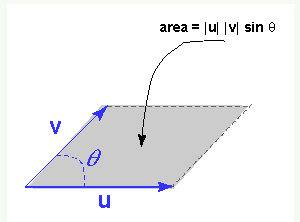
Length:|u x v| = |u||v|sinθ,where θ, is the angle between u and v
Orientation: u x v is perpendicular to both u and v
The choice (out of two) orientations perpendicular to u and v is made by the right hand rule

Definition of the cross product for column matrices u x v
u and v must represent 3D vectors
The result represents a 3D vector
If vector u is represented by u = (ui,uj,uk)T
and if vector v is represented by v = (vi,vj,vk)T
Then u x v = (ujvk - ukuj, ukvi - uivk, uivj - ujui)
Chapter13 Matrices and Simple Matrix Operations
The numbers of rows and columns of a matrix are called it's dimensions.
A square matrix has the same number of rows and columns.
A rectangular matrix is one where the number of rows or columns may not be the same.
A column matrix consists of a single column.
A row matrix consists of a single row.
Some books call a column matrix a column vector and call a row matrix a row vector. This is OK, but can be ambiguous. In these notes the word vector will be used for a geometric object.
In these nteos, column matrices will be used to represent vectors and will also be used to represent geometric points.
Q4: What are square matrices used for?
A: Square matrices are used (in computer graphics) to represent geometric transformations.
A symmetric matrix is equal to it's transpose: AT = A
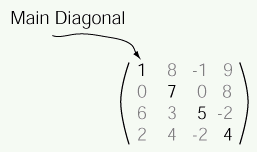
The main diagonal of a matrix consists of those elements that lie on the diagonal that runs from top left to bottom right.
If the matrix is A, then it's main diagnoal are the elements who's row number and column number are equal
The other diagonal of a matrix is not important and does not have a name.
Chapter14 Matrix-Column Matrix Multiplication
Chapter15 Matrix-Matrix Multiplication
Chapter16 Identity Matrix and Matrix Inverse
The matrix I is called an identity matrix because IA = A and AI = A for all matrices A.
This is similar to the real number 1, which is called the multiplicative identity, because 1a = a and a1 = a for all real numbers a.
There is no matrix that works as an identity for matrices of all dimensions. For N x N sqaure matrices there is a matrix INxN that works as an identity.
The N-dimensional identity matrix INxN has 1 on the main diagnoal and 0 elsewhere
A matrix that does have an inverse is called non-singular. A matrix tha does not is called singular. If the matrix A is non-sigular, then
AA-1 = A-1A = I
A non-singular matrix has a corresponding inverse. A singular matrix is all alone.it has no inverse
The inverse of a non-singular square matrix is unique.
The determinant of a singular matrix is zero
The rank of a matrix is the maximum number of independent rows (or, the maximum number of independent columns). A square matrix Anxn is non-singular only if it's rank is equal to n.