单调栈的应用 --- 笛卡尔树与虚树

笛卡尔树

何为笛卡尔树？

对于一组关系(fa, ls, rs)

满足(pri[fa] geqslant max(pri[ls], pri[rs]))

以及(val[rs] geqslant val[fa] geqslant val[ls])

如何构建笛卡尔树？

按照(val)顺序顺序插入(n)个点

那么，新插入的点一定会插入到最右边(最大)

那么，我们维护最右链

同时，注意到最右链中(pri)单调

因此可以维护一个单调栈，来即时地找到插入位置

void Tree() {
    for(int i = 1; i <= n; i ++) {
        pri[i] = rand();
        while(top && pri[s[top]] > pri[i])
        ls[i] = s[top], top --;
        fa[i] = s[top]; fa[ls[i]] = i; 
        if(fa[i]) rs[fa[i]] = i;
        s[++ top] = i;
    }
}

建树的方法2

每次选取区间最大值作为根，然后往两边递归也可以建树

直接暴力是(O(n^2))的

线段树优化一下就可以(O(n log n))了

---

一些常见的题目：

[HNOI2016]序列

[IOI2018]meeting

luoguP4755

CF1117G

[ZJOI2012]小蓝的好友

虚树

在一棵树中，把给定点及相关的(lca)求出来后按照原树的构造连接成的树

定理一：
树中(k)个节点之间两两之间不同的(lca)至多有(k - 1)个
证明：使用欧拉序

考虑(dfs)序最大的一条链

按照(dfs)序排序后，我们尝试依次加入点(a)

那么，点(a)要么新开一条链，要么对(dfs)序最大的链产生影响

只要用一个单调栈来维护当前链即可

同时，为了方便，约定退栈连边

具体而言，有以下几种情况

我们假设(v)是栈顶元素，(w)是栈中排第二的元素

(root)是(k)个点中(dfs)序最小的点（即虚树根），(lca)是(v)和(a)的最近公共祖先

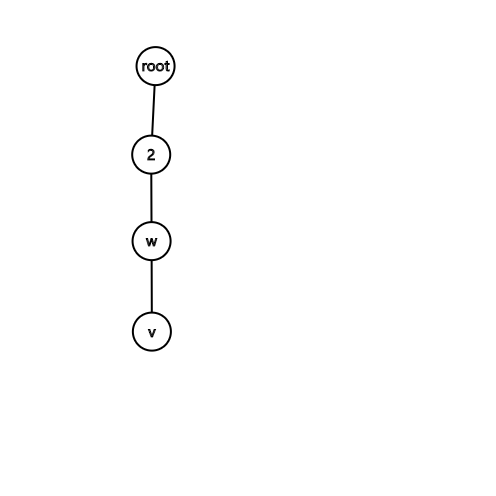
假设原链的形式类似于此

第一种情况：

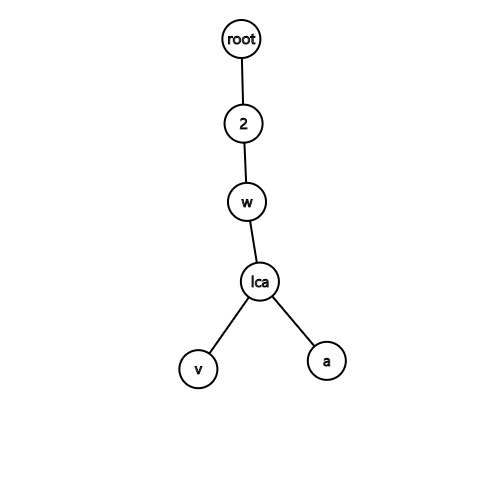
这种情况下，(v)退栈，((v, lca))需要被连接，(lca, a)依次进栈

第二种情况：

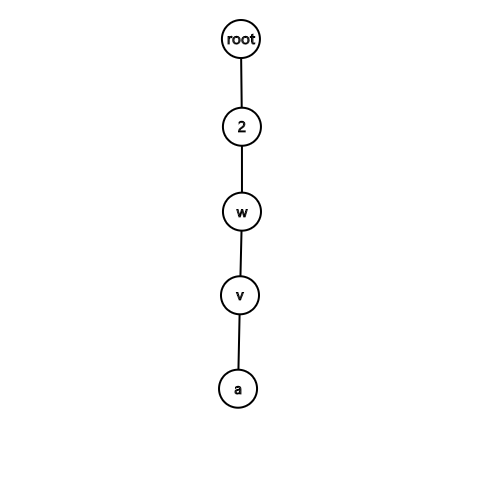
(a)直接进栈即可

第三种情况：

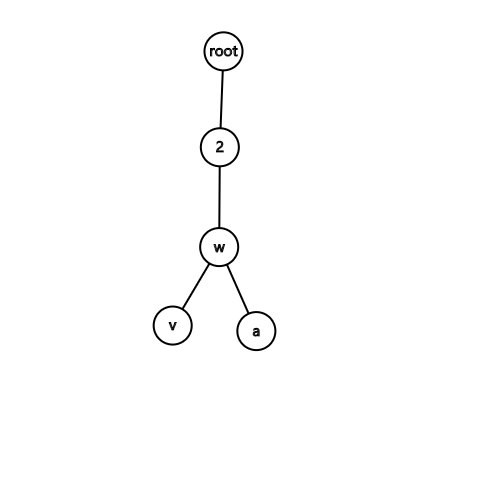
(v)退栈，((v, w))连接，(a)进栈

第四种情况：

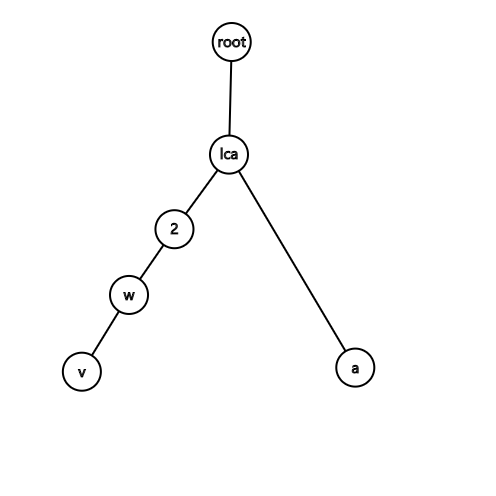
(v)退栈，((v, w))连接之后情况没有什么变化
(w)成为新的(v)，继续操作直到变为情况1, 3

因此，总结一下步骤

1. 先插入虚树根
2. 依次插入后(i)个点
3. 求出(a)与(v)的(lca)
4. 如果(lca = v)，跳到第7步
5. 如果(dfn[w] >= dfn[lca])，(v)退栈，((v, w))连接，重复此步骤
6. 如果(dfn[w] < dfn[lca]), (v)退栈，((v, lca))连接，(lca)入栈
   否则(v)退栈，((v, w))连接
7. (a)入栈
8. 重复第(2)至第(7)步
9. 最后处理栈中剩下的最后一条链

给个本人的实现吧....

inline bool cmp(int a, int b) { return dfn[a] < dfn[b]; }

//dfn数组为dfs序，dep数组为节点深度
//h数组存储所有的关键点，总共有K个
//st为栈
void Vitural_Tree {
    sort(h + 1, h + K + 1, cmp);
    st[top = 1] = 1;
    for(ri i = 1; i <= K; i ++) {
        int rem = lca(st[top], h[i]);
        if(rem == st[top]) { st[++ top] = h[i]; continue; }
        while(top > 1 && dep[st[top - 1]] >= dep[rem])
        { link(st[top - 1], st[top]); top --; }
        if(dep[st[top]] > dep[rem]) link(rem, st[top]), top --;
        if(rem != st[top]) st[++ top] = rem; 
        if(h[i] != st[top]) st[++ top] = h[i];
    }
    while(top > 1) link(st[top - 1], st[top]), top --;
}

虚树题目的显著特征：(sum k leq 3 * 10^5)（当然有的时候并不是）

[SDOI2011]消耗战

[HEOI2014]大工程

[HNOI2014]世界树

PKUWC2019 你和虚树的故事（不知道什么时候公开呢....）

---

有关虚树的扩展

虚树套数据结构：

luoguP4242 树上的毒瘤

动态维护虚树信息：

[SDOI2015]寻宝游戏

真.动态虚树：（也可能是个假的

bzoj5402 f

---