给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/
2 2
/ /
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/
2 2
3 3
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/symmetric-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
1.递归
如果一个树的左子树与右子树镜像对称,那么这个树是对称的
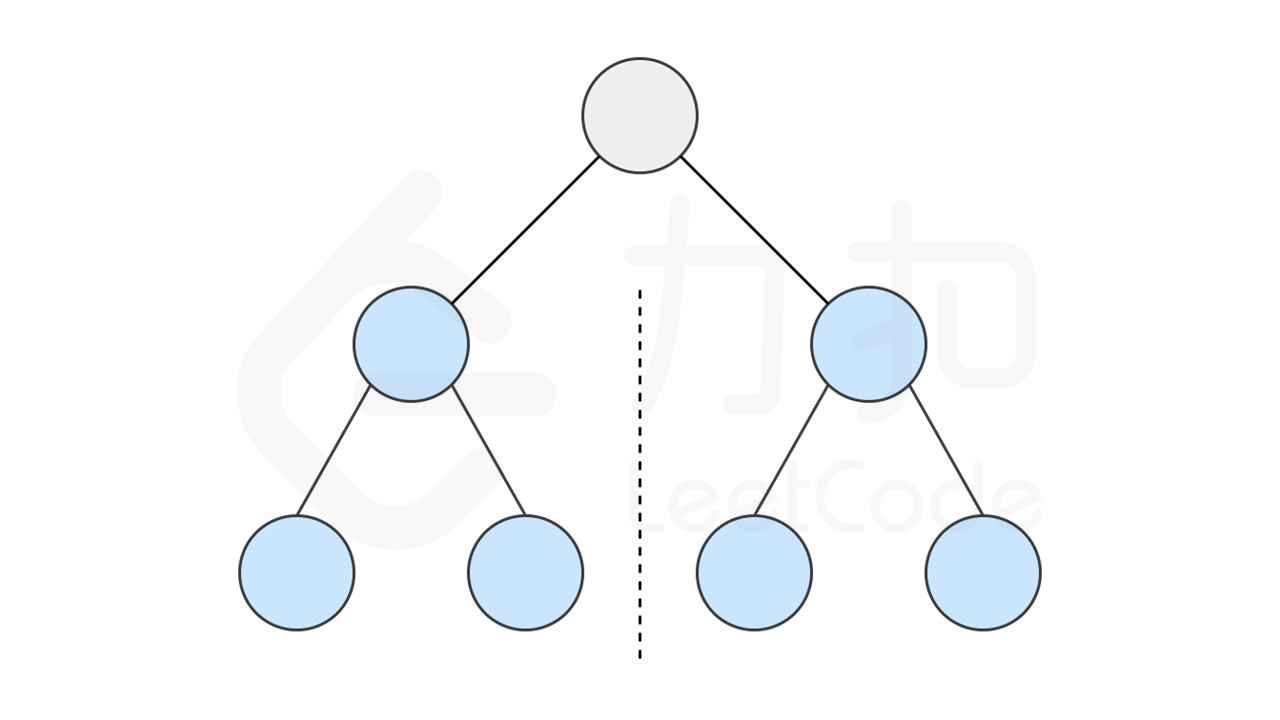
因此,该问题转化为,判断两个左右子树是否彼此镜像
也即判断是否满足以下镜像条件:
1.两子树的根节点值相等
2.一子树的右子树与另一子树的左子树镜像对称,一子树的左子树与另一子树的右子树镜像对称
也就产生了递归关系。
代码表述如下:
class Solution { private: bool isMirror(TreeNode* t1,TreeNode* t2) { if(t1==NULL && t2==NULL) return true; if(!t1 || !t2) return false;return isMirror(t1->left,t2->right) && isMirror(t1->right,t2->left); } public: bool isSymmetric(TreeNode* root) { if(root==NULL) return true; return isMirror(root,root); } };
迭代法:
思路与上面所述相同,但是采用两个队列实现,队列q1存储左树上的节点,q2存储右树上的节点
class Solution { public: bool isSymmetric(TreeNode* root) { if(root==NULL) return true; queue<TreeNode*>q1; queue<TreeNode*>q2; q1.push(root); q2.push(root); TreeNode* curr1,*curr2; while(q1.size() && q2.size()) { curr1 = q1.front(); q1.pop(); curr2 =q2.front(); q2.pop(); if(curr1==NULL && curr2==NULL) continue; if(!curr1 || !curr2) return false; if(curr1->val == curr2->val) { q1.push(curr1->left); q1.push(curr1->right); q2.push(curr2->right); q2.push(curr2->left); } else return false; } return true; } };