Leetcode162. 寻找峰值

峰值元素是指其值大于左右相邻值的元素。

给定一个输入数组 nums，其中 nums[i] ≠ nums[i+1]，找到峰值元素并返回其索引。

数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞。

示例 1:

输入: nums = [1,2,3,1]
输出: 2
解释: 3 是峰值元素，你的函数应该返回其索引 2。
示例 2:

输入: nums = [1,2,1,3,5,6,4]
输出: 1 或 5
解释: 你的函数可以返回索引 1，其峰值元素为 2；
  或者返回索引 5， 其峰值元素为 6。
说明:

你的解法应该是 O(logN) 时间复杂度的。

二分查找

算法

我们可以将 numsnums 数组中的任何给定序列视为交替的升序和降序序列。通过利用这一点，以及“可以返回任何一个峰作为结果”的要求，我们可以利用二分查找来找到所需的峰值元素。

在简单的二分查找中，我们处理的是一个有序数列，并通过在每一步减少搜索空间来找到所需要的数字。在本例中，我们对二分查找进行一点修改。首先从数组 numsnums 中找到中间的元素 midmid。若该元素恰好位于降序序列或者一个局部下降坡度中（通过将 nums[i]nums[i] 与右侧比较判断)，则说明峰值会在本元素的左边。于是，我们将搜索空间缩小为 midmid 的左边(包括其本身)，并在左侧子数组上重复上述过程。

若该元素恰好位于升序序列或者一个局部上升坡度中（通过将 nums[i]nums[i] 与右侧比较判断)，则说明峰值会在本元素的右边。于是，我们将搜索空间缩小为 midmid 的右边，并在右侧子数组上重复上述过程。

就这样，我们不断地缩小搜索空间，直到搜索空间中只有一个元素，该元素即为峰值元素。

为了理解本方法的原理，让我们再次讨论前文提到的全部三种情况。

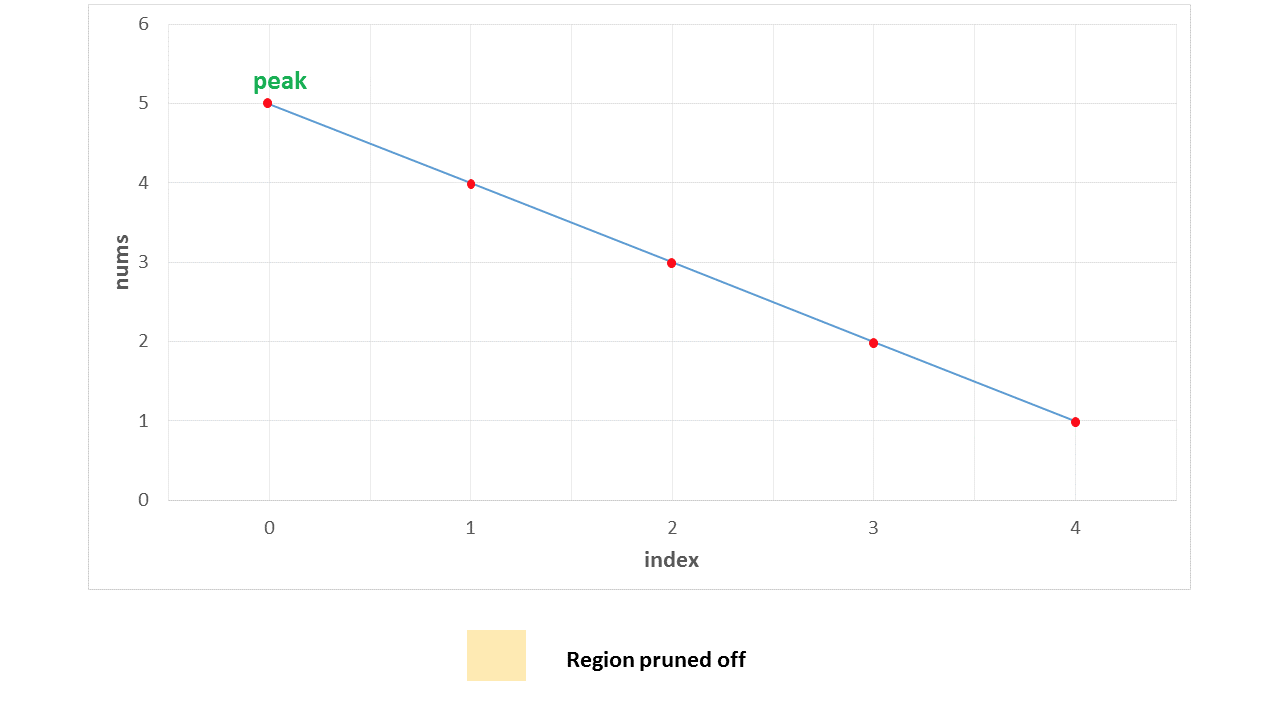
情况 1. 这种情况下，首先找到中间元素 33。由于它处于下降坡度，将搜索空间缩小到 [1, 2, 3]。对于此子数组，22 为中间元素，也处于下降坡度中，于是将搜索空间缩小到 [1, 2]。现在 11 是中间元素并同样处于下降坡度，于是将搜索空间缩小到 [1]。 最终 11 作为答案被正确返回。

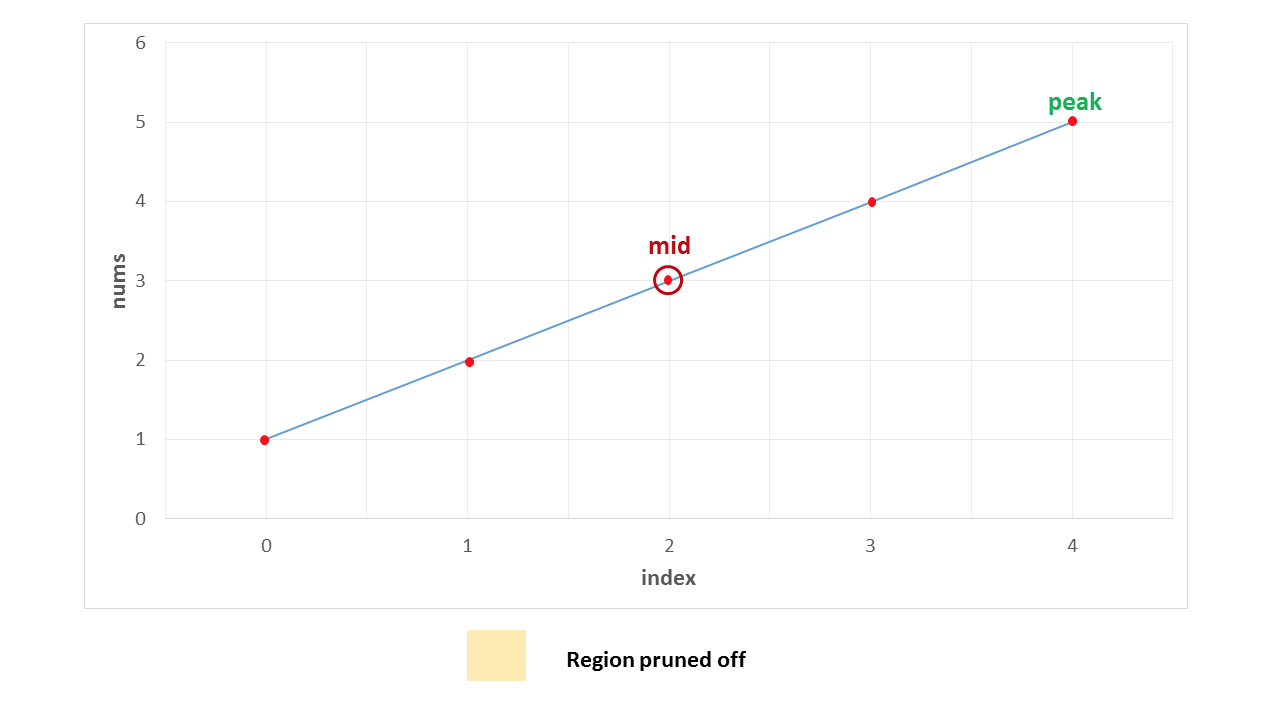
情况 2. 这种情况下，首先找到中间元素 33。由于它处于上升坡度，将搜索空间缩小到 [4, 5]。对于此子数组，44 为中间元素，也处于上升坡度中，于是将搜索空间缩小到 [5]。 最终 55 作为答案被正确返回。

。

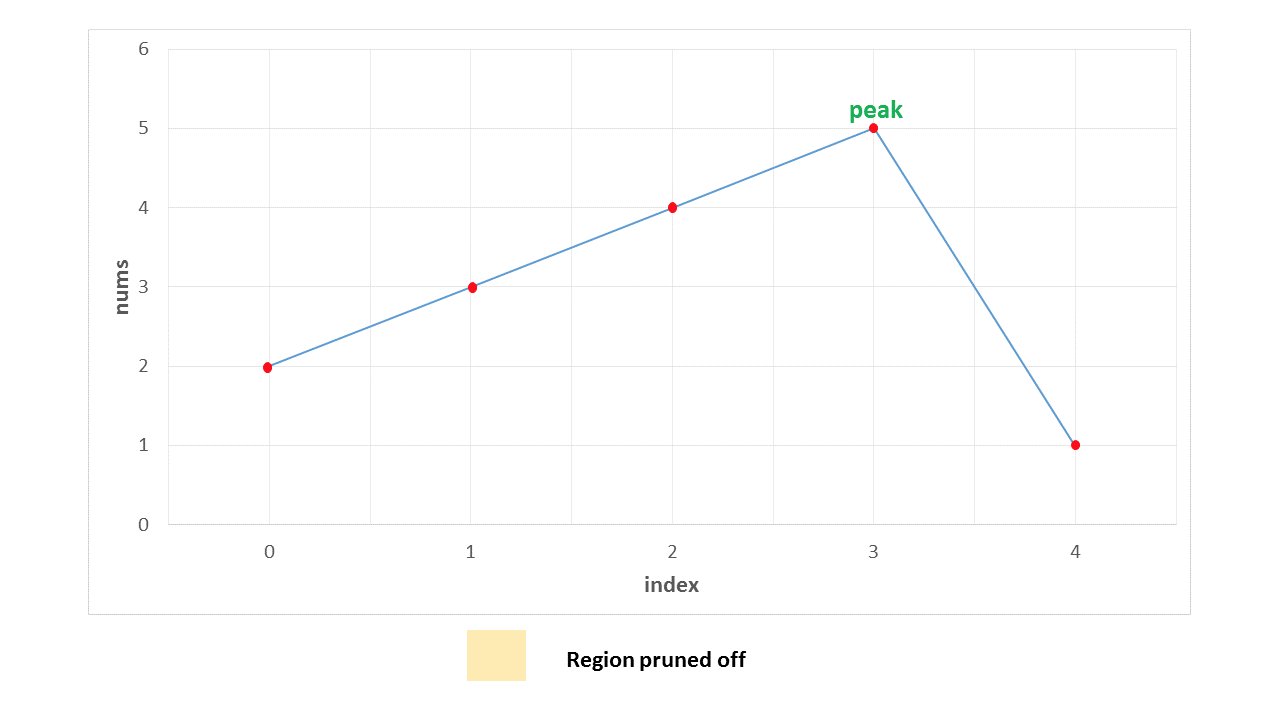
情况 3. 这种情况下， 峰值位于中间某处。第一个中间元素是 44。它位于上升坡度，表明峰值在其右侧。于是，搜索空间缩小为 [5, 1]。 现在，55 位于下降坡度（相对其右侧相邻元素）, 搜索空间下降为 [5]。于是，55 被正确识别。

 

 迭代二分法

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int left=0;
        int right=nums.size()-1;
        int middle=0;
        while(left<right)
        {
            middle=left+(right-left)/2;
            if(nums[middle]>nums[middle+1])
                right=middle;
            else if(nums[middle]<nums[middle+1])
                left=middle+1;
        }
        return left;
        
    }
};

递归二分法：

class Solution{
private:
    int search(vector<int>& nums,int left,int right)
    {
        int middle=left+(right-left)/2;
        if(left==right)
            return left;
        if(nums[middle]>nums[middle+1])
            return search(nums,left,middle);
        return search(nums,middle+1,right);
    }

public:
    int findPeakElement(vector<int>& nums)
    {
        if(nums.size()==0) return -INT_MAX;
        return search(nums,0,nums.size()-1);
    }
};