1.将DFA最小化:教材P65 第9题
解:
|
I |
{1,2,3,4,5} |
{6,7} |
|
{1,2}b->{2} {3,4}b->{6,7} {5}b->ε |
{6,7} |
|
|
II |
{1,2} {3,4}{5} |
{6,7} |
|
{3}c->{3},{4}c->{3} {3}d->{5},{4}d->{5} {3}b->{6},{4}b->{7} 故{3,4}不可区别 {1}b->{2},{2}b->{2} {1}a->{3}.{2}a->{4} 故{1,2}不可区别 |
{6,7}不可区别 |
故最小化后转换矩阵为
|
a |
b |
c |
d |
||
|
1 |
{1,2} |
{3,4} |
{1,2} |
||
|
2 |
{3,4} |
{6,7} |
{3,4} |
{5} |
|
|
3 |
{5} |
{3,4} |
|||
|
4 |
{6,7} |
{6,7} |
故DFA最小化为
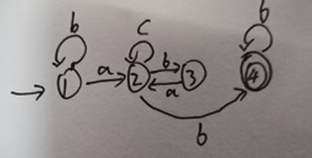
2.构造以下文法相应的最小的DFA
S→ 0A|1B
A→ 1S|1
B→0S|0
解:
S->0(1S|1)|1(0S|0)
S->01S|01|10S|10
S->01S|10S|01|10
S->(01|10)S|(01|10)
S->(01|10)*(01|10)
故NFA为
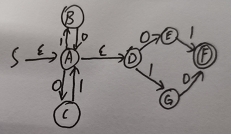
转化为DFA,其转换矩阵为:
|
|
|
0 |
1 |
|
1 |
ε{S}={SAD} |
{CE} |
{BG} |
|
2 |
{CE} |
|
ε{AF}={ADF} |
|
3 |
{BG} |
ε{AF}={ADF} |
|
|
4 |
{ADF} |
{CE} |
{BG} |
通过其转换矩阵得DFA图为
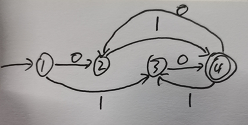
|
I |
{1,2,3} |
{4} |
|
{1}0->{2} {2}0->ε {3}0->{4} |
{4} |
|
|
II |
{1}{2}{3} |
{4} |
发现最开始已经是最下化DFA,故最小化DFA为
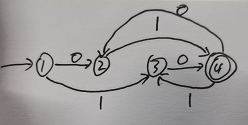
3.给定如下文法 G[S]:
S →AB
A → aA | ɛ
B → b | bB
给出句子aaab 的一个自顶向下语法分析过程,并说明回溯产生的原因是什么?
解:
S -> AB
S -> aAB
S -> aaAB
S -> aaaAB
S -> aaaɛB
S -> aaaɛb
S -> aaab
回溯产生的原因:反复提取公共左因子
4.P100 练习4,反复提取公共左因子,对文法进行改写
解:
A->a( ɛ |C) | bAA
A->aA' | bAA
B->b( ɛ |C) | aBB
B->bB' | aBB
C->bA | aB
C->baA' | aB
C->a(bA' | B)
C->bAA | bB'