前言
- 一场没有AC的考试……
- 考试的时候没有注意时间分配,导致T1T2没有什么时间。
- 又因为一些神奇的原因,暴力又都写挂了。
- 于是我死了。

T1
- 用10分钟打的multiset模拟。
- 结果忘记multiset删元素如果用元素删会把所有该元素都删掉,就Wa0了
- 改成用迭代器删除后T50。
- 后又受milkfun启发打了个对顶multiset。
- 结果还T50,只快了500ms。
- 正解其实很简单,也很暴力。
- 因为每次只会修改很少的元素而取模运算又使s2分布比较均匀,所以中位数的位置变化不大
- 直接开桶记录每个值的出现次数,通过维护小于和大于中位数指针位置数值的数量来进行指针的转移
- 感觉复杂度挺玄学的所以这题是个玄学题

#include<cstdio> #include<set> using namespace std; int const N=179424680,M=1e7+5; int s1[M],s2[M]; int p[M],tot,n,k; bool v[N]; int qj[M],t; int bar[N<<1]; long long ans; inline void getp(){ for(register int i=2;i<N;++i){ if(!v[i])p[++tot]=i; if(tot==n+1)break; for(register int j=1;j<=tot&&i*p[j]<N;++j){ v[i*p[j]]=1; if(!(i%p[j]))break; } } return ; } int main(){ int ww; scanf("%d%d%d",&n,&k,&ww); const int mod=ww; getp(); int lt=k>>1,lit=(k>>1)+1; for(register int i=1;i<=n;++i)s1[i]=1ll*p[i]*i%mod; for(register int i=1;i<=n;++i)s2[i]=s1[i]+s1[i/10+1]; for(register int i=1;i<k;++i)++bar[s2[i]]; if(k&1){ int lf=0,now=-1; for(register int i=k;i<=n;++i){ ++bar[s2[i]]; if(s2[i]<=now)++lf; if(i!=k){ --bar[s2[i-k]]; if(s2[i-k]<=now)--lf; } while(lf<lit)lf+=bar[++now]; while(lf>=lit+bar[now])lf-=bar[now--]; ans+=now; } return printf("%lld.0",ans),0; } int lnow=-1,rnow=-1,lf=0,rf=0; for(register int i=k;i<=n;++i){ ++bar[s2[i]]; if(s2[i]<=lnow)++lf; if(s2[i]<=rnow)++rf; if(i!=k){ --bar[s2[i-k]]; if(s2[i-k]<=lnow)--lf; if(s2[i-k]<=rnow)--rf; } while(lf<lt)lf+=bar[++lnow]; while(lf>=lt+bar[lnow])lf-=bar[lnow--]; while(rf<lit)rf+=bar[++rnow]; while(rf>=lit+bar[rnow])rf-=bar[rnow--]; ans+=lnow+rnow; } printf("%lld.",ans>>1); putchar((ans&1)?53:48); return 0; }
T2
- 用10分钟打的multiset模拟。(模拟总是惊人的相似)
- 结果出题人报复社会分数差不加绝对值,就Wa5了
- 去掉绝对值后T50。
- 正解其实很简单,也很暴力。
- 对于每个p,用一个指针指向前p个最大的数。
- 可以先把第一次操作进行一半,这样每加一个元素就进行一次选择。
- 可以发现指针是不上升的,因为如果新加的一个元素更优就会直接选择,相当于没有添加元素。
- 然后就可以$Theta(N)$扫描了,总的复杂度是$Theta(NK)$。

#include<cstdio> #include<algorithm> using namespace std; int const N=1e5+5,K=2003; inline int read(){ int ss(0);char bb(getchar()); while(bb<48||bb>57)bb=getchar(); while(bb>=48&&bb<=57)ss=(ss<<1)+(ss<<3)+(bb^48),bb=getchar(); return ss; } inline int max(int x,int y){ return x>y?x:y; } int n,k; int a[N],c[N],bar[N]; pair<int,int>b[N]; long long g[2]; int main(){ n=read(),k=read(); for(register int i=1;i<=n;++i)a[i]=read(),b[i]=make_pair(a[i],i); sort(b+1,b+n+1); for(register int i=1,tot=0;i<=n;++i){ if(b[i].first!=b[i-1].first)c[++tot]=b[i].first; a[b[i].second]=tot; } while(k--){ int x=read(),u=1,tp=0; g[0]=g[1]=0; for(register int i=1;i<=x;++i)++bar[a[i]],tp=max(a[i],tp); --bar[tp],g[0]+=c[tp]; while(!bar[tp]&&tp)--tp; for(register int i=x+1;i<=n;++i,u^=1) if(a[i]>=tp)g[u]+=c[a[i]]; else{ ++bar[a[i]],--bar[tp]; g[u]+=c[tp]; while(!bar[tp]&&tp)--tp; } while(tp){ g[u]+=c[tp],--bar[tp],u^=1; while(!bar[tp]&&tp)--tp; } printf("%lld ",g[0]-g[1]); } return 0; }
T3
- 打了两个多小时的树形DP。
- 然后大样例死活过不去心态爆炸。
- 交上去WA44分。
- 考试后发现:
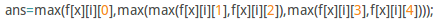
- 改成:
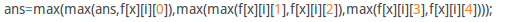
- WA93分。
- 一顿玄学特判AC后觉得自己程序应该不用特判,就又端详了一下代码:

- 把最后一句话删了,AC!
- 不打对拍果然遭天遣了……
- 对于节点i,考虑五种状态:
- f[i][j][0]表示以i的子节点为起点,i为终点,撒了j个面包屑,i和i的直系儿子节点不撒面包屑的最优结果。
- f[i][j][1]表示以i的子节点为起点,i为终点,撒了j个面包屑,i撒面包屑的最优结果。
- f[i][j][2]表示以i的子节点为起点,i为终点,撒了j个面包屑,i不撒面包屑,i的直系儿子撒面包屑的最优方案。
- f[i][j][3]表示以i为起点,i的子节点为终点,撒了j个面包屑,i不撒面包屑的方案数。
- f[i][j][4]表示以i为起点,i的子节点为终点,撒了j个面包屑,i撒面包屑的方案数。
- DP转移与答案统计大约有近20个转移式,max嵌套后有9个,具体看代码吧。
- 复杂度$Theta(5Nv)$。

#include<cstdio> #define ll long long using namespace std; int const N=1e5+1,M=101; int n,v; int head[N],to[N<<1],Next[N<<1],t; int p[N]; ll f[N][M][5],mx[M][5],ans; inline int read(){ int ss(0);char bb(getchar()); while(bb<48||bb>57)bb=getchar(); while(bb>=48&&bb<=57)ss=(ss<<1)+(ss<<3)+(bb^48),bb=getchar(); return ss; } inline void add(int x,int y){ to[++t]=y; Next[t]=head[x],head[x]=t; return ; } inline ll max(ll x,ll y){ return x>y?x:y; } inline ll min(ll x,ll y){ return x<y?x:y; } void dfs(int x,int fa){ ll z(0); for(register int i=head[x];i;i=Next[i]) z+=p[to[i]]; f[x][1][1]=f[x][1][4]=z; for(int i=head[x],y;i;i=Next[i]) if((y=to[i])^fa){ dfs(y,x); mx[1][0]=f[x][1][0],mx[1][1]=f[x][1][1],mx[1][2]=f[x][1][2]; mx[1][3]=f[x][1][3],mx[1][4]=f[x][1][4]; for(register int j=2;j<=v;++j) mx[j][0]=max(mx[j-1][0],f[x][j][0]), mx[j][1]=max(mx[j-1][1],f[x][j][1]), mx[j][2]=max(mx[j-1][2],f[x][j][2]), mx[j][3]=max(mx[j-1][3],f[x][j][3]), mx[j][4]=max(mx[j-1][4],f[x][j][4]); for(register int j=v,jj;j;--j){ f[x][j][0]=max(f[x][j][0],max(f[y][j][0],f[y][j][2])); f[x][j][1]=max(f[x][j][1],max(f[y][j-1][0],max(f[y][j-1][1],f[y][j-1][2]))+z-p[y]); f[x][j][2]=max(f[x][j][2],f[y][j][1]); f[x][j][3]=max(f[x][j][3],max(f[y][j][3],f[y][j][4]-p[x])); f[x][j][4]=max(f[x][j][4],max(f[y][j-1][3],f[y][j-1][4]-p[x])+z); jj=v-j; ans=max(ans,max(mx[jj][0],max(mx[jj][1],mx[jj][2]))+f[y][j][3]); ans=max(ans,max(mx[jj][0],max(mx[jj][1],mx[jj][2]))+f[y][j][4]-p[x]); ans=max(ans,mx[jj][3]+max(f[y][j][0],max(f[y][j][1],f[y][j][2]))); ans=max(ans,mx[jj][4]+max(f[y][j][0],max(f[y][j][1],f[y][j][2]))-p[y]); } } for(register int i=1;i<=v;++i) ans=max(max(ans,f[x][i][0]),max(max(f[x][i][1],f[x][i][2]),max(f[x][i][3],f[x][i][4]))); return ; } int main(){ n=read(),v=read(); for(register int i=1;i<=n;++i)p[i]=read(); for(register int i=1,ff,tt;i<n;++i) ff=read(),tt=read(),add(ff,tt),add(tt,ff); dfs(1,0); printf("%lld",ans); return 0; }
