结对编程——paperOne基于java的四则运算功能改进

　　项目成员：张金生张政

　　由于新的需求，原本使用JSP的实现方式目前改为Java实现，即去除了B/S端。

　　需求分析：

　　1.四则运算要满足整数运算、分数运算两种；

　　2.运算题目随机，并且可以打印题目和答案；

　　3.可以由用户输入答案，并进行对错判断；

　　4.支持括号。

　　5.出现的分数要约分，并且以“m p/n”方式输出。

　　程序概要：

　　1.原本用JSP实现，为满足需求现改用Java实现；

　　2.用户可选择题目数量、题目难度（比如简单难度为两位数加减乘除，中等难度为四位数的加减乘除并包含括号，高难度为四位分数加减乘除等）；

　　3.用户可以选择进入答题还是打印问题与答案；

　　4.答题时输入答案并回车会立即反馈结果；

　　5.整数运算中不仅运算数是整数，结果也一定是整数；

　　6.分数运算结果是约分后的，因此填写的答案也需要约分，否则会判为错。

　　程序运行流程图：

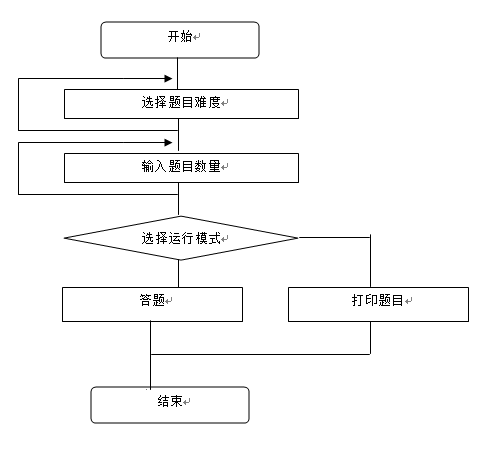
　　实现过程：

　　　　分数类

　　分数类构造函数

　　在构造时直接进行约分操作，其中的maxCommonFactor是分子与分母的最大公约数。

 1        public Fraction(int up, int down) {
 2            if (down == 0 | up == 0) {
 3                System.out.println("divided by zero error");
 4                return;
 5            }
 6            int smaller = up > down ? up : down;
 7            int maxCommonFactor = 1;
 8            for (int i = 1; i <= smaller; i++) {
 9                if (up % i == 0 && down % i == 0) {
10                    maxCommonFactor = i;
11               }
12           }
13   
14           this.up = up / maxCommonFactor;
15           this.down = down / maxCommonFactor;
16       }

　　约分函数

　　与构造函数中的月份操作有所不同，主要用来对进行四则运算后的结果数进行约分操作。

 1      public Fraction gcd(Fraction f) {
 2          int smaller = f.up > f.down ? f.up : f.down;
 3          int maxCommonFactor = 1;
 4          for (int i = 1; i <= smaller; i++) {
 5              if (f.up % i == 0 && f.down % i == 0) {
 6                  maxCommonFactor = i;
 7              }
 8           }
 9          f.up = f.up / maxCommonFactor;
10          f.down = f.down / maxCommonFactor;
11  
12          return f;
13      }

　　转化函数

　　用于最后打印时使分数符合规范。

1      public String toString() {
2          if (down == 1)
3              return "" + up;
4          if(Math.abs(up)/down>0){
5              return up>0?up/down+" "+up%down+"/"+down:"-"+Math.abs(up)/down+" "+Math.abs(up)%down+"/"+down;
6          }
7          return up + "/" + down;
8      }

　　四则运算函数

　　因为数据结构用到了栈，所以减法有些特殊，详情后面会给出解释说明，这里的changesign函数就是用来做减法运算的一个中间函数。

 1       public Fraction add(Fraction f) {
 2           Fraction a = new Fraction(up, down);
 3           a.up = f.up * a.down + a.up * f.down;
 4           a.down = a.down * f.down;
 5   
 6           return a.gcd(a);
 7       }
 8   
 9       public Fraction minus(Fraction f) {
10           Fraction a = new Fraction(up, down);
11           a.up = a.up * f.down - f.up * a.down;
12           a.down = a.down * f.down;
13   
14           return a.gcd(a);
15       }
16   
17       public Fraction multiply(Fraction f) {
18           Fraction a = new Fraction(up, down);
19          a.up = a.up * f.up;
20          a.down = a.down * f.down;
21          return a.gcd(a);
22      }
23  
24      public Fraction divide(Fraction f) {
25          Fraction a = new Fraction(up, down);
26          a.up = a.up * f.down;
27          a.down = a.down * f.up;
28          return a.gcd(a);
29      }
30  
31      public Fraction changeSign(){
32          up = -up;
33          return this;
34      }

　　随机数函数

　　用来随机生成分数。

1       public static Fraction getRandiom(int Max) {
2           return new Fraction((int) (Math.random() * Max / 2) + 1, (int) (Math.random() * Max / 2) + 1);
3       }
4   
5       public static Fraction getRandiom(int Max, boolean isInt) {
6           return new Fraction((int) (Math.random() * Max / 2) + 1, isInt ? 1 : (int) (Math.random() * Max / 2) + 1);
7       }

　　　　题目生成

　　这里包含了括号的随机插入：用ArrayList维护随机生成的括号位置列表，然后使用TreeMap计算并保存应该生成括号的位置，最后在题目生成的时候进行拼接。

  1        public String generateQuestion(int numOfOperand, int rangeMin, int rangMax, SupportedOperation[] operation,
  2                boolean isFractional, boolean hasbracket) {
  3            String question = "";
  4            int[] ioperands = null;
  5            ArrayList<Fraction> af = new ArrayList<Fraction>();
  6            SupportedOperation[] so = null;
  7            if (numOfOperand < 2) {
  8                System.out.println("操作数数量至少为2");
  9                return "";
 10           }
 11           if (rangMax > 500) {
 12               System.out.println("操作数数最大值不能超过500");
 13               return "";
 14           }
 15           getBcPrint(numOfOperand);
 16           if (!isFractional) {
 17               ScriptEngine se = new ScriptEngineManager().getEngineByName("JavaScript");
 18               ioperands = new int[numOfOperand];
 19               for (int i = 0; i < numOfOperand; i++) {
 20                   ioperands[i] = (int) (Math.random() * rangMax / 2 + 1);
 21   
 22               }
 23              so = new SupportedOperation[numOfOperand - 1];
 24               for (int i = 0; i < operation.length; i++) {
 25                   if (operation[i] == SupportedOperation.ALL) {
 26                       operation = new SupportedOperation[4];
 27                       operation[0] = SupportedOperation.ADD;
 28                       operation[1] = SupportedOperation.MINUS;
 29                       operation[2] = SupportedOperation.MULTIPLY;
 30                       operation[3] = SupportedOperation.DIVIDE;
 31   
 32                   }
 33               }
 34               // 除法運算，保证整除
 35               int value = 0;
 36               for (int j = numOfOperand - 1; j > 0; j--) {
 37                   so[numOfOperand - 1 - j] = operation[(int) (Math.random() * operation.length)];
 38               }
 39               for (int j = numOfOperand - 2; j >= 0; j--) {
 40                   if (so[j] == SupportedOperation.DIVIDE) {
 41                       if (value < 1) {
 42                           ioperands[j] = ioperands[j] * ioperands[j + 1];
 43                            value++;
 44   
 45                       } else {
 46                           so[j] = operation[(int) (Math.random() * (operation.length - 2))];
 47                       }
 48                   }
 49               }
 50               // 输出括号
 51               for (int i = 0; i < numOfOperand - 1; i++) {
 52                   if (frequency.containsKey(i)) {
 53                       if (direction.get(i) == 0) {
 54                           for (int k = 0; k < frequency.get(i); k++) {
 55                                question += "(";
 56                           }
 57                       }
 58                   }
 59                   question += ioperands[i];
 60                   if (frequency.containsKey(i)) {
 61                       if (direction.get(i) == 1) {
 62                           for (int k = 0; k < frequency.get(i); k++) {
 63                               question += ")";
 64                           }
 65                       }
 66                   }
 67                   question += so[i];
 68               }
 69               if (frequency.containsKey(numOfOperand - 1)) {
 70                   if (direction.get(numOfOperand - 1) == 0) {
 71                       for (int k = 0; k < frequency.get(numOfOperand - 1); k++) {
 72                           question += "(";
 73                       }
 74                   }
 75               }
 76               question += ioperands[numOfOperand - 1];
 77               if (frequency.containsKey(numOfOperand - 1)) {
 78                   if (direction.get(numOfOperand - 1) == 1) {
 79                       for (int k = 0; k < frequency.get(numOfOperand - 1); k++) {
 80                           question += ")";
 81                       }
 82                   }
 83               }
 84   
 85               try {
 86                   Integer d = (Integer) se.eval(question);
 87                   answer = "" + d;
 88               } catch (Exception e) {
 89                   generateQuestion(numOfOperand, rangeMin, rangMax, operation, isFractional, hasbracket);
 90               }
 91   
 92           } else {
 93               for (int i = 0; i < numOfOperand; i++) {
 94                   af.add(Fraction.getRandiom(rangMax));
 95               }
 96   
 97               so = new SupportedOperation[numOfOperand - 1];
 98               for (int i = 0; i < operation.length; i++) {
 99                   if (operation[i] == SupportedOperation.ALL) {
100                        operation = new SupportedOperation[4];
101                        operation[0] = SupportedOperation.ADD;
102                        operation[1] = SupportedOperation.MINUS;
103                        operation[2] = SupportedOperation.MULTIPLY;
104                        operation[3] = SupportedOperation.DIVIDE;
105    
106                    }
107                }
108                question += af.get(0);
109                for (int j = 0; j < numOfOperand - 1; j++) {
110                    so[j] = operation[(int) (Math.random() * operation.length)];
111                    question += (so[j] == SupportedOperation.DIVIDE ? "÷" : so[j].toString()) + af.get(j + 1);
112   
113                }
114                answer = getanswer(af, so).toString();
115                try {
116                } catch (Exception e) {
117                    e.printStackTrace();
118                }
119            }
120    
121            return question;
122    
123        }
124    }

　　　　括号维护

 1      public String answer;
 2  
 3      Stack<SupportedOperation> oplist = new Stack<SupportedOperation>();
 4      Stack<Fraction> numlist = new Stack<Fraction>();
 5      ArrayList<Integer[]> bclist;
 6      TreeMap<Integer, Integer> frequency;
 7      TreeMap<Integer, Integer> direction;
 8  
 9      private void getBcPrint(int numOfOperand) {
10           bclist = new ArrayList<Integer[]>();
11           if (numOfOperand > 2) {
12               int bcnum = (int) (Math.random() * (numOfOperand - 2));
13               for (int n = 0; n < bcnum; n++) {
14                   Integer[] bracket = new Integer[2];
15                   bracket[0] = (int) (Math.random() * (numOfOperand - 2));
16                   bracket[1] = (int) (Math.random() * (numOfOperand - 2 - bracket[0]) + bracket[0]);
17                   if (bracket[0] == bracket[1]) {
18                       bracket[1]++;
19                   }
20                   boolean canput = true;
21                   for (int i = 0; i < bclist.size(); i++) {
22                       Integer[] tmp = bclist.get(i);
23                       if (bracket[0] < tmp[0] & bracket[1] >= tmp[0] & bracket[1] < tmp[1]) {
24                           canput = false;
25                           break;
26                       } else if (bracket[1] > tmp[1] & bracket[0] > tmp[0] & bracket[0] <= tmp[1]) {
27                           canput = false;
28                           break;
29                       } else if (bracket[0] == tmp[0] & bracket[1] == tmp[1]) {
30   
31                       }
32                    }
33                   if (canput) {
34                       bclist.add(bracket);
35                   }
36               }
37   
38           }
39           frequency = new TreeMap<Integer, Integer>();
40           direction = new TreeMap<Integer, Integer>();
41           for (int i = 0; i < bclist.size(); i++) {
42               Integer[] tmp = bclist.get(i);
43               if (frequency.containsKey(tmp[0])) {
44                   frequency.put(tmp[0], frequency.get(tmp[0]) + 1);
45               } else {
46                  frequency.put(tmp[0], 1);
47                   direction.put(tmp[0], 0);
48               }
49               if (frequency.containsKey(tmp[1])) {
50                   frequency.put(tmp[1], frequency.get(tmp[1]) + 1);
51               } else {
52                   frequency.put(tmp[1], 1);
53                   direction.put(tmp[1], 1);
54               }
55           }
56        }

　　　　计算结果

 1       public Fraction getanswer(ArrayList<Fraction> frlist, SupportedOperation[] so) {
 2   
 3           numlist.push(frlist.get(0));
 4           for (int n = 0; n < so.length; n++) {
 5               switch (so[n]) {
 6               case ADD:
 7                   oplist.push(so[n]);
 8                   numlist.push(frlist.get(n + 1));
 9                   break;
10               case MINUS:
11                   oplist.push(SupportedOperation.ADD);
12                   numlist.push(frlist.get(n + 1).changeSign());
13                   break;
14               case MULTIPLY: {
15                   Fraction r = numlist.pop().multiply(frlist.get(n + 1));
16                   numlist.push(r);
17               }
18                   break;
19               case DIVIDE: {
20                   Fraction r = numlist.pop().divide(frlist.get(n + 1));
21                   numlist.push(r);
22               }
23                   break;
24               default:
25                   System.out.println("不支持的运算");
26                   break;
27               }
28           }
29   
30           while (!oplist.isEmpty()) {
31               Fraction answer = numlist.pop();
32               switch (oplist.pop()) {
33               case ADD: {
34                   answer = answer.add(numlist.pop());
35                   numlist.push(answer);
36               }
37                   break;
38                case MINUS: {
39                   answer = answer.minus(numlist.pop());
40                   numlist.push(answer);
41               }
42                   break;
43                default:
44                    System.out.println("不支持的运算");
45                    break;
46                }
47    
48            }
49    
50            return numlist.pop();
51        }

　　程序运行结果：

　　简单难度答题：

　　普通难度出题打印：

　　复杂题目出题打印：

　　程序退出：

　　结对编程体会

　　两个人在一台电脑上进行编码，其实感觉效率未必会提高，编码速度取决于正在编程的人的打字速度。而且有时候反而会因为在同一问题上看法不同、解决方式不同而产生分歧。不过因为结对编程可以了解到他人的编程思路，也是一种学习的过程。所以本次体会觉得效率提高是其次，互相学习才是最大的收获！

　　争论点：

　　1.整除问题：输出结果在尽量调节为整数的情况下可能因括号的出现导致结果为小数或者分数，对于这样的情况选择直接重出题目（仅限简单和普通难度的问题）；

　　2.分数减法入栈出栈顺序：计算结果采用栈来解决，出栈时仅剩加减法需要运算，当出现减法，甚至连减时选择将减法换为加法运算，然后改变操作数符号，即Fraction.changSign()；

　　3.括号列表维护：括号生成是根据操作数数量决定的，生成括号位置列表时排除无效和冗余括号，最后将括号列表转化位置和括号方向、数量的Map，用于打印括号，即先有操作数后有括号的设计，而不是括号匹配的方式；

　　4.连除问题：用计数器检测除法的出现，防止连除，但是不会妨碍一个题目出现两个或更多的除法运算（仅限简单和普通难度）。因为在整数运算中，为保证可以整除，需要改变被除数，这样做太多次连除会导致最顶层操作数过大，不利于题目平衡性。

　　花费时间较长的问题：括号位置列表生成及维护。

　　工程地址：https://coding.net/u/jx8zjs/p/paperOne/git

SSH: ssh://git@git.coding.net:jx8zjs/paperOne.git

相关阅读:
在Oracle怎样查询表中的top10条记录
 Ant
oracle 时间函数(sysdate)
oracle 时间函数（to_date）
Maven仓库管理器
 数据库中select into from 和 insert into select的区别
 oracle 定时器简单用法
 oraclea 定时器
 XP Home Edition SP2 也可以装 Rational Rose 2003
Unity3D动态天空之UniSky
原文地址：https://www.cnblogs.com/regretless/p/5871378.html

结对编程——paperOne基于java的四则运算 功能改进

结对编程——paperOne基于java的四则运算功能改进