图算法 - 只需“五步” ,获取两节点间的所有路径(非递归方式)
在实现 “图” 数据结构时,会遇到 “获取两点之间是所有路径” 这个算法问题,网上的资料大多都是利用递归算法来实现(见文末的参考文章)。
我们知道在 JS 中用递归算法很容易会让调用栈溢出,为了能在生产环境中使用,必须要用非递归方式的去实现。
经过一番探索,实现的思路主要来自文章 《求两点间所有路径的遍历算法》 ,只是该文中并没有给出具体的实现细节,需要自己去实现;最终本文的实现结合类似《算法 - 调度场算法(Shunting Yard Algorithm)》 中所提及的双栈来完成。
1、算法过程
以计算下图为例, 节点 3 到 节点 6 所有路径所有可能的路径为 8 条:

allpath
我们具体讲一下如何获取这 8 条路径的过程。
首先准备两个栈,分别称为 主栈 和 辅栈:
- 主栈:每个元素是单个节点(Vertex),用于存放当前路径上的节点;
- 辅栈:每个元素用于存放主栈对应元素的 相邻节点列表(Vertex Array);该栈是用来辅助 主栈 的,其长度和 主栈 一致;
Step 1: 建栈
将 v3(节点3)放到主栈,同时将 v3 节点的邻接节点列表 [v1, v7] 放到辅栈中:
首次建栈
主栈和辅栈压入让栈长度增长,我个人称之为 建栈(build stack)

Step 2: 继续建栈
建栈后,我们查看辅栈,其栈顶是节点列表 [v1, v7]:
查看栈顶
我们取出节点列表的第一个元素 v1,将其压入到主栈;同时将剩下的节点列表 [v7] 重新压回到辅栈:
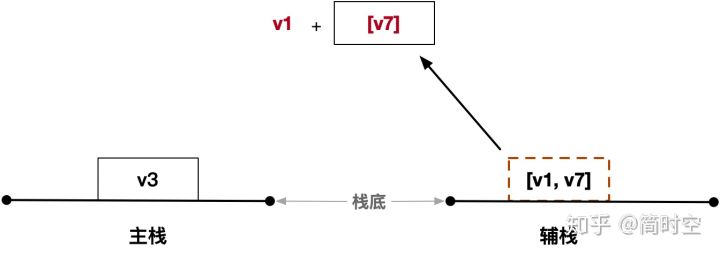
同时查询 v1 的邻接节点列表是 [v3, v0],由于 v3 节点已经在主栈里,需要从这个列表中剔除(这一步很重要),将剔除后的节点列表 [v0] 压入 辅栈 中:

这一步也让主栈和辅栈长度增长了,所以也是 建栈(build stack) 过程
Step 3: 削栈
继续 Step 2 的建栈过程,直到我们的主栈栈顶 v7,此时辅栈的栈顶是空列表 []:
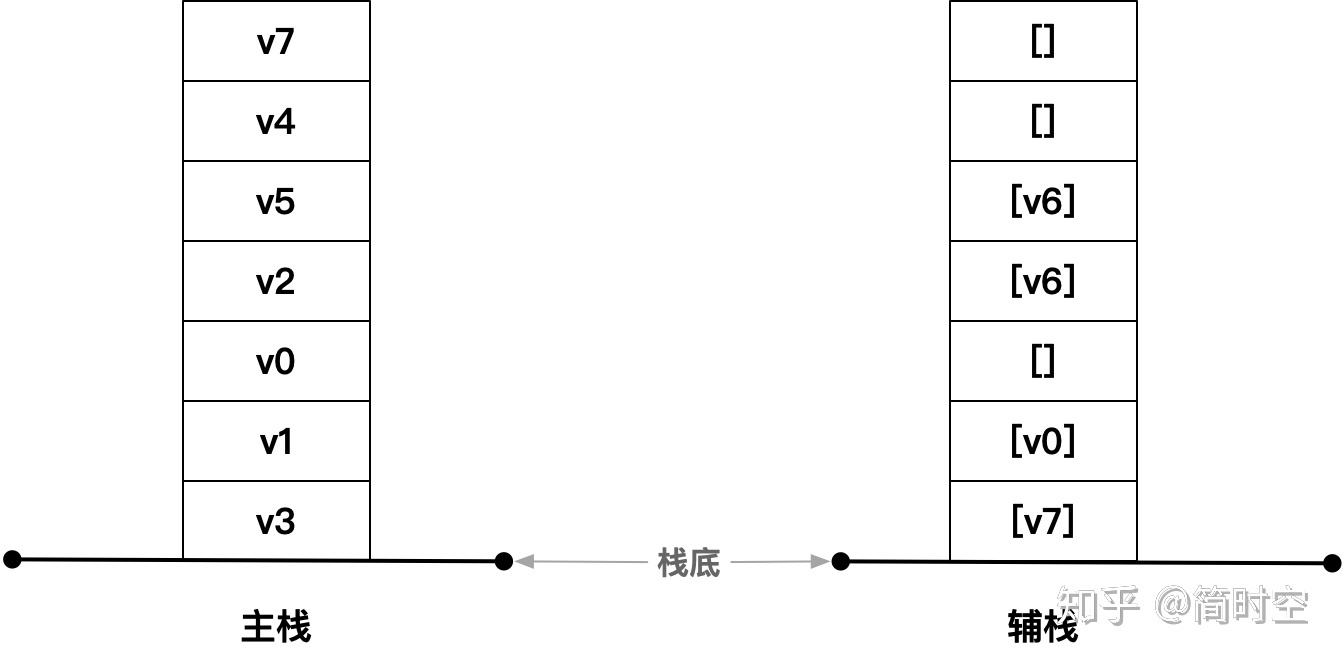
由于辅栈的栈顶是空列表 [],所以没法继续建栈了 —— 这表明这条路径走到尽头了都还没找到目标节点 v6。
走到 此路不通 的境地,我们就需要开始回退,看看来时的路上的其他岔路。
我们将主栈栈顶的 v7 弹出,同时也将辅栈的空列表 [] 弹出:
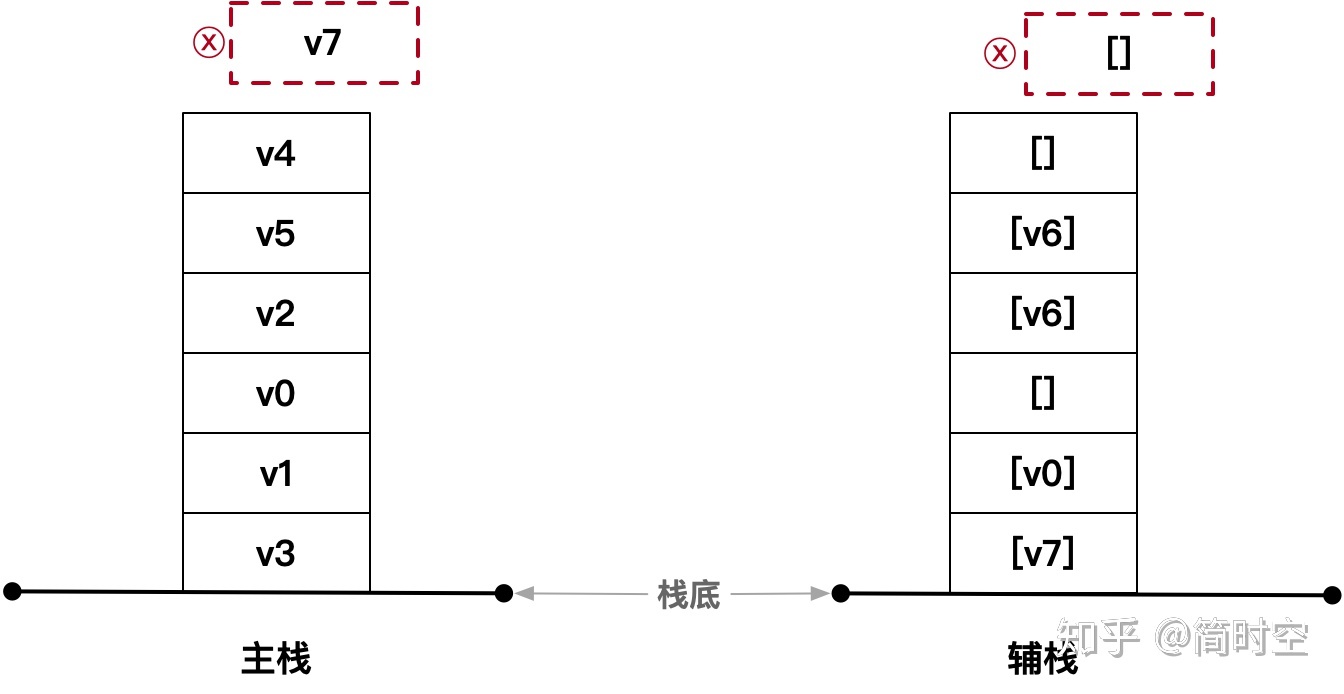
这一操作将导致 主栈 和 辅栈 长度减少,该过程我个人称之为 削栈(cutdown stack)。
Step 4:获取第一条路径
重复上述的 Step 2、Step 3,采取策略:
- 只要辅栈栈顶是非空列表,我们就建栈
- 只要辅栈栈顶是空列表,我们就削栈
直到主栈的顶部节点是目标节点 v6:

进行到这里,我们停下来观察一番,发现主栈里的内容已经是一条完整的从 v3 到 v6 的路径了:
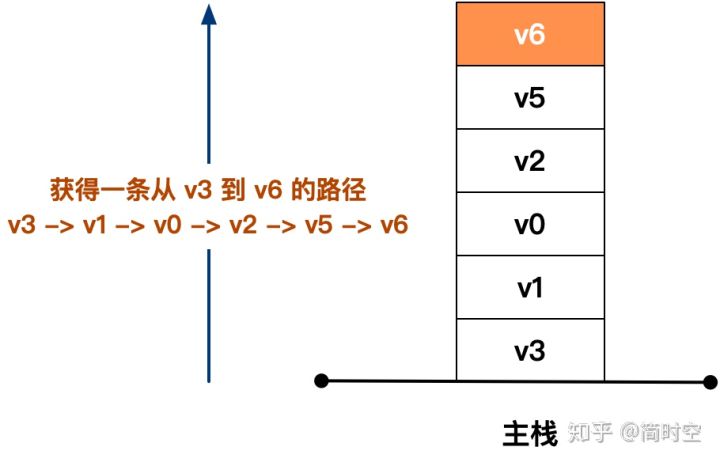
我们输出当前栈为数组:['v3', 'v1', 'v0', 'v2', 'v5', 'v6'],该数组就表示 v3 -> v1 -> v0 -> v2 -> v5 -> v6 这条路径。
进行至此,我们终于获取了一条从 v3 到 v6 的路径。
应该为自己的努力鼓个掌,已经看到胜利的曙光;接下来加个简单的循环就能获取所有的路径。
Step 5: 获取所有路径
重复 Step 2 - Step 4 步骤,采取策略如下:
- 只要辅栈栈顶是非空列表,我们就建栈
- 只要辅栈栈顶是空列表,我们就削栈
- 只要主栈栈顶是目标节点,我们输出路径,同时削栈
重复以上过程,直到主栈为空为止。
随着 建栈(build stack) 和 削栈(cutdown stack) 过程的进行,主栈和辅栈不断变化着,在这个变化的过程中我们就能不断地获取从 v3 到 v6 的路径,最终就可以获取所有的路径。
2、代码实现
2.1、伪代码
依据上述过程的描述,很方面将文字转换成伪代码:
BEGIN
初始化主栈
初始化辅栈
首次建栈
WHILE 主栈不为空 THEN
获取辅栈栈顶,为邻接节点列表
IF 邻接节点列表不为空 THEN
获取邻接节点列表首个元素
将该元素压入主栈,剩下列表压入辅栈
建栈
ELSE
削栈
CONTINUE
END IF
IF 主栈栈顶元素 === 目标节点 THEN
获取一条路径,保存起来
削栈
END IF
END WHILE
END
以上是我们拿无向图来做范例,实际上该算法也适合有向图。
总结
最近在复习 “图” 这数据结构,在过程中逐步尝试书写代码去实现个中算法。能够体会得到知识点只有经过自己思考和总结后,才能为之后的融会贯通打下基础。
在本文的学习总结中,有两点体会印象较为深刻:
- 能用能递归解决的问题,一般都可以用 循环 + 栈(Stack) 的方式来解决。
- 当不知道算法如何实现的时候,比较适合归纳总结的学习方法,即先逐步从简单场景开始演示,等摸索到其中规律之后再着手去实现。