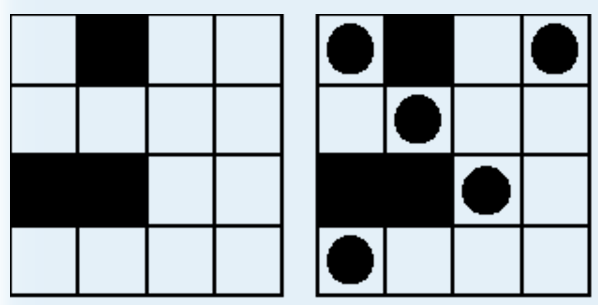
左边白方格里放小球,满足同一行、列只有一个(被黑块隔开)。问最多放多少个球。
------------------------------------------------------------------------------------------------------------
从贪心类别看到这个题的,读完题后只能想到枚举的解法 ==。智商有限。
看了题解后才知道怎么贪心,还有一个最大二分匹配的解法。
1.枚举
依次判断每个格子能不能放小球,如果能则返回 max{dfs(放),dfs(不放)},否则返回dfs(不放).
#define _CRT_SECURE_NO_DEPRECATE #include <set> #include <map> #include <stack> #include <queue> #include <cmath> #include <vector> #include <string> #include <cstdio> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> #define MAX(a,b) ((a)>=(b)?(a):(b)) #define MIN(a,b) ((a)<=(b)?(a):(b)) #define OO 0x0fffffff typedef long long LL; using namespace std; typedef pair<int, int> int2; const int dir[4][2] = { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 } }; char status[8][8]; int2 dots[16]; int dotcnt; int n; int dfs(int depth){ if (depth == dotcnt){ int ret = 0; for (int i = 0; i<n; i++) for (int j = 0; j<n; j++) if (status[i][j] == '*') ret++; return ret; } int x = dots[depth].first; int y = dots[depth].second; bool flag = true; for (int i = 0; i<4; i++){ for (int j = 1; flag; j++){ int tx = x + dir[i][0] * j; int ty = y + dir[i][1] * j; if (tx<0 || ty<0 || tx >= n || ty >= n) break; if (status[tx][ty] == 'X') break; if (status[tx][ty] == '*') { flag = false; break; } } } int no = dfs(depth + 1); if (flag) { status[x][y] = '*'; int yes = dfs(depth + 1); status[x][y] = '.'; return max(no,yes); } else return no; } int main(){ while (scanf("%d", &n), n){ dotcnt = 0; for (int i = 0; i<n; i++) { scanf("%s", status[i]); for (int j = 0; j<n; j++) if (status[i][j] != 'X') dots[dotcnt++] = make_pair(i, j); } printf("%d ", dfs(0)); } return 0; }
2. 贪心
统计每个白块所在行和列的连通区域的面积s,从第一排开始处理,找到s最小的块,标记,继续找第一排中最小的,如果没有了则挪到下一排。
3. 二分匹配
现在还没复习到二分图,只写一下二分图的构造:
a. 列收缩。所有列中每一个联通的白块看做一个点。记该序列为A;
b. 行收缩。得到序列B;
c. 连边。对所有(a,b)属于(A,B),如果ab相交则连一条边
接下来就是最大二分匹配了