证据权模型(C#版)

    证据权法是通过计算和利用各种不同证据的权重（表示相对重要性）并将多种证据结合起来，预测某个时间是否会发生的一种方法

    证据权法以概率论中的贝叶斯定理为基础。设D表示要一个随机事件。用P(D)表示这一事件概率，即D发生的概率。假设P(D)事先知道，即它是先验概率。则D不发生的概率为：

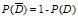
    定义：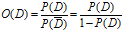

    称为事件D的几率(Odd Ratio)，也称优势率，它能更好的表示事件D发生的可能性大小。

    用集合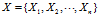

表示与D有关的n个证据，并设X_j都是逻辑变量。用D|X表示"单元中存在X的情况下D发生"这一事件。用P(D|X)表示概率，也称为后验概率（后验概率是获得有关信息后对先验概率修正后的概率）。由贝叶斯定理：

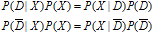
    可以得出优势率：

    假设n个条件相互条件独立，并在两边同时去对数：

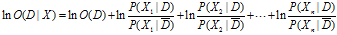
    令：

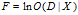
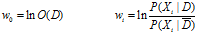
于是：

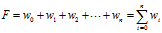
    事件D|X的几率为

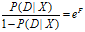
    于是后验概率为：

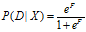
    其中w_i称为证据X的证据权，反应X_i的存在对D的重要性：

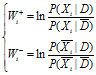
其中，各条件概率的计算：

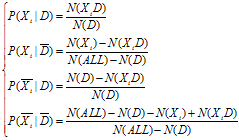
    定义：

    为X的对比系数，可以用来综合评价各证据的重要性

    在数据较少的情况下，采用C来选择证据，回增大结果的不确定性，定义

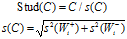
    其中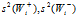：为第i个证据后验概率的正负方差：

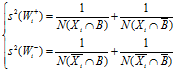
1.     /// <summary>
2. /// 计算先验似然概率
3. /// </summary>
4. private void GetMinePriorLikelihoodProb()
5. {
6.     mineral_PriorProbability = sum_EvidenceCount[0] / (double)gridNumber;
7.     minreal_PriorLiklihoodProbablity = mineral_PriorProbability / (1 - mineral_PriorProbability);
8. }
9. /// <summary>
10.        /// 计算证据权参数
11.        /// </summary>
12.        private void GetEvidenceStatistc()
13.        {
14.            for (int i = 0; i < mineral_EvidenceCount - 1; i++)
15.            {
16.                //证据权正定义
17.                /* Count(BjD)/Count(D)
18.                 * ln----------------------
19.                 * Count(Bj~D)/Count(~D)
20.                 */
21.                evidence_PosWeight[i] = Math.Log((sumEvidence_MineralOccur[i] / sum_EvidenceCount[0]) /
22.                    ((sum_EvidenceCount[i + 1] - sumEvidence_MineralOccur[i]) / (gridNumber - sum_EvidenceCount[0])));
23.  
24.                //证据权负定义
25.                /* Count(~BjD)/Count(D)
26.                 * ln-------------------------
27.                 * Count(~Bj~D)/Count(~D)
28.                 */
29.                evidence_NegWeight[i] = Math.Log(((sum_EvidenceCount[0] - sumEvidence_MineralOccur[i]) / (sum_EvidenceCount[0]))
30.                    / ((gridNumber - sum_EvidenceCount[0] - sum_EvidenceCount[i + 1] + sumEvidence_MineralOccur[i]) / (gridNumber - sum_EvidenceCount[0])));
31.  
32.                //证据权正方差
33.                /* 1 1
34.                 * -----------+--------------
35.                 * Count(BjD) Count(Bj~D)
36.                 */
37.                evidence_PosVariance[i] = (1 / sumEvidence_MineralOccur[i]) +
38.                    (1 / (sum_EvidenceCount[i + 1] - sumEvidence_MineralOccur[i]));
39.  
40.                //证据权负方差
41.                /* 1 1
42.                 * -----------+--------------
43.                 * Count(~BjD) Count(~Bj~D)
44.                 */
45.                evidence_NegVariance[i] = (1 / (sum_EvidenceCount[0] - sumEvidence_MineralOccur[i])) +
46.                    (1 / (gridNumber - sum_EvidenceCount[0] - sum_EvidenceCount[i + 1] + sumEvidence_MineralOccur[i]));
47.  
48.                //对比度
49.                //Cj=weightj+ - Weightj-
50.                evidence_ContrastRatio[i] = evidence_PosWeight[i] - evidence_NegWeight[i];
51.  
52.                //显著性统计量
53.                //Stud(C)=Cj/s(c)
54.                //s(c)=1/Sqrt(s2(weight+)+s2(weight-))
55.                evidence_StatisticalSignficance[i] = evidence_ContrastRatio[i] /
56.                    (Math.Sqrt(evidence_PosVariance[i] + evidence_NegVariance[i]));
57.            }
58.        }
59. /// <summary>
60.         /// 证据权合成
61.         /// </summary>
62.         private void SynthesisEvidence()
63.         {
64.             double[] evidence_PostProbLog = new double[gridNumber];
65.  
66.             double[,] evidence_Data = (double[,])mineralAndEvidence.Clone();
67.             for (int i = 1; i < mineral_EvidenceCount; i++)
68.             {
69.                 for (int j = 0; j < mineralAndEvidence.GetLength(1); j++)
70.                 {
71.                     //将复制证据图层中与对调
72.                     if (evidence_Data[i, j] == 0)
73.                     {
74.                         evidence_Data[i, j] = 1;
75.                     }
76.                     else
77.                     {
78.                         evidence_Data[i, j] = 0;
79.                     }
80.                     evidence_PostProbLog[j] += evidence_Data[i, j] * evidence_NegWeight[i - 1] +
81.                         mineralAndEvidence[i, j] * evidence_PosWeight[i - 1];
82.                 }//for
83.             }//for
84.             GetPostProb(evidence_PostProbLog);
85.         }//Method End
86. /// <summary>
87.         /// 计算后验概率
88.         /// </summary>
89.         /// <param name="postProbLog"></param>
90.         private void GetPostProb(double[] postProbLog)
91.         {
92.             evidence_PostProb = new double[gridNumber];
93.             for (int i = 0; i < postProbLog.Length; i++)
94.             {
95.                 evidence_PostProb[i] = (Math.Exp(postProbLog[i] + Math.Log(minreal_PriorLiklihoodProbablity)))
96.                     / (1 + Math.Exp(postProbLog[i] + Math.Log(minreal_PriorLiklihoodProbablity)));
97. }//for
98.         }