kmp算法专题

kmp算法前置技能：无

kmp算法是一种高效的字符串匹配算法，对于在给定长为n的主字符串S里查找长为m的模式字符串P，可以将时间复杂度从O(n*m)优化为O(n+m)。

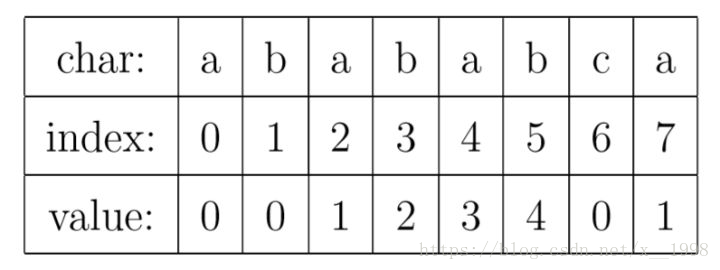
kmp算法的核心是一个被称为部分匹配表(Partial Match Table)(下文简称为PMT)的数组。对于一个字符串“abababca”来说，它的PMT如下图的value所示，PMT的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。

在主字符串S=“ababababca”中查找匹配字符串P=“abababca”。如果在j处字符不匹配，那么由于前面所说的匹配字符串PMT的性质，主字符串中i指针之前的PMT[j-1]位就一定与匹配字符串的第0位至第PMT[j-1]位是相同的。

以图中的例子来说，在i处失配，那么主字符串和匹配字符串的前6位就是相同的。又因为匹配字符串的前6位，它的前4位前缀和后4位后缀是相同的，所以我们推知主字符串，i之前的4位和匹配字符串开头的4位是相同的。就是图中的灰色部分，那这部分就不用比较了。

有了前面的思路，我们就可以使用PMT加速字符串的查找了。如果是在j位失配，那么影响j指针回溯的位置其实是第j-1位的PMT值，所以为了方便，我们不直接使用PMT数组，而是将PMT数组向后移一位。我们把新得到的这个数组称为next数组。

在上面的例题中，next数组如下图所示。其中我们在把PMT向后移的过程中，第0位的值我们设为-1，目的是便于编程。

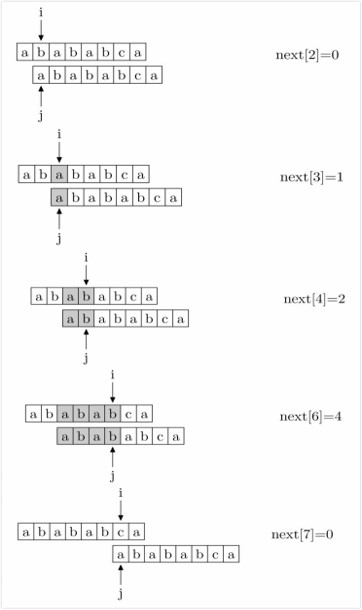
其实，求next数组的过程完全可以看成字符串匹配的过程，即以匹配字符串为主字符串，以匹配字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度。具体来说，就是从匹配字符串的第1位(注意，不包括第0位)开始对自身进行匹配运算。在任一位置，能匹配的最长长度就是当前位置的next值，如下图所示。

例题：
HDU1711 Number Sequence

Problem Description
Given two sequences of numbers: a[1], a[2], ...... , a[N], and b[1], b[2], ...... , b[M] (1 <= M <= 10000, 1 <= N <= 1000000). Your task is to find a number K which make a[K] = b[1], a[K + 1] = b[2], ...... , a[K + M - 1] = b[M]. If there are more than one K exist, output the smallest one.

Input
The first line of input is a number T which indicate the number of cases. Each case contains three lines. The first line is two numbers N and M (1 <= M <= 10000, 1 <= N <= 1000000). The second line contains N integers which indicate a[1], a[2], ...... , a[N]. The third line contains M integers which indicate b[1], b[2], ...... , b[M]. All integers are in the range of [-1000000, 1000000].

Output
For each test case, you should output one line which only contain K described above. If no such K exists, output -1 instead.

Sample Input
2
13 5
1 2 1 2 3 1 2 3 1 3 2 1 2
1 2 3 1 3
13 5
1 2 1 2 3 1 2 3 1 3 2 1 2
1 2 3 2 1

Sample Output
6
-1

参考代码：

#include <stdio.h>
#include <string.h>

int n, m;
int a[1000005], b[10005], next[10005];

void buildnext()
{
    next[0] = -1;
    int i = 0, j = -1;
    while (i < m)
    {
        if (j == -1 || b[i] == b[j])
            next[++i] = ++j;
        else
            j = next[j];
    }
}

int kmp()
{
    buildnext();
    int i = 0, j = 0;
    while (i < n && j < m)
    {
        if (j == -1 || a[i] == b[j])
        {
            ++i;
            ++j;
        }
        else
            j = next[j];
    }
    if (j == m)
        return i - j;
    else
        return -1;
}

int main()
{
    int t, i, ret;
    scanf("%d", &t);
    while (t--)
    {
        memset(a, 0, sizeof(a));
        memset(b, 0, sizeof(b));
        memset(next, 0, sizeof(next));
        scanf("%d %d", &n, &m);
        for (i = 0; i < n; ++i)
            scanf("%d", &a[i]);
        for (i = 0; i < m; ++i)
            scanf("%d", &b[i]);
        ret = kmp();
        if (ret >= 0)
            printf("%d
", ret + 1);
        else
            printf("-1
");
    }
    return 0;
}

参考资料：https://www.zhihu.com/question/21923021/answer/281346746