先来看看书中的定义:


然后了解一些有关图的其他定义:
-
图中的数据元素称为顶点(链表中称为元素)
-
强调顶点有穷非空
-
任意两个顶点可能都有关系,顶点之间的关系用边来表示
-
无向边和无向图
-
有向边(弧)和有向图
-
无向完全图和有向完全图
-
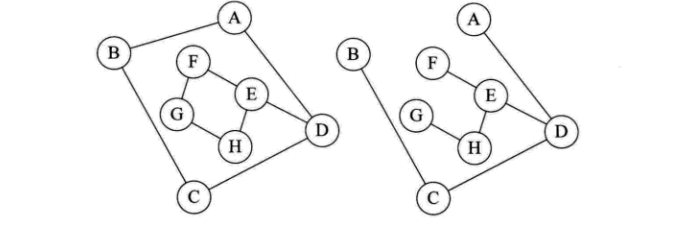
连通图(下右图为连通图)

- 生成树:一个极小的连通子图,它含有图中所有顶点,但只有构成一棵树的n-1条边
存储结构
-
邻接矩阵:即二维数组,用来存储顶点信息和边的信息(浪费空间)
-
邻接表(逆邻接表):使用一个一维数组存储顶点信息,然后将每个顶点的边用链表存储

- 十字链表(将邻接表和逆邻接表整合在一起)

- 邻接多重表(针对无向图的优化):用一个结点表示一条边,邻接表中用俩个结点表示一条一条边

- 边集数组:使用两个一维数组,一个存储顶点数据,一个存储边的数据

图的遍历:
-
深度优先遍历
-
广度优先遍历
最小生成树:
-
普利姆算法(Prim)(根据顶点进行构建)
-
克鲁斯卡尔算饭(Kruskal)(根据边进行构建)
最短路径:
-
迪杰斯特拉算法(Dijkstra)
-
弗罗因德算法(Floyd)
拓扑排序
关键路径
结束语:
-
本章在这里也算是潦草的结束了吧,图这一章涉及了许多新概念,所以感觉比较难,而且后面介绍的一些算法,如Prim,Kruskal等,并不知道它们的用途在何方,实用性在何处,因此学习动力不是很强,也没有那种特别想要理解的渴望,所以暂时就这样了,以后遇到再深究。
-
总的来说,这章学的比较草率,过段时间再来一遍吧,哈哈!