树的定义:
- 书中是这样定义的:

-
在学习树之前,我们必须先要了解一些常用的术语(超级多+超级烦,有没有):
-
结点:树的结点包含一个数据元素及若干指向其子树的分支(使用"结点"而不使用"节点",据说是因为结点的语义更符合树的数据结构)
-
结点的度:结点拥有的子树数
-
叶结点:度为0的结点
-
根结点:树顶结点(仅有一个)
-
树的度:树内各结点度的最大值

-
结点之间的关系:
-
孩子
-
双亲
-
兄弟
-
子孙

-
-
树的其他相关概念:
-
结点的层次:从根开始定义,根为第一层,根的孩子为第二层
-
树的深度(高度):树种结点最大层次

-
-
有序树和无序树
-
与线性结构的比较:
-

树的抽象数据类型:

树的存储结构:(注:这里的“指针域”、“引用”、“下标”都是一个意思)
-
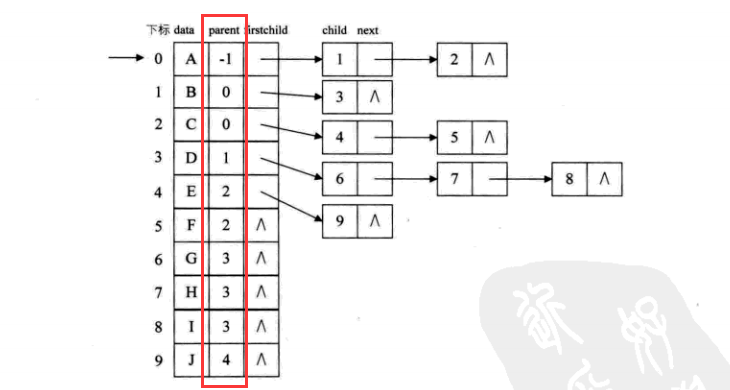
双亲表示法:
-
首先使用一个数组将所有元素存储起来
-
然后使用链表的形式,让每个结点存储其双亲结点的下标值(引用)即可
-
若需要方便找到孩子结点,还可存储结点最左边孩子(长子)的下标(引用,域)
-
还可以存储结点右兄弟的下标(引用)
-
寻找所有孩子结点时,即从长子开始,逐个遍历兄弟结点即可。但若没有存储右孩子的结点,需要判断右孩子的双亲是不是该结点。
-


-
孩子表示法:
-
与双亲表示法不同,因为每个结点的孩子结点有多个,而且每个结点的孩子数量不一定一致,因此需要存储的下标(引用)数量也不一样,书中给了两种解决方案:
- 方案一:每个结点的指针域个数=树的度(空间存在很大浪费,相比方案二更好)
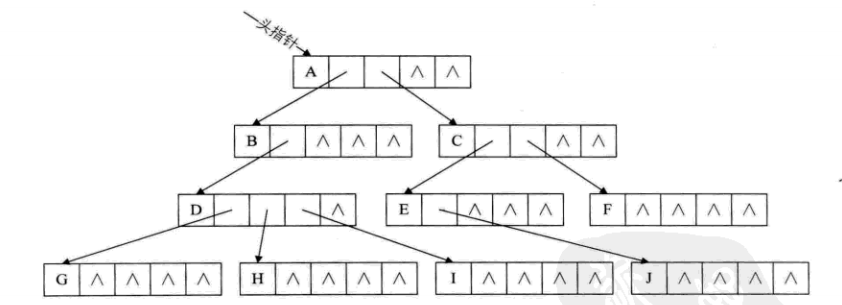
- 方案二:每个结点的指针域个数等于该结点的度,并单独取一个位置存储结点的指针域个数(结点的度)

- 方案一:每个结点的指针域个数=树的度(空间存在很大浪费,相比方案二更好)
-
对每个结点的孩子建立一个单链表(因为图上下对的比较齐,容易误解“单链表”,因此我用红色箭头标示出来了,一个红色箭头表示一“链表”)
-

- 双亲孩子表示法:
- 孩子兄弟表示法:
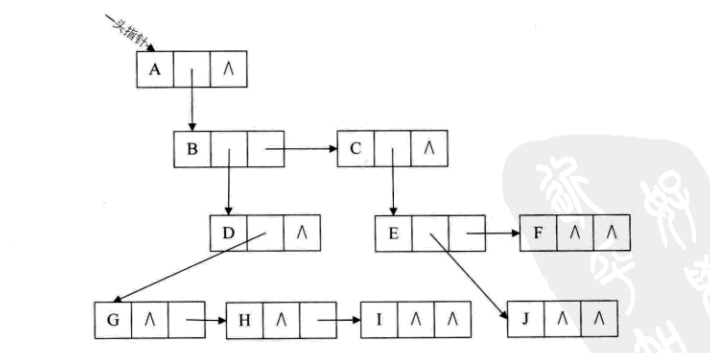
- 因为,因为这种存储结构的特点(每个结点存储一个长子和一个右兄弟结点),因此将复杂的树变成了一个二叉树

- 篇幅有点长了,下篇再说传说中的二叉树。