题目描述
现有一块大奶酪,它的高度为 h,它的长度和宽度我们可以认为是无限大的,奶酪 中间有许多 半径相同 的球形空洞。我们可以在这块奶酪中建立空间坐标系,在坐标系中, 奶酪的下表面为z=0,奶酪的上表面为z=h。
现在,奶酪的下表面有一只小老鼠 Jerry,它知道奶酪中所有空洞的球心所在的坐 标。如果两个空洞相切或是相交,则 Jerry 可以从其中一个空洞跑到另一个空洞,特别 地,如果一个空洞与下表面相切或是相交,Jerry 则可以从奶酪下表面跑进空洞;如果 一个空洞与上表面相切或是相交,Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道,在 不破坏奶酪 的情况下,能否利用已有的空洞跑 到奶酪的上表面去?
空间内两点P1(x1,y1,z1)、P2(x2,y2,z2)的距离公式如下:
dist(P1,P2)=sqrt((x1−x2)^2+(y1−y2)^2+(z1−z2)^2
输入输出格式
输入格式:
每个输入文件包含多组数据。
的第一行,包含一个正整数 T,代表该输入文件中所含的数据组数。
接下来是 T 组数据,每组数据的格式如下: 第一行包含三个正整数 n,h 和 r,两个数之间以一个空格分开,分别代表奶酪中空 洞的数量,奶酪的高度和空洞的半径。
接下来的 n 行,每行包含三个整数 x,y,z,两个数之间以一个空格分开,表示空 洞球心坐标为(x,y,z)。
输出格式:
T 行,分别对应 T 组数据的答案,如果在第 i 组数据中,Jerry 能从下 表面跑到上表面,则输出Yes,如果不能,则输出No (均不包含引号)。
输入输出样例
说明
【输入输出样例 1 说明】
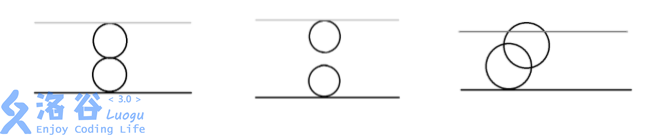
第一组数据,由奶酪的剖面图可见:
第一个空洞在(0,0,0)与下表面相切
第二个空洞在(0,0,4)与上表面相切 两个空洞在(0,0,2)相切
输出 Yes
第二组数据,由奶酪的剖面图可见:
两个空洞既不相交也不相切
输出 No
第三组数据,由奶酪的剖面图可见:
两个空洞相交 且与上下表面相切或相交
输出 Yes
【数据规模与约定】
对于 20%的数据,n=1,1≤h , r≤10,000,坐标的绝对值不超过 10,000。
对于 40%的数据,1≤n≤8, 1≤h , r≤10,000,坐标的绝对值不超过 10,000。
对于80%的数据, 1≤n≤1,000, 1≤h,r≤10,000,坐标的绝对值不超过10,000。
对于 100%的数据,1≤n≤1,000,1≤h,r≤1,000,000,000,T≤20,坐标的 绝对值不超过1,000,000,000。
1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<algorithm> 5 using namespace std; 6 int T,i,j,n,op,fa[1005],ta = 0,to = 0,di[1005],gao[1005]; 7 long long int h,r; 8 struct node 9 { 10 long long int x; 11 long long int y; 12 long long int z; 13 }a[1005]; 14 int find(int x) 15 { 16 if(fa[x] != x) 17 { 18 fa[x] = find(fa[x]); 19 } 20 return fa[x]; 21 } 22 void lianjie(int x,int y) 23 { 24 x = find(x); 25 y = find(y); 26 fa[y] = x; 27 } 28 int main() 29 { 30 scanf("%d",&T); 31 for(i = 1;i <= T;i++) 32 { 33 op = 0; 34 to = 0; 35 ta = 0; 36 scanf("%d %lld %lld",&n,&h,&r); 37 for(j = 1;j <= n;j++) 38 { 39 fa[j] = j; 40 scanf("%lld %lld %lld",&a[j].x,&a[j].y,&a[j].z); 41 if(a[j].z - r <= 0) 42 { 43 to++; 44 di[to] = j; 45 } 46 if(a[j].z + r >= h) 47 { 48 ta++; 49 gao[ta] = j; 50 } 51 for(int k = 1;k <= j;k++) 52 { 53 if(sqrt((a[j].x - a[k].x) * (a[j].x - a[k].x) + (a[j].y - a[k].y) * (a[j].y - a[k].y) + (a[j].z - a[k].z) * (a[j].z - a[k].z)) <= r * 2) 54 { 55 lianjie(j,k); 56 } 57 } 58 } 59 for(j = 1;j <= ta;j++) 60 { 61 for(int k = 1;k <= to;k++) 62 { 63 if(find(di[k]) == find(gao[j])) 64 { 65 printf("Yes"); 66 op = 1; 67 break; 68 } 69 } 70 if(op == 1) 71 break; 72 } 73 if(op == 0) 74 printf("No"); 75 if(i != T) 76 printf(" "); 77 } 78 return 0; 79 }
*****这是一个并查集,从保存下来可以通往顶部和底部的点,找他俩的公共爸爸,如果是一个则证明是这条路是连通哒,每一次都要搜索这个点和他之前的那些点是否连通哦。