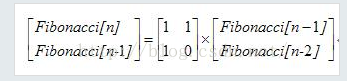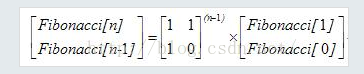- 恕我愚昧,今天才知道斐波拉契还可以这样解
- 源于上次快手的笔试题,本来以为很简单的斐波拉契结果总是时间超时
- 矩阵快速幂 精髓:比如A^19 => (A^16)*(A^2)*(A^1),显然采取这样的方式计算时因子数将是log(n)级别的(原来的因子数是n),不仅这样,因子间也是存在某种联系的,比如A^4能通过(A^2)*(A^2)得到,A^8又能通过(A^4)*(A^4)得到,这点也充分利用了现有的结果作为有利条件。下面举个例子进行说明:现在要求A^156,而156(10)=10011100(2) 也就有A^156=>(A^4)*(A^8)*(A^16)*(A^128) 考虑到因子间的联系,我们从二进制10011100中的最右端开始计算到最左端。
while(N) { if(N&1) res=res*A; N>>=1; A=A*A; }
例题:
//计算(x^y) % N; 注:(x^y)表示x的y次方 #if 0 int main() { int x, y, N; cin >> x >> y >> N; long res = 1; x = x % N; //开始 while (y > 0) { if (y % 2 == 1) //等价于 if(y&1) res = (res * x) % N; y /= 2; //y>>1; 分解y为二进制编码 x = (x * x) % N; } cout << res << endl; return 0; } #endif
对于矩阵乘法与递推式之间的关系:
In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
如:在斐波那契数列之中
f[i] = 1*f[i-1]+1*f[i-2] f[i-1] = 1*f[i-1] + 0*f[i-2];即
所以:
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 7241 | Accepted: 5131 |
Description
In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
An alternative formula for the Fibonacci sequence is
 .
.
Given an integer n, your goal is to compute the last 4 digits of Fn.
Input
The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.
Output
For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).
Sample Input
0 9 999999999 1000000000 -1
Sample Output
0 34 626 6875
Hint
As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by
 .
.
Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:
 .
.
Source
#if 1 #include <cstdio> #include <iostream> using namespace std; const int MOD = 10000; struct matrix { int m[2][2]; }ans, base; matrix multi(matrix a, matrix b) { matrix tmp; for(int i = 0; i < 2; ++i) { for(int j = 0; j < 2; ++j) { tmp.m[i][j] = 0; for(int k = 0; k < 2; ++k) tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % MOD; } } return tmp; } int fast_mod(int n) // 求矩阵 base 的 n 次幂 { base.m[0][0] = base.m[0][1] = base.m[1][0] = 1; base.m[1][1] = 0; ans.m[0][0] = ans.m[1][1] = 1; // ans 初始化为单位矩阵 ans.m[0][1] = ans.m[1][0] = 0; while (n) { if (n & 1) //实现 ans *= t; 其中要先把 ans赋值给 tmp,然后用 ans = tmp * t { ans = multi(ans, base); } base = multi(base, base); n >>= 1; } return ans.m[0][1]; } int main() { int n; while (scanf("%d", &n) && n != -1) { printf("%d ", fast_mod(n)); } return 0; } #endif