美团点评2017秋招笔试编程题

题目1

• 大富翁游戏，玩家根据骰子的点数决定走的步数，即骰子点数为1时可以走一步，点数为2时可以走两步，点数为n时可以走n步。求玩家走到第n步（n<=骰子最大点数且是方法的唯一入参）时，总共有多少种投骰子的方法。
• 归纳：f(n) = f(n-1)+f(n-2)+f(n-3)+....+f(1)+1，f(1)=1,f(2)=2.则f(n)=2^(n-1).

题目2

• 给你六种面额 1、5、10、20、50、100 元的纸币，假设每种币值的数量都足够多，编写程序求组成N元（N为0~10000的非负整数）的不同组合的个数。

题目3

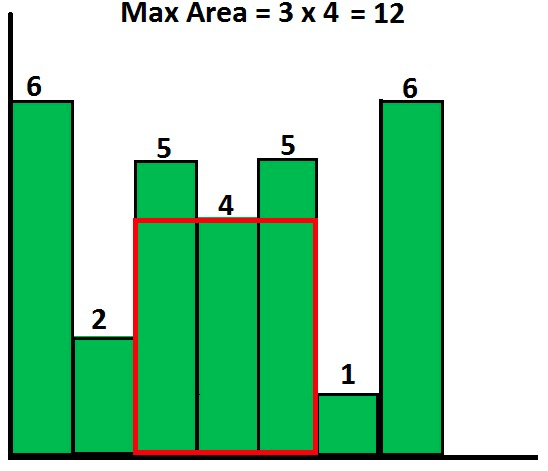
• 给定一组非负整数组成的数组h，代表一组柱状图的高度，其中每个柱子的宽度都为1。 在这组柱状图中找到能组成的最大矩形的面积（如图所示）。 入参h为一个整型数组，代表每个柱子的高度，返回面积的值。
• 

题目4

• 给出两个字符串（可能包含空格）,找出其中最长的公共连续子串,输出其长度。

AC代码

#include<iostream>
#include<math.h>

#include <vector>
#include <string>
#include <deque>
#include <stack>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
#include <unordered_set>

#include <algorithm>
#include <functional>
#include <numeric> //accmulate

using namespace std;


int GetLongestComSub(string str1,string str2)
{
	int m = str1.size();
	int n = str2.size();

	vector<vector<int >> vecs(m + 1, vector<int>(n + 1, 0));
	int max_len = 0;

	for (int i = 0; i < m;i++)
	{
		for (int j = 0; j < n;j++)
		{
			if (str1[i]==str2[j])
			{
				vecs[i + 1][j + 1] = vecs[i][j]+1;
				if (max_len<vecs[i+1][j+1])
				{
					max_len = vecs[i+1][j+1];
				}
			}
		}
	}

	return max_len;
}
//
//测试用例:
//Sit it out G
//Sit down and shut up

//cin输入字符串的总结：
//
//遇空字符（包括空格、回车、TAB）表示一个输入的结束，连续的空字符会被忽略。
int main()
{
	string str1, str2;
	/*cin >> str1;
	cin >> str2;*/
	getline(cin, str1);
	getline(cin, str2);

	cout<<GetLongestComSub(str1,str2)<<endl;

	return 0;
}



int  GetMaxRect(vector<int>& vec)
{
	int max_area = vec[0];

	for (int i = 1; i < vec.size();i++)
	{
		int low = i - 1, high = i + 1;
		while (low >= 0 && vec[i] <= vec[low])
	        low--;	
		while (high<vec.size() && vec[i] <= vec[high])
			high++;
			
		max_area = max(max_area, vec[i] * (high - low-1));
	}

	return max_area;
}

int main()
{
	int n;
	cin >> n;
	vector<int> vec;
	int temp = 0;
	for (int i = 0; i < n;i++)
	{
		cin >> temp;
		vec.push_back(temp);
	}

	cout << GetMaxRect(vec) << endl;

	return 0;
}


int main()
{
	int n;
	cin >> n;

	int table[] = { 1, 5, 10, 20, 50, 100 }; //6种面额
	//数字很大时，int表示不够  
	vector<vector<long long>> dp(sizeof(table) / sizeof(int), vector<long long>(n + 1, 0)); //dp[i][j]表示用前（i+1）中面额组合成j面额的方法数
	for (int j = 0; j <= n; j++)
	{
		dp[0][j] = 1;
	}
	for (int i = 1; i < 6; i++)
	{
		for (int j = 0; j <= n; j++)
		{
			for (int k = 0; k <= j / table[i]; k++) //j=0时，dp[i][j] = dp[i - 1][j]
			{
				dp[i][j] += dp[i - 1][j - k*table[i]];
			}
		}
	}

	cout << dp[5][n] << endl;
	return 0;
}

/*动态规划
需要拼凑的面额是n，
维护dp[i],表示取到i时的组合数目，dp[0]=1，
面额数组a[6]={1,5,10,20,50,100}，
dp[j]=dp[j]+dp[j-a[i]],约数条件j>a[i]。
因为面额数目任意，所以需要分别处理只有面额1时，组合钱数为1~n的各自组合数dp[1]~dp[n],
然后有面额1,5时，组合钱数为1~n的各自组合数dp[1]~dp[n],依此内推。。。详情见程序。
*/
#include<iostream>  
#include<vector>  
using namespace std;

int main()
{
	int n;
	cin >> n;
	int a[6] = { 1, 5, 10, 20, 50, 100 };
	vector<long> dp(n + 1, 0);   //当数字很大时，int表示不够  
	dp[0] = 1;
	for (int i = 0; i < 6; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			if (j >= a[i])
				dp[j] = dp[j] + dp[j - a[i]];   //j值取和不取两种情况组合数目之和  
		}
	}
	cout << dp[n] << endl;
	return 0;
}

int main()
{
	int n;
	cin >> n;
	
	int* fn = new int[n];
	fn[0] = 1;
	fn[1] = 2;
	
	for (int i = 2; i < n;i++)
	{
		int ret = 0;
		for (int j = 0; j < i;j++)
		{
			ret += fn[j];
		}
		fn[i] = ret + 1;
	
	}
	cout << fn[n - 1] << endl;
	return 0;
}