题目链接:https://www.acwing.com/problem/content/215/
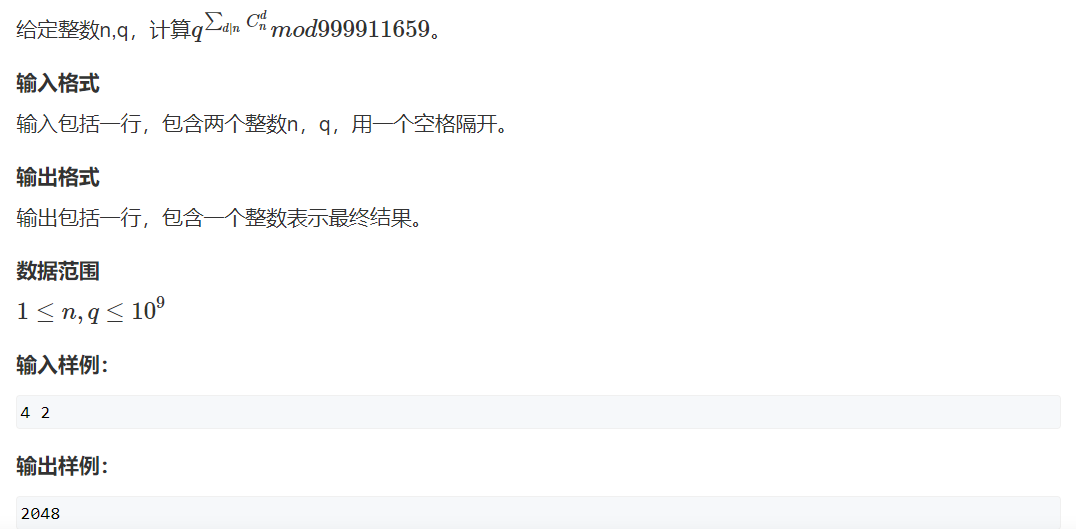
通过欧拉定理推论可以知道这个公式的计算可以变成对指数%(mod-1)的计算,涉及到组合数取模的问题,遂考虑卢卡斯定理,由于模数不是质数,考虑分解质因数,发现是一个square free number,可以通过模线性方程组来求解这个最小的指数x,求最小的正整数x是因为,如果指数是k*(mod-1)+x的话,根据费马小定理,q^(k*(mod-1))=1%(mod),对结果没有贡献。
求解过程用到了Lucas定理,和对不同的模质数进行取模。逆元可以用exgcd或者费马小定理在O(logn)时间内求解。
代码:
#include<iostream> #include<cstdio> using namespace std; typedef long long ll; const ll mod=999911659; ll p[5]={0,2,3,4679,35617},m[5]={0},t[5]; ll pn[5][35620][2];//0存放对应的阶乘取模,1存放阶乘的逆元 ll ksm(ll a,ll b,ll mod){ ll ans=1; a%=mod; b%=(mod-1);//费马小定理 while(b){ if(b&1)ans=(ans*a)%mod; a=(a*a)%mod; b>>=1; } return ans; } ll C(ll n,ll d,ll i){//lucas定理求组合数取模 ,使用第i个模数 if(d<p[i] && n<p[i])return pn[i][n][0]*pn[i][d][1]%p[i]*pn[i][n-d][1]%p[i]; return C(n%p[i],d%p[i],i)*C(n/p[i],d/p[i],i)%p[i]; } int main(){ ll n,q; cin>>n>>q; if(q==mod){ cout<<"0"<<endl; return 0; } for(int i=1;i<=4;i++)pn[i][0][0]=pn[i][0][1]=pn[i][1][0]=pn[i][1][1]=1; for(int i=2;i<=4;i++){ for(int j=2;j<p[i];j++){ pn[i][j][0]=pn[i][j-1][0]*j%p[i];//阶乘对应取模 pn[i][j][1]=ksm(pn[i][j][0],p[i]-2,p[i]); } } for(int i=1;i<=4;i++){ m[i]=(mod-1)/p[i]; t[i]=ksm(m[i],p[i]-2,p[i]); } ll a[5]={0,0,0,0,0}; for(int d=1;d*d<=n;d++){//分解质因数 if(n%d==0){ for(int i=1;i<=4;i++){ a[i]=(a[i]+C(n,d,i))%p[i]; if(d*d!=n)a[i]=(a[i]+C(n,n/d,i))%p[i]; } } } ll ans=0; for(int i=1;i<=4;i++){//中国剩余定理 ans=(m[i]*a[i]%(mod-1)*t[i]%(mod-1)+ans)%(mod-1); } ans=(ans+mod-1)%(mod-1);//求得指数 cout<<ksm(q,ans,mod)<<endl; return 0; }