朴素线性回归的实现,直接通过梯度为0解出w的估计值
import numpy as np class OLSLinearRegression: def _ols(self, X, y): '''最小二乘法估算w''' # tmp = np.linalg.inv(np.matmul(X.T, X)) # tmp = np.matmul(tmp, X.T) # return np.matmul(tmp, y) # 若使用较新的python和numpy版本, 可使用如下实现. return np.linalg.inv(X.T @ X) @ X.T @ y def _preprocess_data_X(self, X): '''数据预处理''' # 扩展X, 添加x0列并置1. m, n = X.shape X_ = np.empty((m, n + 1)) X_[:, 0] = 1 X_[:, 1:] = X return X_ def train(self, X_train, y_train): '''训练模型''' # 预处理X_train(添加x0=1) X_train = self._preprocess_data_X(X_train) # 使用最小二乘法估算w self.w = self._ols(X_train, y_train) def predict(self, X): '''预测''' # 预处理X_train(添加x0=1) X = self._preprocess_data_X(X) return np.matmul(X, self.w)
一般梯度下降算法拟合参数
import numpy as np class GDLinearRegression: def __init__(self, n_iter=200, eta=1e-3, tol=None): # 训练迭代次数 self.n_iter = n_iter # 学习率 self.eta = eta # 误差变化阈值 self.tol = tol # 模型参数w(训练时初始化) self.w = None def _loss(self, y, y_pred): '''计算损失''' return np.sum((y_pred - y) ** 2) / y.size def _gradient(self, X, y, y_pred): '''计算梯度''' return np.matmul(y_pred - y, X) / y.size def _gradient_descent(self, w, X, y): '''梯度下降算法''' # 若用户指定tol, 则启用早期停止法. if self.tol is not None: loss_old = np.inf # 使用梯度下降至多迭代n_iter次, 更新w. for step_i in range(self.n_iter): # 预测 y_pred = self._predict(X, w) # 计算损失 loss = self._loss(y, y_pred) print('%4i Loss: %s' % (step_i, loss)) # 早期停止法 if self.tol is not None: # 如果损失下降不足阈值, 则终止迭代. if loss_old - loss < self.tol: break loss_old = loss # 计算梯度 grad = self._gradient(X, y, y_pred) # 更新参数w w -= self.eta * grad def _preprocess_data_X(self, X): '''数据预处理''' # 扩展X, 添加x0列并置1. m, n = X.shape X_ = np.empty((m, n + 1)) X_[:, 0] = 1 X_[:, 1:] = X return X_ def train(self, X_train, y_train): '''训练''' # 预处理X_train(添加x0=1) X_train = self._preprocess_data_X(X_train) # 初始化参数向量w _, n = X_train.shape self.w = np.random.random(n) * 0.05 # 执行梯度下降训练w self._gradient_descent(self.w, X_train, y_train) def _predict(self, X, w): '''预测内部接口, 实现函数h(x).''' return np.matmul(X, w) def predict(self, X): '''预测''' X = self._preprocess_data_X(X) return self._predict(X, self.w)
使用随机梯度下降的算法拟合参数:
import numpy as np class SGDLinearRegression: def __init__(self, n_iter=1000, eta=0.01): # 训练迭代次数 self.n_iter = n_iter # 学习率 self.eta = eta # 模型参数theta (训练时根据数据特征数量初始化) self.theta = None def _gradient(self, xi, yi, theta): # 计算当前梯度 return -xi * (yi - np.dot(xi, theta)) def _stochastic_gradient_descent(self, X, y, eta, n_iter): # 复制X(避免随机乱序时改变原X) X = X.copy() m, _ = X.shape eta0 = eta step_i = 0 for j in range(n_iter): # 随机乱序 np.random.shuffle(X) for i in range(m): # 计算梯度(每次只使用其中一个样本) grad = self._gradient(X[i], y[i], self.theta) # 更新参数theta step_i += 1 #eta = 4.0 / (1.0 + i + j) + 0.000000001 eta = eta0 / np.power(step_i, 0.25) self.theta += eta * -grad def train(self, X, y): if self.theta is None: _, n = X.shape self.theta = np.zeros(n) self._stochastic_gradient_descent(X, y, self.eta, self.n_iter) def predict(self, X): return np.dot(X, self.theta)
测试代码:
数据集的下载网址:
http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/
一、加载数据与数据展示:
import numpy as np data=np.genfromtxt(r'F:python_testdatawinequality-red.csv',delimiter=';',skip_header=True) X=data[:,:-1] print(X) #输出X展平之后的大小 print(X.size) #输出X的形状 print(X.shape) #结果集y y=data[:,-1] print(y) print(y.size)
结果:

二、划分测试集与训练集
from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) from keras.losses import mean_squared_error from sklearn.metrics import mean_absolute_error
三、使用朴素线性回归进行拟合
ols_lr=OLSLinearRegression() ols_lr.train(X_train,y_train) y_pred=ols_lr.predict(X_test) print('=========================朴素线性回归========================') print('在测试集上的预测结果:',y_pred) mse=mean_squared_error(y_test,y_pred) print('在30%的测试集上的均方误差mse:',mse) y_train_pred=ols_lr.predict(X_train) mse_train=mean_squared_error(y_train,y_train_pred) print('在70%地训练集上的均方误差mse:',mse_train) #计算平均绝对误差 mae=mean_absolute_error(y_test,y_pred) print('在30%的测试集上的平均绝对误差mae:',mae)
结果:

四、使用梯度下降算法拟合参数
gd_lr=GDLinearRegression(n_iter=3000,eta=0.0001,tol=0.00001) gd_lr.train(X_train,y_train) print(X.mean(axis=0))#观察每个属性的均值,发现相差过大,所以需要标准化处理
结果:
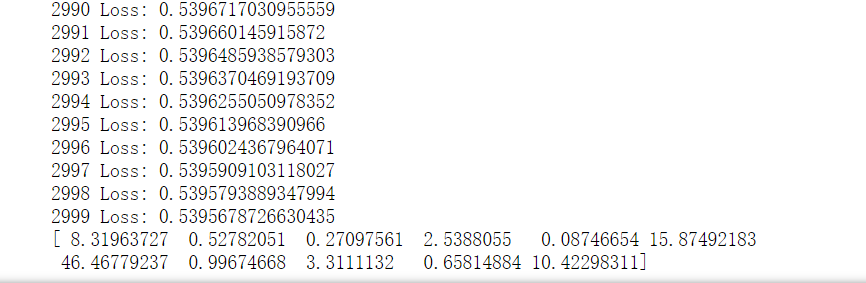
注意到损失函数并未收敛,并且属性的均值相差过大,需要进行标准化。学习率需要手动调整,防止震荡而无法收敛
五、使用标准化数据再次测试,在这里只是用训练集计算标准差以及均值
from sklearn.preprocessing import StandardScaler ss=StandardScaler() ss.fit(X_train)
结果:

查看训练集与测试集:
X_train_std=ss.transform(X_train) X_test_std=ss.transform(X_test) X_train_std[:3]

X_test_std

重新拟合参数:
gd_lr=GDLinearRegression(n_iter=3000,eta=0.05,tol=0.00001)
gd_lr.train(X_train_std,y_train)

可见137次之后便以及收敛到0.43,loss函数的值和之前朴素线性回归的值已经很接近
六、对测试集进行预测并且计算误差:
均方误差和OLS相比已经差不多了,平均绝对误差也是差不多了
y_pred=gd_lr.predict(X_test_std)
mse=mean_squared_error(y_test,y_pred)
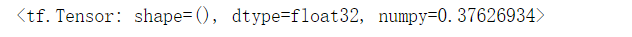
mae=mean_absolute_error(y_test,y_pred)
mae
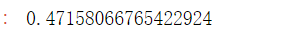
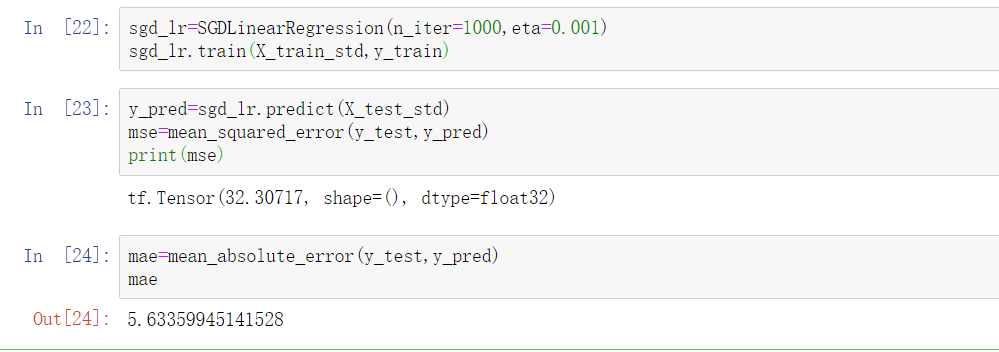
七、使用随机梯度下降算法进行计算
可见情况没有上述两种好