matlab解决线性规划问题

求解线性规划问题：

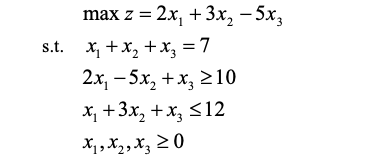
化为标准形式：

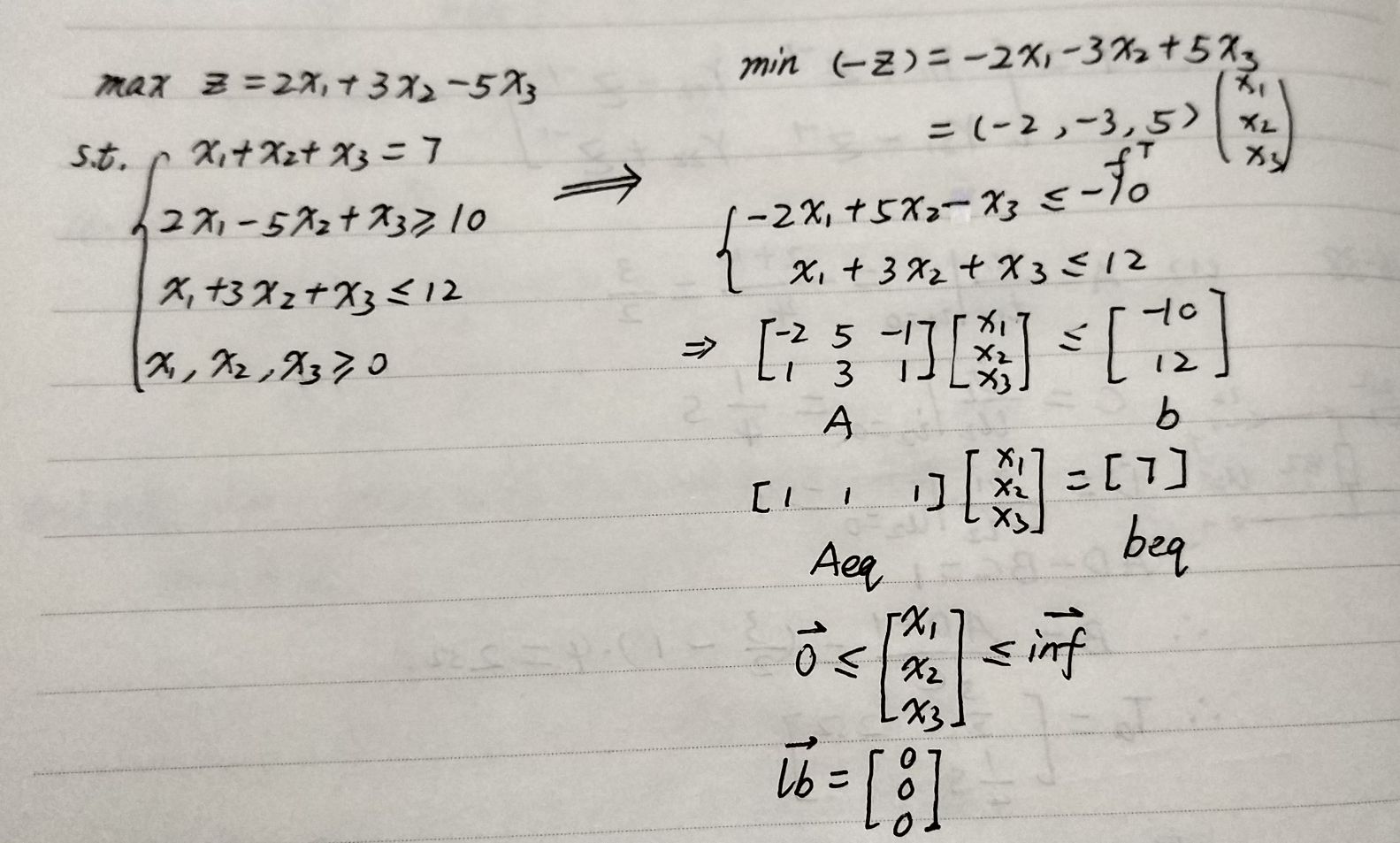
输入：

输出：

如果有非线性函数,如何做呢？

例如：

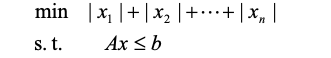
 每一个xi 变成了两个量 u, v 所以我们需要2n长度的向量来表示新的自变量x*，前n项为u，后n项为v；

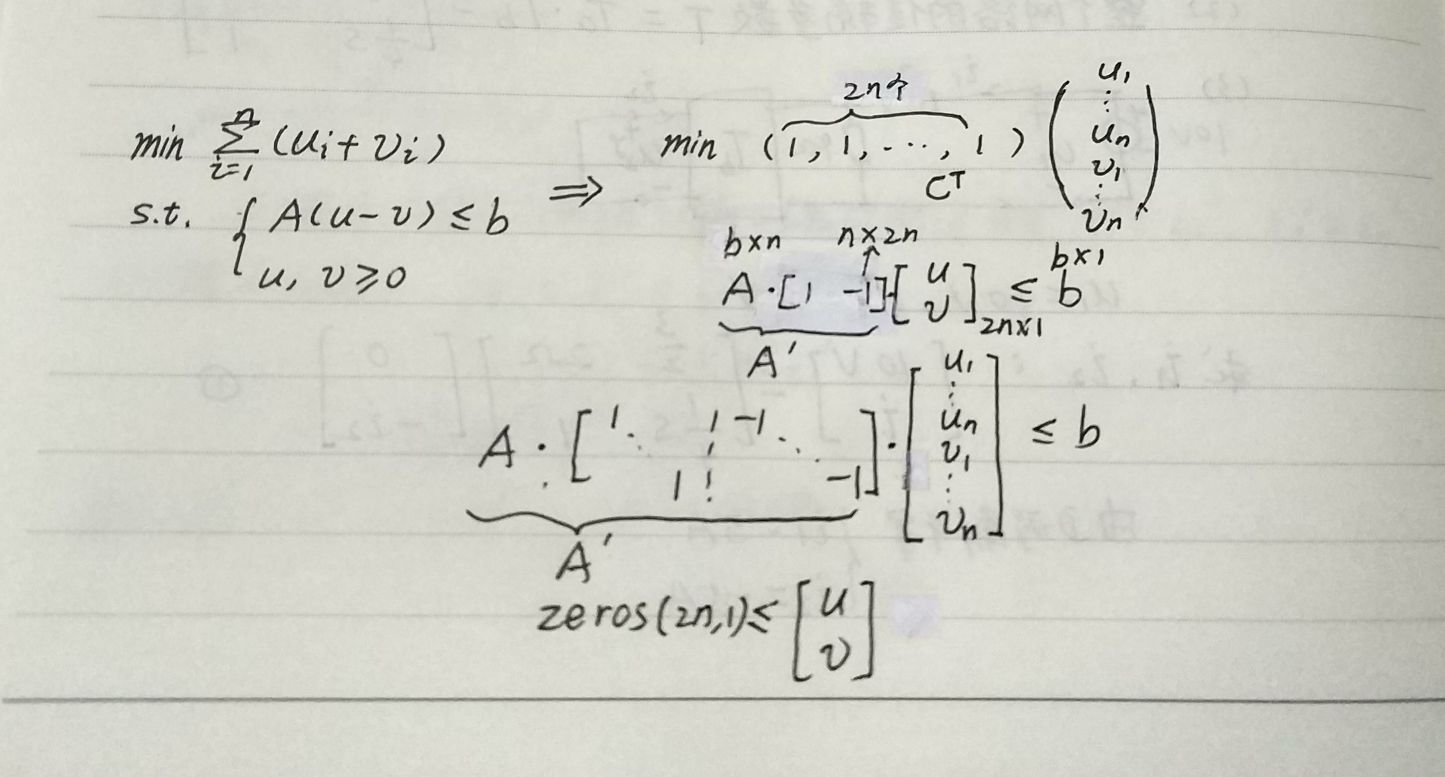
 如题：

 代码为：

c = 1:4;
c = [c,c]';
Aeq = [1 -1 -1 1;1 -1 1 -3;1 -1 -2 3];
beq = [0 1 -1/2]';
aeq = [Aeq,-Aeq];
[x,fval,exitflag] = linprog(c,[],[],aeq,beq,zeros(8,1))
x = x(1:4)-x(5:8)

输出为：

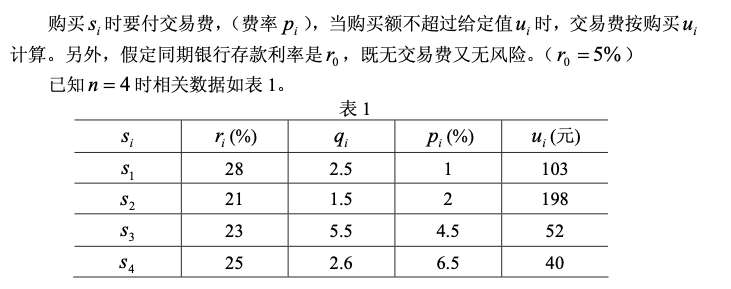
实际问题：

指派问题：

  

　　　　　　

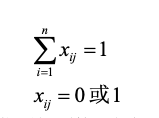
更复杂的问题：用✔️标记未选中的0的行，然后对该0所在列选中的0行标记✔️, 然后对该行其他0所在列标记✔️,然后对✔️标记的行重复之前操作，直到✔️号标记的补行和✔️号标记的列覆盖所有的0元素为止。未覆盖的元素最小值m,对应标记行减去m,对应标记列加上m可以得到新的等价变换矩阵，得到最优指派问题的解。

 

 多目标规划模型：

       

模型一：固定风险上限，最大化收益；

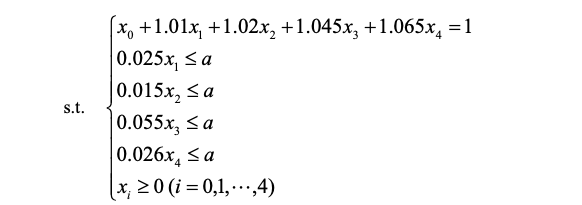
x0表示存银行，但收益率很低只有5%，

因为不同人可接受的风险度的上限不同，所以对a从0到0.05进行遍历，步长为0.001。 对于每一个a，得到当前a情况下最优的收益Q，做出Q-a图像。

代码如下：

clc,clear

a=0;

hold on

while a<0.05

c=[-0.05,-0.27,-0.19,-0.185,-0.185];

A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])]; 

b=a*ones(4,1);

Aeq=[1,1.01,1.02,1.045,1.065];

beq=1;

lb=zeros(5,1); 

[x,Q]=linprog(c,A,b,Aeq,beq,lb);

D = std(x);

Q=-Q;

plot(a,Q,'*b');

plot(a,D,'^r');

a=a+0.001;

end

xlabel('a'),ylabel('Q')

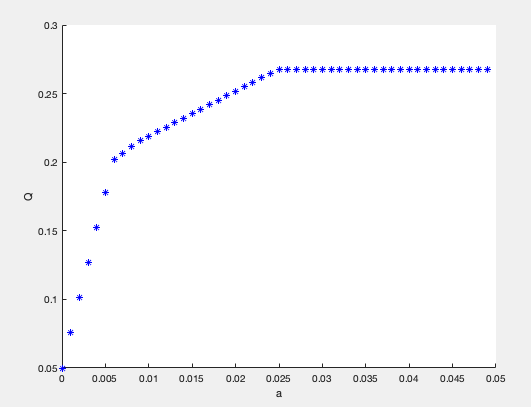
由图像可以看出当a取0.025附近时候，最优Q已经达到了最大值，之后不再改变，a只会影响Q的下限，而不会影响Q的上限。

红色点表示解的方差值，可见投资较为分散时，投资者承担的风险越小，与题意一致（a<0.5%时）。

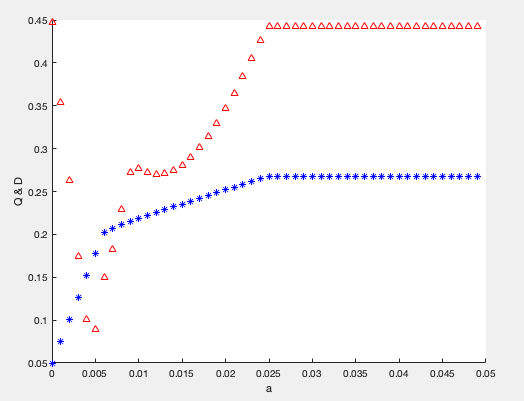
可见在0.006处左边Q增长很快，右边增长很慢，所以a = 0.006时候的Q值为相对最优解，

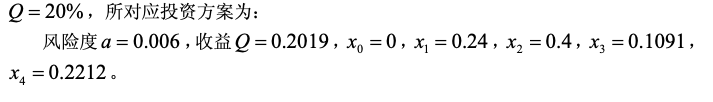
模型二：

 

代码如下：

clc,clear
k=0;
hold on
while k<0.25
c=[zeros(1,5),1]';
a1=[-0.05,-0.27,-0.19,-0.185,-0.185,0];
a2=[diag([0,0.025,0.015,0.055,0.026]),-1*ones(5,1)];
A=[a1;a2];
b=[-k,zeros(1,5)]';
Aeq=[1,1.01,1.02,1.045,1.065,0];
beq=1;
lb=zeros(6,1); 
[x,minrisk]=linprog(c,A,b,Aeq,beq,lb);
Q = -a1*x;
plot(k,minrisk*10,'*b'); 
plot(k,Q,'^r');
k=k+0.005;
end
xlabel('k'),ylabel('Q & 10*minrisk')

输出：

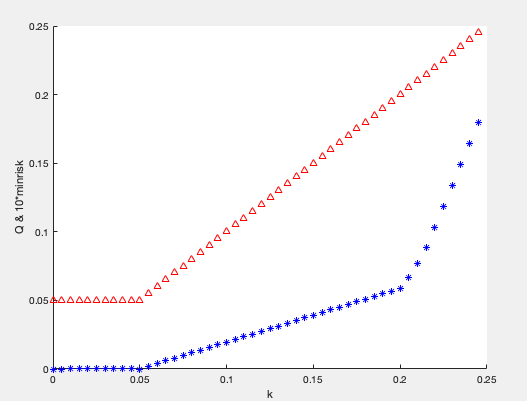
可见随着自己设置的最低收益率k的增加，Q值先不变（保持0.005，为全储存银行所得收益率），然后增加；

minrisk最小风险也随着k增加而增加，在k小于0.2时候，风险增加缓慢，大于0.2时候，风险增加速度突然加快，所以

k = 0.20时候的Q值为最优解，保证了风险较小并且收益率较大。

此时Q = 20% ，解同模型一；

模型三：

clc,clear
s=0;
hold on
while s<1
c=(1-s)*[-0.05,-0.27,-0.19,-0.185,-0.185,0]'+s*[zeros(1,5),1]';
a1=[-0.05,-0.27,-0.19,-0.185,-0.185,0];
A=[diag([0,0.025,0.015,0.055,0.026]),-1*ones(5,1)];
b=zeros(5,1);
Aeq=[1,1.01,1.02,1.045,1.065,0];
beq=1;
lb=zeros(6,1); 
[x,fval]=linprog(c,A,b,Aeq,beq,lb);
Q = -a1*x;
plot(s,fval,'*b'); 
plot(s, Q,'^r');
s=s+0.02;
end
xlabel('s'),ylabel('Q & fval')

输出：

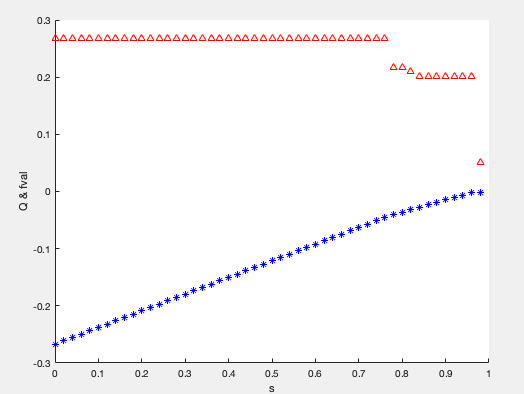
可见随着风险的加权系数越来越高，使得最大收益率呈梯度下降，当s = 0.764时候Q开始呈断崖式下降，之后收益率一直比较小，

该点s = 0.764, 可见我们此刻更看重的是风险，但同时也侧重收益率，所以此时的Q最优。

Q 接近20%，与上面的模型所得结论基本一致。