题意:给一个三脚阵,第i行有i个点。皇后可以攻击三脚阵中六方向上的所有点,给定三脚阵的边长n,已知最多可以放floor((n * 2 + 1) / 3)个互不冲突的皇后,要求给出一种方案。
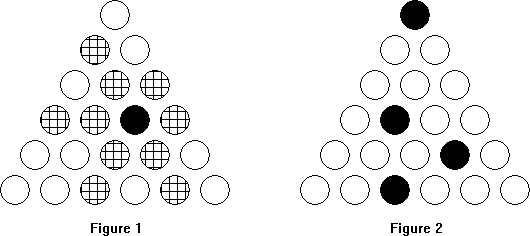
分析:根据题中数据找规律,进行构造,n<3的是特殊情况,每个点坐标用两个值表示,[i,j]表示第i行的第j个点,我们发现把这(n * 2 + 1) / 3个放皇后的坐标,从右往左看,发现i是从n开始每次递减1。从左往右看j的变化规律是1,3,5,7……2,4,6,8……,先奇数从1递增,然后偶数从2递增,那么分界线在哪呢?就是i>=j的时候是奇数,i增长慢但起点高,j增长快但起点底,j必然在某一点超越i,在超越之前j是奇数,超越之后j是偶数。
 View Code
View Code
#include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> using namespace std; int main() { //freopen("t.txt", "r", stdin); int t; scanf("%d", &t); for (int i = 0; i < t; i++) { int n; int cnt = 0; scanf("%d", &n); if (n < 3) { printf("%d %d 1\n[1,1]\n\n", i + 1, n); continue; } printf("%d %d %d\n", i + 1, n, (2 * n + 1) / 3); int a = n - (2 * n + 1) / 3 + 1; int b = 1; while (b <= a) { printf("[%d,%d] ", a, b); cnt++; if (cnt % 8 == 0) puts(""); b += 2; a++; } b = 2; while (a <= n) { printf("[%d,%d] ", a, b); cnt++; if (cnt % 8 == 0) puts(""); b += 2; a++; } if (cnt % 8) puts(""); puts(""); } return 0; }
