题意:给出图中所有线段,和一个点,问这个点要出正方形至少穿越多少线。
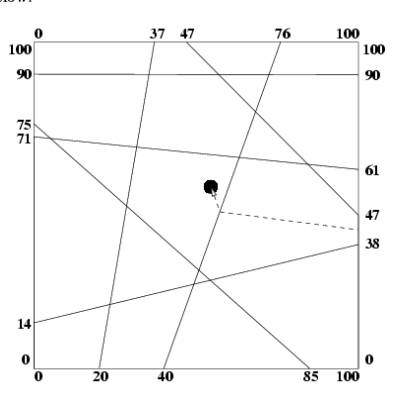
分析:所有线段端点都在正方形周边线上。走弯路是无意义的,不会使穿过的墙减少,因为线段都是接边界的,无法绕过。我们枚举周边线上的出口,连直线,看最少有几个交点。因为只有跨越端点的时候才会改变交点数量。所以我们只需在每两个端点间枚举一个点。
 View Code
View Code
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
#define maxn 50
#define zero(x) (((x)>0?(x):-(x))<eps)
#define eps 1.0E-8
struct Point
{
double x, y;
Point()
{
}
Point(double xx, double yy) :
x(xx), y(yy)
{
}
} point[maxn * 2], s;
struct Line
{
Point a, b;
Line()
{
}
Line(Point aa, Point bb) :
a(aa), b(bb)
{
}
} line[maxn];
int n, m, ans;
bool operator <(const Point &a, const Point &b)
{
return atan2(a.y, a.x) < atan2(b.y, b.x);
}
double xmult(Point p1, Point p2, Point p0)
{
return (p1.x - p0.x) * (p2.y - p0.y) - (p2.x - p0.x) * (p1.y - p0.y);
}
int same_side(Point p1, Point p2, Line l)
{
return xmult(l.a, p1, l.b) * xmult(l.a, p2, l.b) > eps;
}
int dots_inline(Point p1, Line l)
{
return zero(xmult(p1, l.a, l.b));
}
int dot_online_in(Point p, Line l)
{
return zero(xmult(p, l.a, l.b)) && (l.a.x - p.x) * (l.b.x - p.x) < eps && (l.a.y - p.y) * (l.b.y - p.y) < eps;
}
int intersect_in(Line u, Line v)
{
if (!dots_inline(v.a, u) || !dots_inline(v.b, u))
return !same_side(u.a, u.b, v) && !same_side(v.a, v.b, u);
return dot_online_in(u.a, v) || dot_online_in(u.b, v) || dot_online_in(v.a, u) || dot_online_in(v.b, u);
}
int opposite_side(Point p1, Point p2, Line l)
{
return xmult(l.a, p1, l.b) * xmult(l.a, p2, l.b) < -eps;
}
int intersect_ex(Line u, Line v)
{
return opposite_side(u.a, u.b, v) && opposite_side(v.a, v.b, u);
}
void input()
{
scanf("%d", &m);
n = 0;
for (int i = 0; i < m; i++)
{
scanf("%lf%lf", &point[n].x, &point[n].y);
point[n].x -= 50;
point[n].y -= 50;
n++;
scanf("%lf%lf", &point[n].x, &point[n].y);
point[n].x -= 50;
point[n].y -= 50;
n++;
line[i] = Line(point[i * 2], point[i * 2 + 1]);
}
point[n].x = -50;
point[n++].y = -50;
point[n].x = 50;
point[n++].y = 50;
point[n].x = 50;
point[n++].y = -50;
point[n].x = -50;
point[n++].y = 50;
scanf("%lf%lf", &s.x, &s.y);
s.x -= 50;
s.y -= 50;
}
Point mid_point(Point &a, Point &b)
{
return Point((a.x + b.x) / 2, (a.y + b.y) / 2);
}
void work()
{
point[n] = point[0];
ans = m;
for (int i = 0; i < n; i++)
{
Line l(s, mid_point(point[i], point[i + 1]));
int temp = 0;
for (int i = 0; i < m; i++)
if (intersect_in(l, line[i]))
temp++;
ans = min(ans, temp);
}
}
int main()
{
//freopen("t.txt", "r", stdin);
input();
sort(point, point + n);
// for (int i = 0; i < n; i++)
// printf("%f %f\n", point[i].x, point[i].y);
work();
printf("Number of doors = %d\n", ans + 1);
return 0;
}
