圆方树的定义
圆方树是由一个无向图转化出的树形结构。转化方法为:
- 所有原图的点为“圆点”。
- 对于每个点双连通分量:
- 删去点双内部“圆点”间的连边。
- 新建点双的代表点——“方点”。
- 方点向点双内的所有点连边。
举个例子:
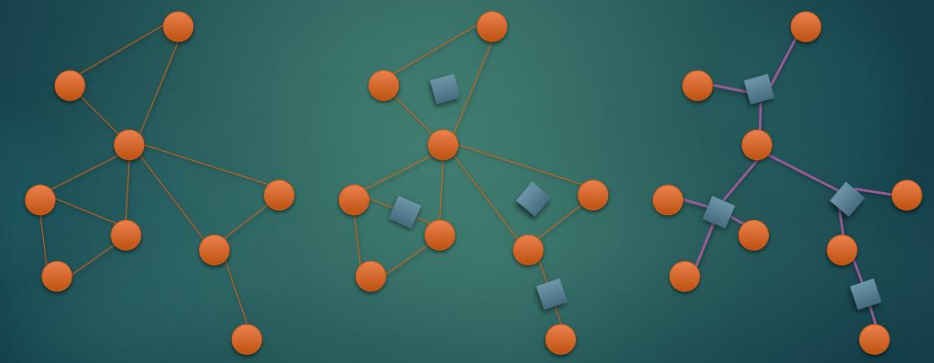
观察图片,我们可以得到圆方树的一些性质:
- 不存在相邻的方点。
- 一个圆点同时隶属于它所邻接的所有方点所代表的点双。可见所有非叶子圆点都是原图的割点。
- 从圆点 \(u\) 到圆点 \(v\) 的树上路径所经过的圆点是原图 \(u\) 到 \(v\) 的所有路径一定经过的点。
圆方树的构造
既然跟点双相关,那肯定是 \(\text{Tarjan}\) 老爷爷上场啦!
圆方树的构造算法实质上就是在求点双的基础上构建一个新图。设当前结点为 \(u\),若发现其儿子(DFS 树上儿子)\(v\) 的 low[v]>=dfn[u],那么就知道 \(u\) 是一个割点或者是 DFS 树根。我们不必对此加以区分,直接将 \(u\) 和新建的方点 \(w\) 连边,然后 \(w\) 向所有退栈的点连边,圆方树就构造完成了。
实现
inline void Tarjan ( const int u, const int f ) {
dfn[u] = low[u] = ++ dfc, stk[++ tp] = u;
adj ( src, u, v ) if ( v ^ f ) { // 枚举原图上u的临界点,并保证其不是DFS树上u的父亲。
if ( ! dfn[v] ) {
Tarjan ( v, u ), chkmin ( low[u], low[v] );
if ( low[v] >= dfn[u] ) {
tre.add ( u, ++ snode ); // snode初值为n,用于计数新建结点。
do tre.add ( snode, stk[tp] ); while ( stk[tp --] ^ v );
// 向每个退栈的点连边。
}
} else chkmin ( low[u], dfn[v] );
}
}
细节
在运用圆方树的过程中,我们往往需要在方点维护一些信息。为了避免重复,我们一般在割点处单独维护圆点信息,而在方点中不考虑割点。(即在上文算法中,结点 \(snode\) 不考虑 \(u\) 的信息,只记录 \(v\) 的信息。)
圆方树的运用
「BZOJ 3331」压力
\(\mathcal{Description}\)
Link.
给定一个 \(n\) 个点 \(m\) 条边的连通无向图,并给出 \(q\) 个点对 \((u,v)\),令 \(u\) 到 \(v\) 的路径所必经的结点权值 \(+1\)。求最终每个结点的权值。
\(n\le10^5\),\(m,q\le2\times10^5\)。
\(\mathcal{Solution}\)
看到”必经之点“,应该考虑圆方树。
对于每个点对,直接在圆方树上作差分,最后一遍 DFS 求每个圆点的子树和即可。
详细题解:my solution。
「洛谷 P4320」道路相遇
\(\mathcal{Description}\)
Link.
给定一个 \(n\) 个点 \(m\) 条边的连通无向图,并给出 \(q\) 个点对 \((u,v)\),询问 \(u\) 到 \(v\) 的路径所必经的结点个数。
\(n,q\le5\times10^5\),\(q\le\min\{\frac{n(n-1)}2,10^6\}\)。
\(\mathcal{Solution}\)
和上一道几乎一样。预处理圆方树上每个点到根经过的圆点个数,然后求 LCA 计算答案。
详细题解:my solution。
「APIO 2018」「洛谷 P4630」铁人两项
\(\mathcal{Description}\)
Link.
给定一个 \(n\) 个点 \(m\) 条边的无向图(不保证联通),求有序三元点对 \((s,c,f)\) 的个数,满足 \(s,c,f\) 互不相同,且存在一条从 \(s\) 到 \(c\) 再到 \(f\) 的简单路径。
\(n\le10^5\),\(m\le2\times10^5\)。
\(\mathcal{Solution}\)
首先考虑这样一个问题,若 \(s,c,f\) 在同一点双中,是否一定满足条件。
答案是肯定的,这里不细说。
那么如果固定 \(s,f\),合法的 \(c\) 就可以在圆方树 \(s\) 到 \(f\) 路径上的所有圆点和所有方点所代表的圆点(除去 \(s,f\))。这是因为 \(c\) 取在任意点双内部,由我们的结论,都一定可以从某点进入点双,经过 \(c\),再从某点走出点双。
但简单的计算会导致重复——一个圆点对多个方点有贡献。
举个例子,对于 \(u-w-v\),\(w\) 是圆点,\(u,v\) 是方点,如果我们单纯地用点双大小作为方点的权值,\(w\) 就会在 \(u\) 和 \(v\) 中分别计算一次。
解决办法很巧妙:将圆点的权值设为 \(-1\)。考虑 \(s\) 到 \(f\) 的路径必然是”圆-方-圆-……-圆-方-圆“,两个端点的 \(-1\),去除了 \(s\) 和 \(f\) 的贡献,中间的 \(-1\) 去除了在左右的”方“中重复的贡献。那么,合法的 \(c\) 的数量就是 \(s\) 到 \(f\) 的树上路径权值之和。
于是,相当于求树上点对的路径权值和。反过来,固定 \(c\),维护子树信息求出 \((s,f)\) 的方案数,计算 \(c\) 的贡献即可。
详细题解:my solution(带上文所述性质的证明)。
「CF 487E」Tourists
\(\mathcal{Description}\)
Link.
维护一个 \(n\) 个点 \(m\) 条边的简单无向连通图,点有点权。\(q\) 次操作:
- 修改单点点权。
- 询问两点所有可能路径上点权的最小值。
\(n,m,q\le10^5\)。
\(\mathcal{Solution}\)
怎么可能维护图嘛,肯定是维护圆方树咯!
一个比较 naive 的想法是,每个方点维护其邻接圆点的最小值,树链剖分处理询问。
不过修改的复杂度会由于菊花退化:修改”花蕊“的圆点,四周 \(\mathcal O(n)\) 个方点的信息都需要修改。
联想到 array 这道题,我们尝试”弱化“方点所维护的信息。每个方点,维护其圆方树上儿子们的点权最小值。那么每次修改圆点,至多就只有其父亲需要修改信息了。
于是,每个方点用 std::multiset 或者常见的双堆 trick 维护最小值信息(推荐后者,常数较小),再用一样的树剖处理询问即可。
详细题解:my solution。
「SDOI 2018」「洛谷 P4606」战略游戏
\(\mathcal{Description}\)
Link.
给定一个 \(n\) 个点 \(m\) 条边的无向连通图,\(q\) 次询问,每次给出一个点集 \(s\),求至少在原图中删去多少个点,使得 \(s\) 中存在两点不连通。多组数据。
每组数据 \(n,q\le10^5\),\(m,\sum|s|\le2\times10^5\)。
\(\mathcal{Solution}\)
看到 \(\sum|s|\) 的限制,不难联想到虚树或者其它与 DFN 相关的算法。
所以,先建出圆方树,并处理好 DFN,LCA 的一系列信息。考虑到答案就是 \(s\) 中的点在树上构成的连通块中不在 \(s\) 集合里的圆点个数,可以求一个树上前缀和:\(sum_u\) 表示从 \(u\) 到根路径上的圆点个数。处理询问时,先将 \(s\) 按 DFN 从小到大排序,两两 LCA 计算贡献(\(s_1\) 和 \(s_{|s|}\) 也要算一次),最后除以 \(2\),得到 \(cnt\)。不过整个连通块的根(\(\operatorname{LCA}(s_1,s_{|s|})\))这个点的贡献被遗漏了,所以要再加上这个点单独的贡献。最终答案就是 \(cnt-|s|\)。
详细题解:my solution。
「BZOJ 4316」小C的独立集
\(\mathcal{Description}\)
Link.
求包含 \(n\) 个结点 \(m\) 条边的仙人掌的最大独立集。
\(n\le5\times10^4\),\(m\le6\times10^4\)。
\(\mathcal{Solution}\)
建出圆方树,考虑树上 DP。
设状态 \(f(i,0/1)\) 表示该点不选择/不限制选择与父亲相邻的圆点(对于圆点,即它本身)时,子树内的最大独立集。转移分圆点和方点讨论:
-
圆点:很显然,\(f(u,0)=\sum_{v\in son_u}f(v,1),f(u,1)=\max\{f(u,0),\sum_{v\in son_u}f(v,0)+1\}\)。
-
方点:考虑把环展开成链。在链上做一个子 DP,这里不赘述。
最后,\(f(root,1)\) 就是答案。
详细题解:my solution(含子 DP 详细说明)。
「洛谷 P5236」「模板」静态仙人掌
\(\mathcal{Description}\)
Link.
给定一个 \(n\) 个点 \(m\) 条边的仙人掌,\(q\) 组询问两点最短路。
\(n,q\le10^4\),\(m\le2\times10^4\)。
\(\mathcal{Solution}\)
提出一个环来考虑,从环上一点 \(u\) 到 \(v\),无非两条路径。可以按顺序处理一个前缀和,计算两条路径边权的最小值。这里不细说。
建圆方树(很多题解说建树的细节与普通图不一样,其实正常建也没有任何问题 qwq),发现一个圆点走进方点(点双),在走到父亲圆点的最短距离可以在 \(\text{Tarjan}\) 算法中预处理出来。考虑圆方树上的边权:圆点到父亲方点的边权为上述最短距离,否则为 \(0\)。对于询问 \((u,v)\),找到其 \(\text{LCA}\)(设为 \(w\)),分 \(w\) 的情况讨论:
- \(w\) 是圆点,那么 \(\text{LCA}\) 时求出的树上距离就是答案。
- \(w\) 是方点,此时树上距离实际上是 \(u\) 和 \(v\) 走到 \(w\) 的父亲圆点的距离之和,明显时错误的——\(u\) 和 \(v\) 走进同一个点双后,需要求一次最短距离而非直接在父亲会和。所以可以倍增求到 \(u\) 走进点双的第一个点(即方点向 \(u\) 点方向的儿子圆点)\(u'\),同理求出 \(v'\),利用处理的前缀和求到 \(u'\) 到 \(v'\) 的最短距离。那么答案就是 \(\operatorname{dist}(u,u')+\operatorname{dist}(u',v')+\operatorname{dist}(v',v)\)。
详细题解:my solution(含带图的环上前缀和讲解)。
「HNOI 2009」「洛谷 P4410」无归岛
\(\mathcal{Description}\)
Link.
原题的题目描述愣是没看懂 qwq。
给一个 \(n\) 个点 \(m\) 条边的仙人掌(或许有特殊性质,不过这里的解法不需要 www),点有点权,求带权最大独立集。
\(n\le10^5\),\(m\le2\times10^5\)。
\(\mathcal{Solution}\)
和上上题几乎一样,把圆点的 \(+1\) 改成 \(+\max\{0,a_u\}\) 就好。
我绝对不会告诉你我快读没判负数挂了三次 qwq。
详细题解:看上上题的吧,再水一篇太过分了 www。