Java 位运算总结

一、Java中支持的位运算

1. 位与（&）：二元运算符，两个为1时结果为1，否则为0
2. 位或（|）：二元运算符，两个其中有一个为1时结果就为1，否则为0
3. 位异或（^）：二元运算符，两个数同时为1或0时结果为1，否则为0
4. 位取非（~）：一元运算符，取反操作
5. 左移（<<）：一元运算符，按位左移一定的位置。高位溢出，低位补符号位，符号位不变。
6. 右移（>>）：一元运算符，按位右移一定的位置。高位补符号位，符号位不变，低位溢出。
7. 无符号右移（>>>）：一元运算符，符号位（即最高位）保留，其它位置向右移动，高位补零，低位溢出。

二、位运算规则

　　Java数值运算过程中都是先将十进制转换为二进制然后再进行运算，再把二进制数据转换为十进制展现给用户。二进制运算规则如下：

　　对于有符号的而言，

• 最高位为符号位，0表示正数，1表示负数
• 正数的原码，反码和补码都一样，三码合一
• 负数的反码：符号位保持不限，其他位取反
• 负数的补码：补码 + 1
• 0的反码和补码都是0
• 计算机的运算的时候，都是将原码转成补码进行运算的

　　下面以 -1 为例子展示原码、反码和补码的转换关系（以int数据类型为例，int类型在Java中占4字节）：

　　

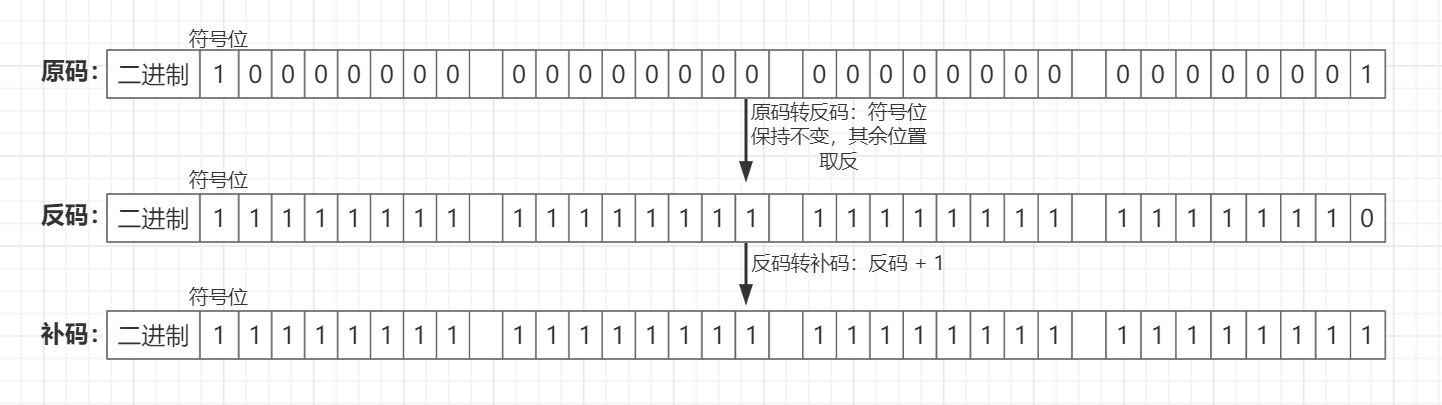
三、逻辑运算

（一）、与运算（&）

　　一、运算规则

　　　　两个数相同位置的比特进行与运算，若两个位置均为1，那么结果就为1，否者为0。

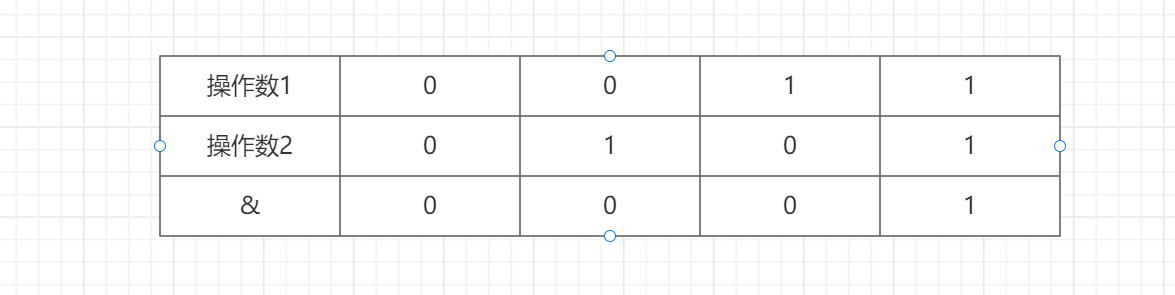
　　二、运算流程

　　以 4 & -5 = 0为例子展示运算流程：

　　1. 因为4为正数，所以原码和补码相同，即4的补码为：00000000 0000000 00000000 00000100

　　2.因为-5为负数，所以需要进行原码 >>> 反码 >>> 补码的转换

　　　　1）原码：10000000 00000000 00000000 00000101

　　　　2）反码：11111111 11111111 11111111 11111010

　　　　3）补码：11111111 11111111 11111111 11111011

　　3.将4和-5的补码进行 & 运算：00000000 0000000 00000000 00000100

　　　　　　　　　　　　　　　   11111111 11111111 11111111 11111011         &

　　　　　　　　　　　　　　　00000000 00000000 00000000 00000000

　　4.得到的补码结果为：00000000 00000000 00000000 00000000。所以结果为0

（二）、或运算（|）

　　一、运算规则

　　　　两个数相同位置的比特进行或运算，若其中一个为1则结果为1，否个结果为0。

　　二、运算流程

　　以 -2 | 5 = -1为例展示运算流程：

　　1.-2为负数，需要进行原码 > 反码 > 补码的转换。转换步骤如下：　

　　　　1）原码：10000000 00000000 00000000 00000010

　　　　2）符号位不变，其他位置取反得反码：11111111 11111111 11111111 11111101

　　　　3）在反码的基础上＋1得到补码： 11111111 11111111 11111111 11111110

　　2.5为正数，补码和反码一致，所以5的补码为：00000000 00000000 00000000 00000101

　　3.将-2 和 5 的补码进行或运算： 11111111 11111111 11111111 11111110

　　　　　　　　　　　　　　　|    00000000 00000000 00000000 00000101 

　　　　　　　　　　　　　　　　  11111111 11111111 11111111 11111111

　　4.根据上面的运算得到补码结果为：11111111 11111111 11111111 11111111

　　5.结果显然是一个负数，而负数的补码和原码不一致，所以需要将补码结果转换为原码才能得到最终的结果

　　6.补码转原码的过程是跟原码转补码相反的过程，具体过程如下：

　　　　1）补码：11111111 11111111 11111111 11111111

　　　　2）补码 -1 得到反码：11111111 11111111 11111111 11111110

　　　　3）符号位不变，其他位置取反得：10000000 00000000 00000000 00000001

　　7.最终得到的原码结果为 10000000 00000000 00000000 00000001，转成十进制为 -1

（三）、异或运算（^）

　　一、运算规则

　　　　两个数相同位置的比特进行或运算，若两个数均为0或1，则结果为0，否者为1.

 

 　　二、运算流程

　　　　以 1 ^ -5 = 6 为例，具体运算流程如下：

　　　　1.1的补码为：00000000 00000000 00000000 00000001

　　　　2.-5的补码为：11111111 11111111 11111111 11111011（可参考与运算给出的流程）

　　　　3.两个补码运算：　　

　　　　　　　　　　00000000 00000000 00000000 00000001

　　　　　　　　^     11111111   11111111   11111111    11111011

　　　　　　　　　   11111111   11111111  11111111     11111010

　　　　4.得到的补码结果为：11111111   11111111  11111111     11111010

　　　　5.补码为负数，需要转换成原码：

　　　　　　1）补码：11111111   11111111  11111111     11111010

　　　　　　2）反码：11111111   11111111  11111111     11111001

　　　　　　3）原码：10000000 00000000 00000000 000000110

　　　　6.由原码：10000000 00000000 00000000 000000110，得出最终的时间结果为 -6.

（四）、取反运算（~）

　　一、运算规则

　　　　若位数为0，则取反后为1，若为1，取反后为0。

　　二、运算规则

　　　　以~2 = -3为例运算流程如下：

　　　　1.2的原码为：00000000 00000000 00000000 00000010

　　　　2.2的补码跟原码一致也为：00000000 00000000 00000000 00000010

　　　　3.取反：111111111 11111111 11111111 11111101

　　　　4.取反后的结果仍未补码，此时补码为负数，则需要转成原码

　　　　5. 11111111 11111111 11111111 11111101 - 1 得到反码：11111111 11111111 11111111 11111100

　　　　6. 11111111 11111111 11111111 11111100 符号位不变，其他位置取反得到原码为：10000000 00000000 00000000 00000011

　　　　7.  10000000 00000000 00000000 00000011 转成十进制结果为 -3

　　　　　　　　　　

四、位移操作

　　（一）、左移（<<）

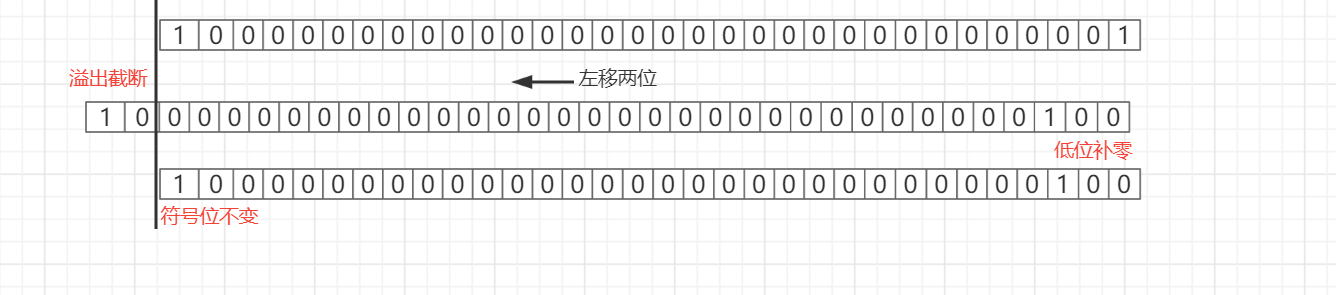
　　　　规则：符号位不变，高位溢出截断，低位补零。比如 -1 << 2 = -4 (为方便讲解，图示的补码为-1)

　　（二）、右移（>>）

　　　　规则：符号位不变，低位溢出截断，高位用符号位填充。如：8 >> 2 = 2。

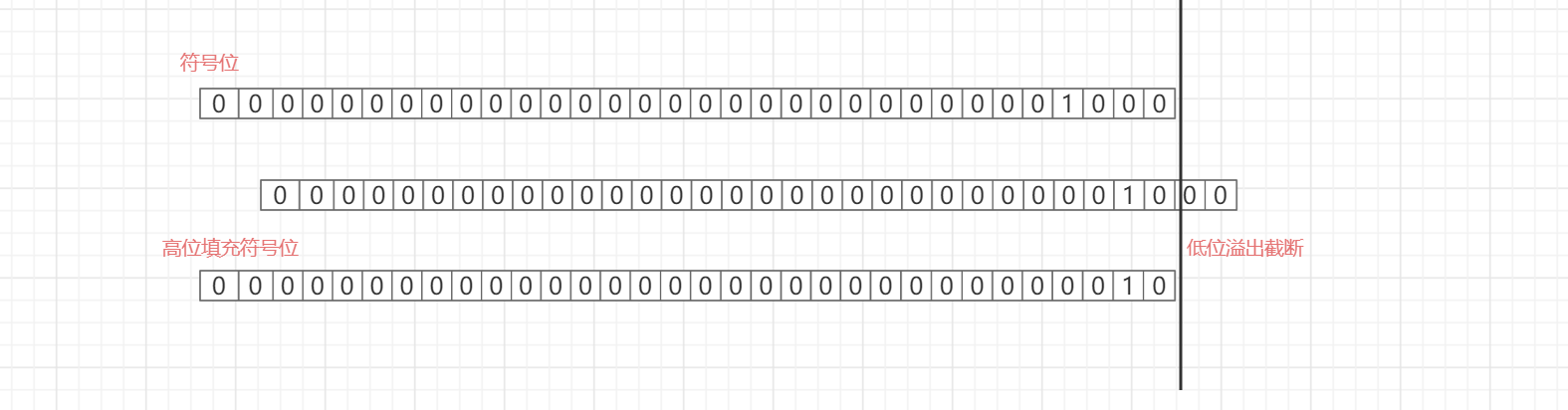
　　（三）、无符号右移（>>>）

　　　　规则：高位填充0，低位溢出。如-1>>>1=2147483647