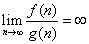Θ记号 Θ(g(n)) = { f(n) : 若存在正常数c1,c2和n0,使对所有n>=n0时有0<=c1*g(n)<=f(n)<=c2*g(n)} 确界
Ο记号 Ο(g(n)) = { f(n) : 存在正常数c和n0,使对所有n>=n0,有0<=f(n)<=c*g(n) } 渐进上界
Ω记号 Ω(g(n)) = { f(n) : 存在正常数c和n0,使所有n>=n0有0<=c*g(n)<=f(n) } 渐进下界
ο记号:非渐进上界 f(n) = o(g(n)) 意味着 
ω记号:非渐进上界 f(n) = o(g(n)) 意味着