红黑树

下面网址中是红黑树很好的教材，很详细。

http://blog.csdn.net/eric491179912/article/details/6179908

另外经典教材就是算法导论中关于红黑树的章节了，以算法导论为主，实在不明白的地方再去网上查找资料。

红黑树是一种特殊的二叉查找树，大家都知道二叉查找树的复杂度最坏情况为O(h)，为了减低最坏情况的复杂度，大神们设计了许多种二叉查找树的改进版本，红黑树便是其中之一，它可以保证在最坏情况下复杂度为O(lgn)，也就是说h < lgn。

红黑树的五个性质

1）每个节点或者是红色，或者是黑色

2）根节点是黑色

3）每个叶子节点是黑色的(此处的叶子节点指的是外部节点)

4）红色节点的两个孩子都是黑色的

5）对于每个节点，从该节点到其子孙叶子节点的所有路径上包含相同数目的黑色节点

红黑树节点的定义

typedef struct node
{
	int color;
	int key;
	struct node *p;//指向父节点
	struct node *left, *right;

}RBtreeNode;

与二叉搜索树相比较，多出了2部分，本节点的颜色属性和指向父节点是指针，之所以需要指向父节点是为了后序操作的便利。

红黑树的左旋和右旋

在节点x上左旋，是以x和x的右孩子y之间的轴为支点，旋转结束后x成为y的左孩子；在节点y上右旋，是以y和y的左孩子x之间的轴为支点，旋转结束后y是x的右孩子；如图所示

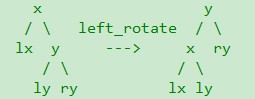
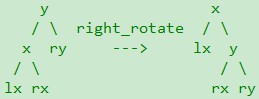   ，理论上与二叉搜索树的旋转没有任何区别

红黑树的插入

假设新插入节点z，我们将其置为红色，可能破坏性质2）和性质4），违反性质2）是因为新插入的点成为了根节点，违反性质4）是因为z->p也是红色；插入z后，从底向上逐层调整树的结构和颜色，使其仍然满足红黑树的性质。既然从底层开始调整，我们可以只考虑违反性质4），当然在调整过程中绝不允许出现违反其他性质的现象。

前提z的父亲是红色

case1--z的叔叔是红色

z的叔叔uncle_z是红色，那z的爷爷肯定是黑色，可以把z的父亲和叔叔置为黑色，z的爷爷置为红色，z <- z的爷爷，然后继续向上操作。

case2--uncle_z是黑色，且z和uncle_z不是同一方向的孩子，即z是左孩子，uncle_z是右孩子；或者z是右孩子，uncle_z是左孩子

　　case2.1--z是左孩子，uncle_z是右孩子，如下面左图所示。我们以z的爷爷为输入，做一次右旋操作，同时把parent_z置为黑色，gparent_z置为红色，整棵树调整结束。

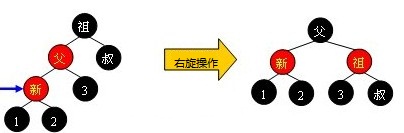     左右分割   

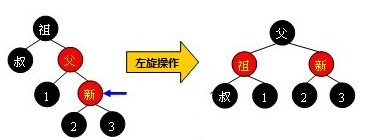
　　case2.2--z是右孩子，uncle_z是左孩子，如上面右图所示。我们，以z的爷爷为输入，做一次左旋操作，同时把parent_z置为黑色，gparent_z置为红色，整棵树调整结束。

 可以看到，case2.1和case2.2是对称的两种情况。

case3--uncle_z是黑色，且z和uncle_z是同一方向的孩子，即z是左孩子，uncle_z也是左孩子；或者z是右孩子，uncle_z也是右孩子

 　　case3.1--z和uncle_z同时是左孩子，如下面左图所示。我们以z的父亲为输入，做一次右旋操作，同时把z置为旋转前z的父亲，变成了case2.2，有木有！！

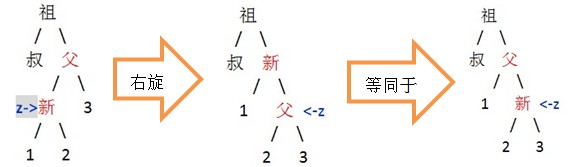  左右分割  

　　case3.2--z和uncle_z同时是右孩子，如上面右图所示。我们以z的父亲为输入，做一次左旋操作，同时把z置为旋转前z的父亲，变成了case2.1。

插入的最后，在把root的颜色置为黑色，完事。

 红黑树的删除

假设被删除节点是z，可以找到真正要被删除的节点y，即如果z至多有一个孩子，y等于z；否则y是z的中序后继，此时y至多有一个右孩子；总的说来y至多只有一个右孩子x。如果y是红色，删除y后仍然能够保证红黑树的5个性质；如果y是黑色，可能违反性质2），4），5）。删除y时就是把x代替了y的位置，我们可以给x额外增加一个黑色，使其成为了双黑色和红黑色，这样满足了性质5），但违反性质1）。

如果x是红黑色，我们将其置为黑色，调整结束；

如果x是根节点，我们将其置为黑色，结束；

如果x是双黑色，做必要的旋转和涂色。

假设parent_x为删除节点y后x的父节点，实际上就是y的父节点，那么parent_x一定是有两个孩子的，因为此时y非空，且y是黑色，在不违反性质5）的前提下，y一定有兄弟。令parent_x的另一个孩子为w，即x的兄弟为w

case1--w为黑色，且w的两个孩子都是黑色

因为w是黑色，x是双重黑色，可以同时去掉x和w的黑色，x的父节点增加一重黑色，不会违反性质5），然后把x赋值给x的父节点，继续循环。如下面两幅图所示

    左右分割  

 case2--w是黑色，且w同一方向的孩子是红色，即若w是左孩子，w的左孩子是红色；若w是右孩子，w的右孩子是红色。我们可以通过旋转使x的高度减一，并且在x和x的父亲之间增加一个黑色节点，最后把x置为根节点，循环结束

　　case2.1--w是黑色，w是左孩子，w的左孩子是红色，以w的父节点为输入，做一次左旋，并且做一些颜色涂改

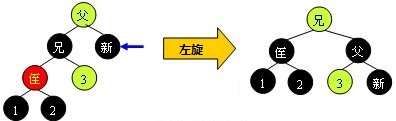   左右分割   

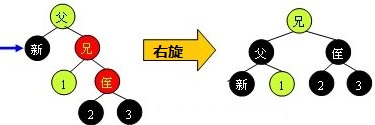
 　　case2.2--w是黑色，w是右孩子，w的右孩子是红色，以w的父节点为输入，做一次右旋，并且做一些颜色涂改

 case3--w是黑色，w同一方向的孩子是黑色，我们可以通过旋转使其转化为case2

　　case3.1--w是黑色，w是左孩子，w的左孩子是黑色，那么右孩子一定是红色，否则就成了case1;以w为输入，做一次右旋，变成了case2.1

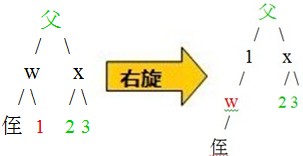    左右分割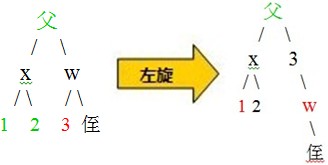  

　　case3.2--w是黑色，w是右孩子，w的右孩子是黑色，那么左孩子一定是红色，否则就成了case1;以w为输入，做一次左旋，变成了case2.2

  case4--w是红色的，则w肯定有黑孩子，parent_x是黑色的，以parent_x为输入，做一次左旋，可转变成case1,case2,或者case3

 

 附源代码，另附测试数据的大神博客网址：http://blog.csdn.net/v_JULY_v/article/details/6284050

//红黑树基本操作
#include <stdio.h>
#include <list>

#define BLACK 0
#define RED 1
typedef struct node
{
	int color;
	int key;
	struct node *p;
	struct node *left, *right;

}treeNode;

//在节点x上左旋操作，以x和x右孩子之间的轴为支点，旋转结束后x成为y的左孩子
//      x                  y
//     /    left_rotate  /  
//    lx  y     --->     x  ry
//       /             / 
//      ly ry          lx ly
treeNode* left_rotate(treeNode* root, treeNode* x)
{
	treeNode *y = x->right;
	x->right = y->left;
	if(y->left != NULL)
		(y->left)->p = x;
	y->p = x->p;
	if(x->p == NULL)//x是根节点
		root = y;
	else if(x == (x->p)->left)
		(x->p)->left = y;
	else (x->p)->right = y;
	y->left = x;
	x->p = y;

	return root;
}

//在节点y上的右旋操作，以y和y的左孩子x之间的轴为支点，旋转结束后y是x的右孩子
//      y                  x
//     /   right_rotate  /  
//    x  ry     --->     lx  y
//   /                     /           
//  lx rx                  rx ry
treeNode* right_rotate(treeNode* root, treeNode* y)
{
	treeNode *x = y->left;
	y->left = x->right;
	if(x->right != NULL)
		(x->right)->p = y;
	x->p = y->p;
	if(y->p == NULL)//y是根节点
		root = x;
	else if(y == (y->p)->left)
		(y->p)->left = x;
	else (y->p)->right = x;
	x->right = y;
	y->p = x;
	return root;
}

//插入新的节点后必须得调整
treeNode* rb_insert_fixup(treeNode *root, treeNode *z)
{
	treeNode *uncle_z;
	while(z->p && z->p->color == RED && z->p->p)
	{
		if (z->p->p->left == z->p)//z的父亲是左孩子
		{
			uncle_z = z->p->p->right;//z的叔父是右孩子
			//case1--叔父是右孩子，红色
			if(uncle_z && uncle_z->color == RED)
			{
				uncle_z->color = BLACK;
				z->p->color = BLACK;
				z->p->p->color = RED;
				z = z->p->p;
			}
			//case1 end
			else
			{	
				//case2--叔父是右孩子，黑色 z是右孩子
				if (z == z->p->right)//如果z是右孩子
				{
					z = z->p;
					root = left_rotate(root, z);
				}
				//case2 end 
				//case3--叔父是右孩子，黑色 z是左孩子
				z->p->color = BLACK;
				z->p->p->color = RED;
				root = right_rotate(root, z->p->p);
				//case3 end
			}
		}
		else//z的父亲是右孩子
		{
			uncle_z = z->p->p->left;//z的叔父是左孩子
			//case4--叔父是左孩子，红色
			if (uncle_z && uncle_z->color == RED)
			{
				uncle_z->color = BLACK;
				z->p->color = BLACK;
				z->p->p->color = RED;
				z = z->p->p;
			}
			//case4 end
			else 
			{	
				//case5--叔父是左孩子，黑色，z是左孩子
				if (z == z->p->left)
				{
					z = z->p;
					root = right_rotate(root, z);
				}
				//case5 end
				//case6--叔父是左孩子，黑色 z是右孩子
				z->p->color = BLACK;
				z->p->p->color = RED;
				root = left_rotate(root, z->p->p);
				//case6 end
			}
		}
	}
	root->color = BLACK;
	return root;
}

//插入新的节点
treeNode* rb_insert(treeNode *root, int value)
{
	treeNode *z = new treeNode;
	z->key = value;
	treeNode *x = root;
	treeNode *y = NULL;

	while(x != NULL)
	{
		y = x;
		if(value == x->key)
			return root;
		if(value < x->key)
			x = x->left;
		else x = x->right;
	}
	z->p = y;
	if (y == NULL)
	{
		root = z;
	}
	else
	{
		if(value < y->key)
			y->left = z;
		else
			y->right = z;
	}
	z->left = NULL;
	z->right = NULL;
	z->color = RED;
	root = rb_insert_fixup(root, z);
	return root;
}
//删除节点x的父节点后调整, x相当于多重黑色或者红黑色
treeNode* rb_delete_fixup(treeNode *root, treeNode *x, treeNode *parent_x)
{
	treeNode *w;//x_brother
	while(x!=root && (x == NULL ||x->color == BLACK))
	{
		//x的父亲parent_x一定有两个孩子
		if(x == parent_x->left)
		{
			w = parent_x->right;//x的右兄弟w
			//case1--x的兄弟w为红色，则w肯定有黑孩子,左旋,转换成case2,case3....
			if(w->color == RED)
			{
				w->color = BLACK;
				parent_x->color = RED;
				root = left_rotate(root, parent_x);
				w = parent_x->right; //w重新置为parent_x的右孩子
			}
			//case1 end
			//case2--w为黑色，w的两个孩子(如果有)也是黑色
			if((w->left == NULL || w->left->color == BLACK) && (w->right == NULL || w->right->color == BLACK))
			{
				w->color = RED;
				x = parent_x;
				parent_x = parent_x->p;
			}
			//case2 end	
			else
			{	//case3--w的右孩子是黑色，左孩子是红色
				if(w->right == NULL || w->right->color == BLACK)
				{
					if(w->left != NULL)//如果w有左孩子,一定是红色
						w->left->color = BLACK;
					w->color = RED;
					root = right_rotate(root, w);
					w = parent_x->right;
				}
				//case3 end
				//case4 w的右孩子是红色
				if (w->right != NULL)//如果w有右孩子，一定是红色
					w->right->color = BLACK;
				w->color = parent_x->color;
				parent_x->color = BLACK;	
				root = left_rotate(root, parent_x);
				x = root;
			}
		}
		else//与上面对称
		{
			w = parent_x->left;//x的左兄弟w
			//case5--x的兄弟w为红色，则w肯定有黑孩子,右旋,转换成case2,case3....
			if(w->color == RED)
			{
				w->color = BLACK;
				parent_x->color = RED;
				root = right_rotate(root, parent_x);
				w = parent_x->left;
			}
			//case5 end
			//case6--w为黑色，w的两个孩子(如果有)也是黑色
			if((w->left == NULL || w->left->color == BLACK) && (w->right == NULL || w->right->color == BLACK))
			{
				w->color = RED;
				x = parent_x;
				parent_x = parent_x->p;
			}
			//case6 end
			else
			{
			//case7--w的左孩子是黑色，右孩子是红色
				if(w->left == NULL || w->left->color == BLACK)
				{
					if(w->right != NULL)
						w->right->color = BLACK;
					w->color = RED;
					root = left_rotate(root, w);
					w = parent_x->left;
				}
				//case7 end
				//case8 w的左孩子是红色
				if (w->left->color == RED)
					w->left->color = BLACK;
				w->color = parent_x->color;
				parent_x->color = BLACK;	
				root = right_rotate(root, parent_x);
				x = root;
				//case8 end
			}
		}
	}

	if(x != NULL)
		x->color = BLACK;
	return root;
}

treeNode* rb_delete(treeNode *root, int value)
{
	treeNode *z, *y, *x;
	z = root;
	while(z != NULL)
	{
		if(z->key == value)
			break;
		if(z->key < value)
			z = z->right;
		else
			z = z->left;
	}
	if(z == NULL) //木有找到要删除的节点
		return root;
	y = z;
	if(y->left!=NULL && y->right!=NULL)//两个孩子的情况，y是z的中序后继
	{
		y = y->right;
		while (y->left != NULL)
		{
			y = y->left;
		}
		z->key = y->key;
	}
	//x是y唯一的孩子或者NULL
	if(y->left != NULL)
		x = y->left;
	else x = y->right;
	
	if(x)
		x->p = y->p;
	if(y->p == NULL)//y是根节点
		root = x;
	else if(y == y->p->left)
		y->p->left = x;
	else y->p->right = x;
	
	if(y->color==BLACK)
		root = rb_delete_fixup(root, x, y->p);
	delete y;
	return root;
}

treeNode* rb_find(treeNode *root, int value)
{
	treeNode *x = root;
	int h = 0;
	while (x != NULL)
	{
		if (x->key == value)
		{
			if(x->color == RED)
				printf("RED ");
			else
				printf("BLACK ");
			printf("从0层计数，%d在第%d层
", value, h);
			return x;
		}
		if (x->key < value)
			x = x->right;
		else x = x->left;
		h++;
	}
	return NULL;
}

void midOrder(treeNode *root)
{
	if(root == NULL)
		return;
	midOrder(root->left);
	printf("%d-", root->key);
	if(root->color == RED)
		printf("RED ");
	else
		printf("BLACK ");
	midOrder(root->right);
}

void preOrder(treeNode *root)
{
	if(root == NULL)
		return;
	printf("%d-", root->key);
	if(root->color == RED)
		printf("RED ");
	else
		printf("BLACK ");
	preOrder(root->left);
	preOrder(root->right);
}


int main()
{
	int select, a;
	treeNode *root = NULL;
	do 
	{
		printf("请输入选择 1--插入，2--查询， 3--删除, 4--输出中序和前序，其他跳出
");
		scanf("%d", &select);
		if (select == 1)
		{
			printf("输入将要插入的值, -1表示结束
");
			while(scanf("%d", &a), a != -1)
			{
				root = rb_insert(root, a);
			}
		}
		else if (select == 2)
		{
			printf("输入将要查询的值, -1表示退出查询
");
			while(scanf("%d", &a), a != -1)
			{
				if(rb_find(root, a) != NULL)
				{
					//printf("找到了
");
				}
				else
					printf("木有找到
");
			}
		}
		else if(select == 3)
		{
			printf("输入将要删除的值, -1表示退出删除
");
			while(scanf("%d", &a), a != -1)
			{
				root = rb_delete(root, a);
			}
		}
		else if(select == 4)
		{
			printf("中序是:
");
			midOrder(root);
			printf("
前序是:
");
			preOrder(root);
			printf("
");
		}
		else break;

	} while (true);
	

	getchar();
	return 0;
}

运行结果，据小雨自己测试没有错误，欢迎大家前来拍砖