由二叉树的前序和中序如何得到二叉树的后序呢?要给出答案,首先得明白什么是前序、中序、后序。
二叉树前序:遍历顺序为,根节点、左子树、右子树;中序:遍历顺序为,左子树、根节点、右子树;后序:遍历顺序为,左子树、右子树、根节点
可以发现,二叉树前序中的第一个节点为树的根节点root,然后找出root在中序里面的位置,就可以把前序和中序分别划分为左、右子树两个部分,然后递归调用即可。
举个例子,前序 5 3 2 4 8 6 10 中序 2 3 4 5 6 8 10
首先,5肯定是二叉树的根节点,然后5在中序里面的位置是3号(从0开始),此位置前面的是左子树中的节点,右面的是右子树的节点,即5 || 3 2 4 || 8 2 6 , 2 3 4 || 5 || 6 8 10,对红色的左子树序列、蓝色的右子树序列继续上述过程,直至结束。
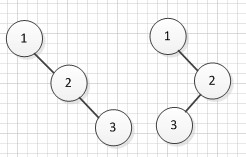
由后序和中序求前序也是像类似的思想。但是仅仅知道前序和后序无法确定二叉的形状。比如前序 1 2 3 后序 3 2 1 则下面两种情况都符合
附二叉树前序和中序生成后序的代码
1 //二叉树 前序和中序得到后序 2 #include <stdio.h> 3 typedef struct node 4 { 5 int key; 6 struct node *left; 7 struct node *right; 8 }treeNode; 9 10 int pre_order[100]; 11 int mid_order[100]; 12 13 treeNode* construct_post_order(int pre_l, int pre_r, int mid_l, int mid_r) 14 { 15 if (pre_r - pre_l < 0) 16 { 17 return NULL; 18 } 19 treeNode *root; 20 root = new treeNode; 21 root->key = pre_order[pre_l]; 22 if (pre_r == pre_l) 23 { 24 root->left = NULL; 25 root->right = NULL; 26 return root; 27 } 28 int index; 29 for (index = mid_l; index <= mid_r; index++) 30 { 31 if (mid_order[index] == pre_order[pre_l]) 32 break; 33 } 34 root->left = construct_post_order(pre_l+1, pre_l+(index-mid_l), mid_l, index-1); 35 root->right = construct_post_order(pre_l+(index-mid_l)+1, pre_r, index+1, mid_r); 36 return root; 37 } 38 39 void post_Order(treeNode *root) 40 { 41 if(root != NULL) 42 { 43 post_Order(root->left); 44 post_Order(root->right); 45 printf("%d ", root->key); 46 } 47 } 48 49 int main() 50 { 51 int n; 52 printf("输入序列的长度 "); 53 scanf("%d", &n); 54 printf("输入二叉树前序 "); 55 for (int i = 0; i < n; i++) 56 scanf("%d", &pre_order[i]); 57 printf("输入二叉树中序 "); 58 for (int i = 0; i < n; i++) 59 scanf("%d", &mid_order[i]); 60 treeNode *root = construct_post_order(0, n-1, 0, n-1); 61 printf("二叉树的后序为 "); 62 post_Order(root); 63 printf(" "); 64 scanf("%d", &n); 65 66 return 0; 67 }