插入排序:直接插入排序,折半插入排序,希尔排序
交换排序:冒泡,快速
选择排序:简单选择排序,堆排序
归并排序
基数排序
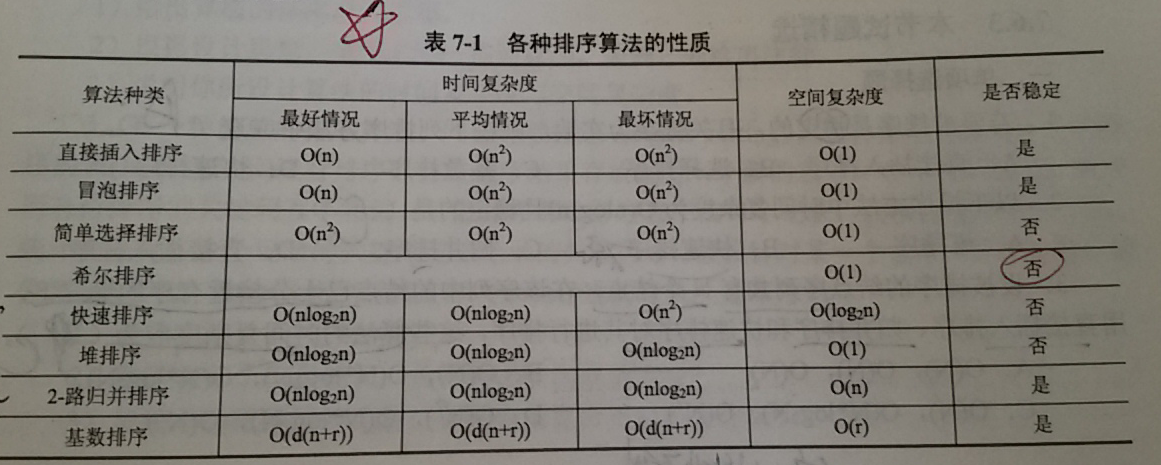
插入排序
void InsertSort(vector<int> &nums) { int i, j; for (int i = 2; i < nums.size(); i++) { if (nums[i] < nums[i - 1]) //如果第i个元素比已排序元素还大就没必要管了,继续下一个 { nums[0] = nums[i]; //哨兵,就是待排序的那个元素,数组中一般用nums[0] for (j = i - 1; nums[j] > nums[0]; j--) nums[j + 1] = nums[j]; //比哨兵大就要向后移动 nums[j] = nums[0]; //找到合适的位置了 } } }
折半插入排序
先折半查找出待插入元素的位置,然后再移动元素
希尔排序
将相距为某一个增量的记录组成一个子序列,使其成为基本有序,所谓基本有序,就是小的关键字基本在前面,大的基本在后面,不大不小的基本在中间
增量序列,要确保最后一个增量值为1
increment = nums.size(); increment = increment / 3 + 1;
实现:相当于直接插入排序的 i 变成increment,外面多了层do while
void ShellSort(vector<int> &nums) { int increment = nums.size(); do { increment = increment / 3 + 1; for (int i = increment; i< nums.size(); i++) { if (nums[i] > nums[i - increment]) { nums[0] = nums[i]; //哨兵 for (int j = i - increment; nums[j] > nums[0]; j -= increment) nums[j + increment] = nums[j]; nums[j + increment] = nums[0]; } } } while (increment > 1); }
冒泡
void BubbleSort(vector<int> &nums) { int n = nums.size(); bool flag = true; //标记是否发生交换 for (int i = 0; i < n - 1 && flag; i++) //外层循环走到倒数第二个元素 { flag = false; for (int j = n - 1; j > i; j--) { if (nums[j] < nums[j - 1]) { swap(nums[j - 1], nums[j]); flag = true; //这一轮有反生交换,就需要下一轮 } } } }
快速排序
STL中的sort三点中值法,取整个序列的头、尾、中央三个位置的元素,以其中值作为枢轴。
int Partition(vector<int> &nums, int low, int high) { int pivot = nums[low]; while (low < high) { while (low < high && nums[high] >= pivot) high--; swap(nums[low], nums[high]); while (low < high && nums[low] <= pivot) low++; swap(nums[low], nums[high]); } return low; } void QuickSort(vector<int> &nums, int low, int high) { int index; if (low < high) { index = Partition(nums, low, high); QuickSort(nums, low, index - 1); QuickSort(nums, index + 1, high); } }
选择排序
void SelectionSort(vector<int> &nums) { int n = nums.size(); for (int i = 1; i < n; i++) { int min = i; for (int j = i + 1; j < n; j++) { if (nums[j] < nums[min]) min = j; } if (i != min) swap(nums[i], nums[min]); } }
堆排序
向n个节点的堆中插入一个新元素的时间复杂度是logn,删除是logn,构建n个记录的初试堆,复杂度是n,最坏情况复杂度是nlogn
归并排序
时间复杂度nlogn,空间复杂度n
1 void MergeSort(vector<int> &data, int low, int high) 2 { 3 if (low < high) 4 { 5 int mid = low + (high - low) / 2; 6 MergeSort(data, low, mid); //排序右侧数组 7 MergeSort(data, mid + 1, high); //排序左侧数组 8 Merge(data, low, mid, high); //合并两个已排序的数组 9 } 10 } 11 //合并两个已排序数组 12 void Merge(vector<int>& data, int low, int mid, int high) 13 { 14 vector<int> temp_data = data; 15 int i = low; 16 int j = mid + 1; 17 int k = low; 18 while (i < mid&&j < high) 19 { 20 if (temp_data[i] < temp_data[j]) 21 data[k++] = temp_data[i++]; 22 else 23 data[k++] = temp_data[j++]; 24 } 25 while (i <= mid) 26 data[k++] = temp_data[i++]; 27 while (j <= high) 28 data[k++] = temp_data[j++]; 29 }