【NOIP1999】【洛谷P1020】导弹拦截

问题描述

 输入格式

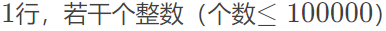
 输出格式

 样例输入

389 207 155 300 299 170 158 65

样例输出

6

2

题解

本题有两个问，我们先来解决第一问

我们用a[i]表示第i个导弹的高度

一套导弹系统能拦截的导弹序列的高度是非上升的，要求最多能拦截的导弹，就是给定数列的最长不上升子序列

我们有一个朴素的n²动规算法

设f[i]表示前i个数的最长不上升子序列长度，易得f[i]=max(f[j])+1(1≤j<i且a[i]≤a[j])

但是导弹个数最多达到10⁵，这样会TLE

考虑优化

显然一个数列中有多个长度不等的不上升子序列，而我们只想知道最长不上升子序列的长度，其它不上升子序列的长度可以忽略，于是我们可以用一点贪心的思想，只存储最长不上升子序列的长度

我们用f[len]来存储最长不上升子序列，其中len表示最长不上升子序列的长度

假设对于数组中前i个数，已找到长度为j的最长不上升子序列，对于第i+1个数a[i+1]，

若a[i+1]不大于当前最长不上升子序列的最后一个数，即a[i+1]≤f[j]，显然把a[i+1]接在f[j]后面可以增大当前最长不上升子序列的长度；如果a[i+1]>f[j]，我们就用a[i+1]更新已知的最长不上升子序列，我们希望不上升子序列尽可能长，所以我们需要不上升子序列前面部分的元素尽可能大，这样后面才能接上尽可能多的元素，所以每一次对已知最长不上升子序列的更新都要使序列中某个元素变大并且不破坏不上升的性质。考虑到已知最长不上升子序列是一个非递增序列，我们可以用二分找到序列中比a[i+1]小的第一个数的位置，并用a[i+1]把这个数换掉，这样既满足了把一个元素变大，又不会破坏不上升的性质，因为由二分的条件知这个位置前面的数一定比a[i+1]大且后面的数一定不比a[i+1]大。

这样就把时间复杂度降到了nlogn

---

 再来看第二问

要用最少的拦截系统拦截所有导弹

用到和前面相似的思想，要充分利用每一个系统，使得每个系统能拦截的导弹尽可能多

假设对于前i个导弹，已经用了t个系统，对于第i+1个导弹，要尽量不增加新的系统，如果当前有系统可以拦截这个导弹（当前已找到的t个不上升子序列中存在序列的最后一个元素不小于a[i+1]），显然就用这个系统拦截导弹，如果有多个系统满足条件，考虑到要使后面能拦截的导弹尽可能多，我们选择满足条件的系统中（序列最后一个元素比a[i+1]大）最后一个元素最小的系统来拦截这个导弹，这样如果后面还有比a[i+1]高的导弹就可以用系统来拦，如果拦a[i+1]的系统不是最后一个元素最小的，后面出现比a[i+1]高的本来可以被这个系统拦截的导弹就因为这个系统拦截了a[i+1]而拦截不了，从而造成浪费

#include <algorithm>
#include <cstdio>
int a[100005],f[100005],n,h[100005];
bool cmp(const int& a,const int& b)
{
    return a>b;
}
int main()
{
    n=1;
    while (~scanf("%d",&a[n])) n++;
    n--;
    int i,j,len=1;
    f[1]=a[1];
    for (i=2;i<=n;i++)
    {
        if (a[i]<=f[len]) f[++len]=a[i];
        else
        {
            j=std::upper_bound(f+1,f+len+1,a[i],cmp)-f;
            f[j]=a[i];
        }     
    }
    printf("%d
",len);
    int t=1,s,x;
    h[1]=a[1];
    for (i=2;i<=n;i++)
    {
        s=0;  x=2e9;
        for (j=1;j<=t;j++)
          if (a[i]<=h[j] && h[j]<x)
          {
              s=j;  x=h[j];    
          }
        if (s!=0) h[s]=a[i];
        else h[++t]=a[i];  
    }     
    printf("%d",t);
    return 0; 
}