看名字很难,实际上贼简单...
本蒟蒻瑟瑟发抖,请大佬们不要喷...
写的有点长,如果觉得读不下去...
肯定读的下去,我写得多通俗易懂啊!
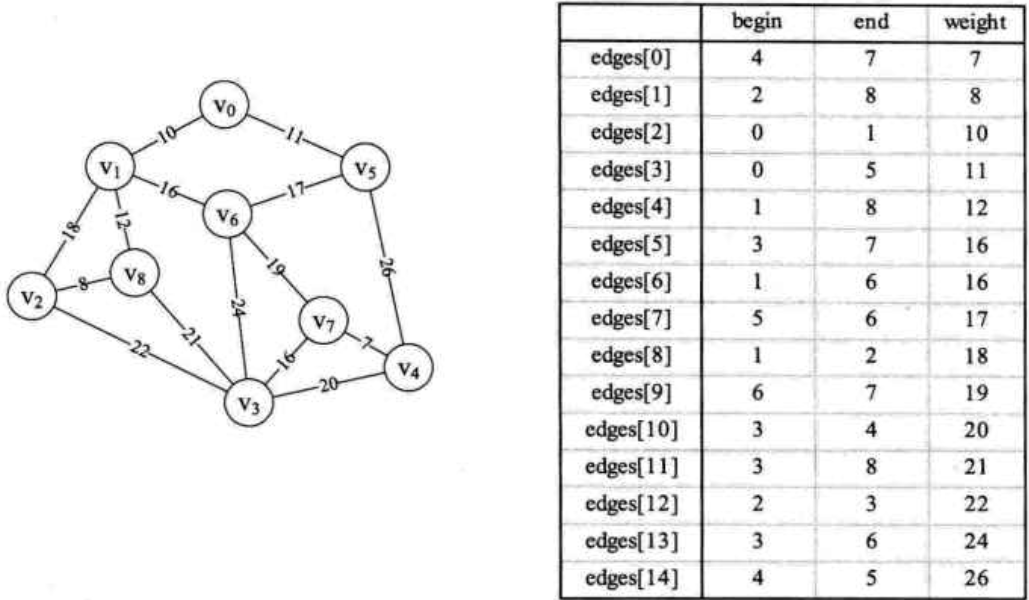
不要管右面的表格...看左面的图...好,让我们开始:
PS:n代表点的个数,m代表边的个数
Part 1:邻接矩阵
先列出来矩阵,然后慢慢的讲
v0 v1 v2 v3 v4 v5 v6 v7 v8
v0 1 1 0 0 0 1 0 0 0
v1 1 1 1 0 0 0 1 0 1
v2 0 1 1 1 0 0 0 0 1
v3 0 0 1 1 1 0 0 1 1
v4 0 0 0 1 1 1 0 1 0
v5 1 0 0 0 1 1 1 0 1
v6 0 1 0 1 0 1 1 1 0
v7 0 0 0 1 1 0 1 1 0
v8 0 1 1 1 0 0 0 0 1
(1,0可以用连接这两个点的边权代替)
有横列,有纵列,交点代表横轴和纵轴所代表的点能否直接联通
直接联通的意思就是有一条边直接连着它们而不是通过别的点与边相连
0代表不能直接联通,而1代表能直接联通
好啦,现在如果要判断某两个点能否联通,开始搜索即可
找能和点1联通的所有点然后接着搜即可...(时间复杂度为n的平方)
或者使用并查集(合并查询)也可以...
但是很慢,真的很慢,时空复杂度都很大...
好啦,那我们该怎么办呢?有请Part 2
Part 2 邻接表
它可以大大地减小时间复杂度(时间复杂度为m)
但是减小不了空间复杂度...
先列出来表,然后慢慢的讲
v0 v1 v2 v3 v4 v5 v6 v7 v8
v0 v0 v1 v2 v3 v0 v1 v3 v1
v1 v1 v2 v3 v4 v4 v3 v4 v2
v5 v2 v3 v4 v5 v5 v5 v6 v3
v6 v8 v7 v7 v6 v6 v7 v8
v8 v8 v8 v7
第一行代表每个点
第一行点下面的点代表它能直接联通的点
你看,搜每个点邻接矩阵必须搜七次
而邻接表只需要搜三到四次即可
大大减少了时间复杂度
尤其是用BFS搜点的时候,所需的时间复杂度更小
但是空间复杂度仍然很大...
小心开long long会原地爆炸...
所以,有请Part 3
Part 3 链式前向星
时间复杂度与邻接表一样,均为m
但它大大优化了空间复杂度
(不要笑话我只会用“大大的”这种形容词)
那么它的原理是什么呢?
让我们代入情景:
我们要去一个世界顶级的珠宝商场
卖的东西很好,当然也很贵
但我们的钱包比自己的脸还干净
那怎么办呢?怎么办呢?
闭上双眼!两只手放在膝盖上!默念三遍:
我很有钱!
我很有钱!
我很有钱!
好了,我现在很有钱!
穿着你妈你(阿玛尼),挎着卡地亚
我们走了进去,领到了一张很小的纸(只能写一个人的名字)
(这个商店一个人一次只能购买一件珠宝)
(而且入场费灰常贵)
一看,啊!我的纯钛合金24K大狗眼被珠宝的闪光晃瞎了!
背着手信步前进,我要买这个!那个更好!这个太棒了!
但是珠宝上也有一张很小的纸(只能写一个人的名字)
而且这张纸上已经有别人的名字了
那我们应该怎么办?
把他的名字擦了,写上我的名字!
我觉得持这种想法的人你很坏
但你确实对了,不过只对了一半
还少一步:在你的纸上写下你擦掉的人的名字
这样我们才有诚信嘛,对不对?
好啦,假设有1,7,9三个人买同样的珠宝
主办方一看纸上有9的名字
就去问9,说你擦了谁的?
9说我擦了7的
主办方再屁颠屁颠地去问7,说你擦了谁的
7说我擦了1的
主办方去问1,1说我没有擦别人的
好啦,搜索到此为止,1,7,9三个人买了这个珠宝
主办方把三个珠宝包起来送给他们就行啦!
这就是链式前向星的基本原理!
我们会开一个结构体和一个数组
struct Edge{
int next;
int to;
int x;
}edge[(自己写大小)];
head[(自己写大小)];
int cnt;
next存的是当前边所指向的下一条边
to存的是当前边所指向的目标节点
w存的是当前边的权值
edge[m]表示第m个边
head[m]表示第m个点的最后一条边,以确定寻找的边界
cnt存的是总边数
这样一个神奇的图就建出来啦!
建图操作:
void add(int x,int y){
edge[++cnt].to = y;
edge[cnt].nxt = head[x];
head[x] = cnt;
}(可以双向建图)
那么这个操作什么意思呢?

看这个图!(所有数组从1开始)
(to与next有m个元素,因为有m个边)
(head有n个元素,因为有n个边)
(前缀v是用来理解的,当你懂了以后可以把v去掉)
比如要在v1与v8之间连一条边
由v8指向v1
那么需要add(v8,v1)
此时cnt = 1
首先要在to[1]内存一个v1(就是数字1)
此时head[v8] = 0(就是数组第8位)
则next[1] = 0
head[v8] = 1
即
to[v1 0 0 0 0 0 0 0 0 0。。。](后面的元素用省略号代替)
next[0 0 0 0 0 0 0 0 0 0。。。]
head[0 0 0 0 0 0 0 1 。。。]
双向建图:
此时cnt = 2
首先要在to[2]内存一个v8
此时head[v1] = 0
则next[2] = 0
head[v1] = 2
即
to[v1 v8 0 0 0 0 0 0 0 0。。。]
next[0 0 0 0 0 0 0 0 0 0。。。]
head[2 0 0 0 0 0 0 1 。。。]
再在v1与v2之间连一条边
由v2向v1
那么需要add(v2 ,v1)
此时cnt = 3
首先要在to[3]内存一个v1
此时head[v2] = 0
则next[3] = 0
head[v2] = 3
即
to[v1 v8 v1 0 0 0 0 0 0 0。。。]
next[0 0 0 0 0 0 0 0 0 0。。。]
head[2 3 0 0 0 0 0 1 。。。]
双向建图:
此时cnt = 4
首先要在to[4]内存一个v2
此时head[v1] = 2
则next[4] = 2
head[v1] = 4
即
to[v1 v8 v1 v2 0 0 0 0 0 0。。。]
next[0 0 0 2 0 0 0 0 0 0。。。]
head[4 3 0 0 0 0 0 1 。。。]
什么意思呢?
head与next里存的是数的编号
to里存的是真实的点
真实的点在to里的编号(比如v8编号为2,v2编号为4)
就是head数组里的另一个被它擦掉的数在to里的编号
(就相当于被你擦掉并写在你手里的纸上的编号)
先举这么多栗子(例子)
当我要查询v1直接连接的边(初边)的时候
先查head[v1] = 4
那么就查to[head[v1]]即to[4] = v2
证明v2与v1相连
v2在to里的编号是4
再找next[4] = 2
即在v2前面被擦掉的数在to里的编号是2
那么就查to[2] = v8
证明v8与v1相连
v8在to里的编号是2
再找next[2] = 0
意思就是没有数被它擦掉了
搜索结束
与v1相连的点输入了v2,v8
查找的结果也是v2,v8正确
那么链式前向星的思想与代码就讲完了!
感谢lyn大佬与zyr大佬的帮助!
小伙伴们都懂了吗?
学习信息竞赛的路还很长,但要坚持下去。
要坚信:真金不怕火炼!
——沃兹基硕德
(我自己说的)