p1612

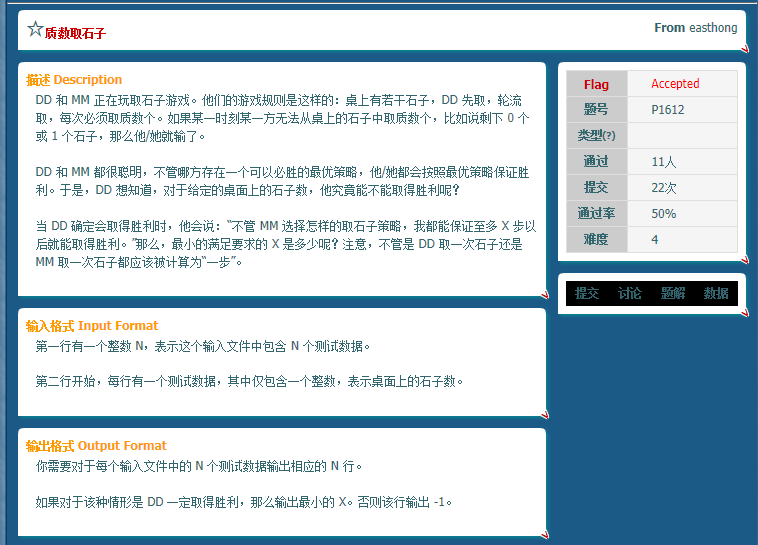
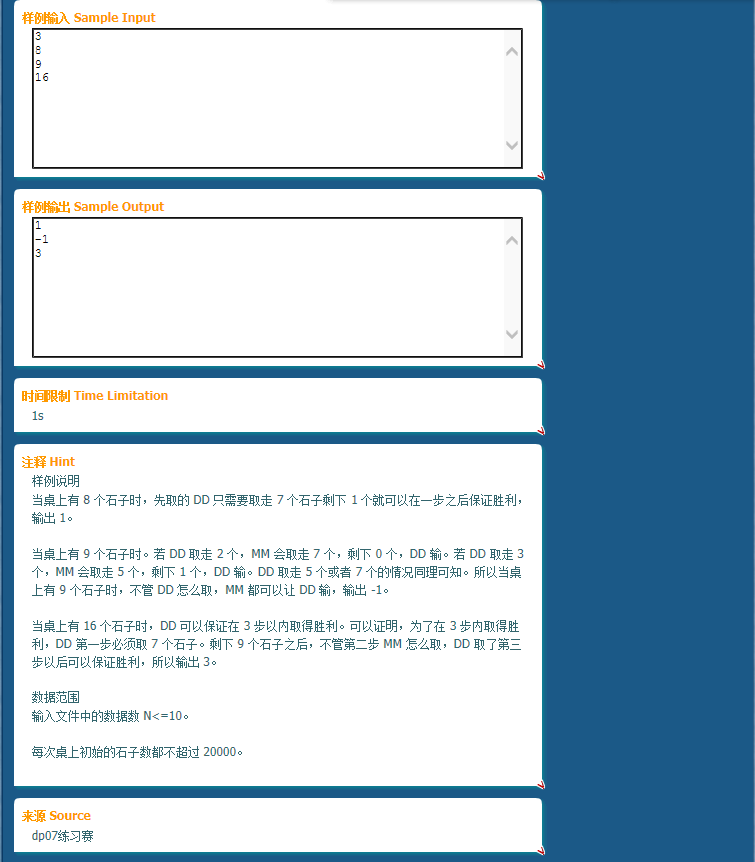
大大和MM玩游戏~~

好像博弈论整个都是一个大dp,而转移连我都会.步数好好考虑一下也可以想到怎么搞,为什么这么少人A.

先来一个素数筛模板,只要筛到十组数组中的最大值就好.得到素数个数sum与各个素数prime[i];

然后对于每个i取石子时我们减去能减的素数,一旦拿掉某个素数个数后变成了必输态就一定是必胜态,赋值为1.如果最后也没有见到必输态就不管了.第一问解决.

关于步数的问题,考虑如果我必胜的状态一定希望自己取的步数最小,必输的状态希望对方取的步数最多(争强好胜),那么对方也是一样的.只有在当前必胜且下一步必输或当前必输且下一步必胜的时候才能转移.当前必胜且下一步必输是取min(d[i],d[i-prime[f]]+1);当前必输且下一步必胜时取max(d[i],d[i-prime[f]]+1);

最后判断flag后输出-1或d[o[i]]即可.

using namespace std;
int i,f;
int n,maxx;
int v[10000010],sum,prime[10000];
int flag[100000],o[100],d[1000000];
int main()
{
    cin>>n;
    flag[2]=flag[3]=1;
    for(i=1;i<=n;i++)
        o[i]=read(),maxx=max(maxx,o[i]);
    for(i=2;i<=maxx;i++)
    {
        if(!v[i])
        {
            sum++;
            v[i]=i;
            prime[sum]=i;
        }
        for(f=1;f<=sum;f++)
        {
            if(prime[f]>v[i]||prime[f]>maxx/i)break;
            v[i*prime[f]]=prime[f];
        }
    }
    for(i=2;i<=maxx;i++)
        for(f=1;f<=sum;f++)
            {
                if(prime[f]>i)
                    break;
                if(!flag[i-prime[f]])
                {
                    flag[i]=1;
                    break;
                }
            }
    for(i=2;i<=maxx;i++)
    {
        for(f=1;f<=sum;f++)
        {
            if(i<prime[f]) 
                break;
            if(flag[i]&&!flag[i-prime[f]]) 
                if(d[i]==0) 
                    d[i]=d[i-prime[f]]+1;
                else 
                    d[i]=min(d[i],d[i-prime[f]]+1);
            else 
                if(!flag[i]&&flag[i-prime[f]])                        
                { 
                    if(d[i]==0) 
                        d[i]=d[i-prime[f]]+1;
                    else   
                        d[i]=max(d[i],d[i-prime[f]]+1);
                }
        }
    }
    for(i=1;i<=n;i++)
    {        
        if(!flag[o[i]]) 
            write(-1);
        else
            write(d[o[i]]);
        putchar(10);
    }
}