p1884

十月的停课集训开始了,祝我顺利.

半上午时间搞了这道题,感觉非常的值得.

和当年做的某两题题目类似吧,但是又有很大区别.可以想到两个点间的距离是max(Δx,Δy);

可以很快想到暴力算法:枚举每对点并计算距离后相加.但是本题的点数是<=m*n的,这个算法就是n*n*m*m,GG

刚开始没有注意到可以向四面八方跑,只能上下左右的话我会写动态规划:记录每一列和每一行的点数.用m*n算出所有点到(1,1)的距离和d[1][1],那么d[i][1]=d[i-1][1]+第i-1行及以上的点数-第i行及以下的点数,因为上面的每个点到这个点的距离比之前多了1,而这一行与下面的点到这个点距离都小了1.而d[i][f]=d[i][f-1]+第f-1列及以前的点数-第f列及以后的点数.原理和刚才一样.

然而本题要求斜着走也为1,向下走的时候就不一定谁要多1谁要小1了,所以改怎么办呢?

我们来画一个图

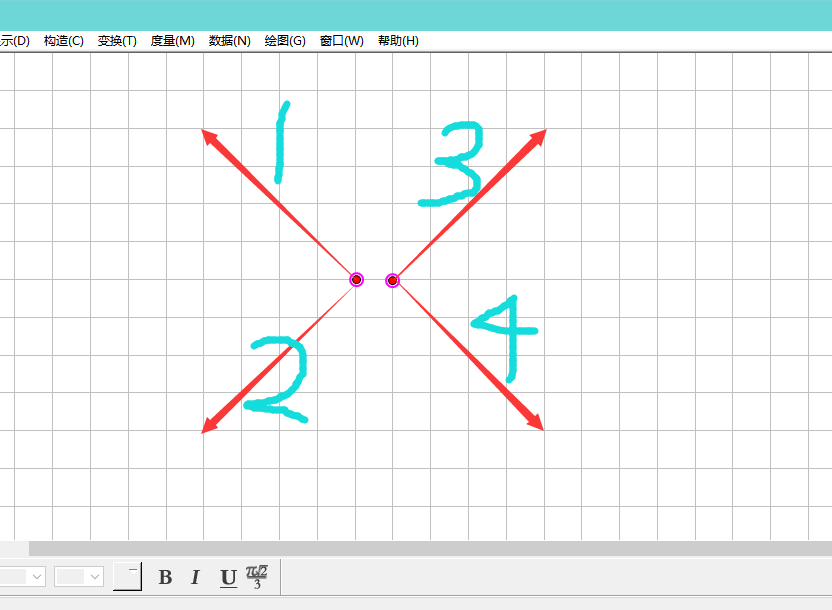
还是来说向右转移的方法.如果其他的点对于当前点和左边的点全部都是Δy大于Δx的,那么向右转移后就没有任何变化.如果左边有zuo个点Δx大于Δy(即距离由Δx决定),那么向右移动1位后距离就会加zuo,右边有you个点Δx大于Δy,距离会减you.

d[i][f]=d[i][f-1]+zuo-you;

那么这个"zuo"."you"如何得到呢?我们预处理四个数组xie1[i][f],xie2[i][f],xie3[i][f],xie4[i][f]表示点(i,f)在上图的四个方向上的点的总数(预处理复杂度也是m*n的),那么

zuo[i][f]=zuo[i][f-1]+xie1[i][f-1]+xie2[i][f-1];
you[i][f]=you[i][f-1]-xie3[i][f-1]-xie3[i][f-1];
if(o[i][f]!='.')zuo[i][f]--,you[i][f]--;

(这里只是用下标表示一下,实际上不用专门给他俩开数组的)

而上下的转移也是类似的过程.

这样,就一直使用m*n的循环完成了本题.具体实现细节可以看代码.

using namespace std;
long long i,f,shang,xia,zuo,you;
char t;
long long n,m;
long long o[1010][1010],ans[1010][1010],sum;
long long xie1[1010][1010],xie2[1010][1010],xie3[1010][1010],xie4[1010][1010];
int main()
{
    cin>>n>>m;
    for(i=1;i<=n;i++){
        for(f=1;f<=m;f++){
            cin>>t;
            if(t=='M')
                o[i][f]=1;
        }
    }
    for(i=1;i<=n;i++){
        for(f=1;f<=m;f++){
            xie1[i][f]=xie1[i-1][f-1];
            xie3[i][f]=xie3[i-1][f+1];
            if(o[i][f]==1){    
                ans[1][1]+=max(i-1,f-1);
                xie1[i][f]++;
                xie3[i][f]++;
                xie2[i][f]++;
                xie4[i][f]++;
            }
        }
    }
    for(i=n;i>=1;i--){
        for(f=1;f<=m;f++){
            xie2[i][f]+=xie2[i+1][f-1];
            xie4[i][f]+=xie4[i+1][f+1];
        }
    }    
    
//处理ans[i][1];
    for(i=2;i<=n;i++)
        xia+=xie4[i][1];
    for(i=2;i<=n;i++){
        shang+=xie3[i-1][1];
        ans[i][1]=ans[i-1][1]+shang-xia;
        xia-=xie4[i][1];
    }
//处理ans[i][f];
    for(i=1;i<=n;i++){
        you=zuo=0;
        for(f=2;f<=m;f++){        
            you+=xie3[i][f]+xie4[i][f];
            if(o[i][f]==1)
                you--;
        }
        for(f=2;f<=m;f++){
            zuo+=xie1[i][f-1]+xie2[i][f-1];
            if(o[i][f-1]==1)
                zuo--;
            ans[i][f]=ans[i][f-1]+zuo-you;
            you-=xie3[i][f]+xie4[i][f];
            if(o[i][f]==1)
                you++;
        }
    }
    for(i=1;i<=n;i++){
        for(f=1;f<=m;f++){
            if(o[i][f]==1)
                sum+=ans[i][f];
        }
    }
//每个距离都被算了两次
    cout<<sum/2<<' ';
}

人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 
人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
(人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是
( 人类的本质是( )。
A.复读机
B.鹦鹉
C.+①
D.人类的本质是( )。
)。
 )。
)。
)。
)。
)。
)。
)。
)。
)。
)。
)。
)。