差分是一种很神奇的方法、思路。它将一个数组a[]改写成为a[i]=o[i]-o[i-1],然后可以达到区间修改等许多神奇操作。
考虑长为n的数组a[i]给出m次修改,每次修改区间[l,r],最后问你一个位置a[k]的大小.怎么写?
呵水题,先把修改存起来然后记录下k.再回去看每个修改有没有对a[k]动手.复杂度m.
当然了,上面的题是说着玩的.
然后来考虑如果m次修改最后问原数组a[i]每个元素的大小怎么写?
我们考虑设立一个差分数组c[i]=a[i]=a[i-1];这样跑完一遍后可以得到c[i]表示原数组的相邻元素的差值.然后考虑在区间修改的时候只有区间两个端点附近的两个节点改变了,区间内部的c并没有改变.也就是说对于区间[l,r]+=add;我们只需要对c数组做两次操作:c[l]+=add,c[r+1]-=add;这样每次修改就是O(1)的了.然后是最后还原原数组的时候只需要跑一遍a[i]=a[i-1]+c[i]就好了.
然后来考虑如果m次修改中间穿插有求a[k]的大小的题怎么写?
假如修改还按原来的写,询问的时候显然a[k]=∑c[1...k];这个复杂度是n的.好在我们有众多的高级数据结构.什么树状数组什么线段树什么分块都能做到logn或根号n的.
然后来考虑如果m次修改中间穿插有求a[k]和∑a[1....k]的怎么写?
艹我怎么知道啊只需要写两个树状数组或者一个线段树就好了.
先来一个模板水题。
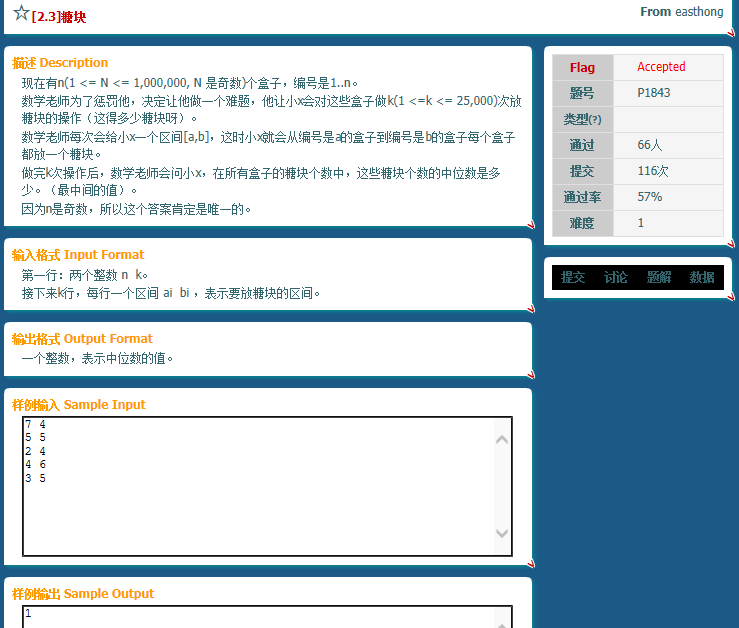
区间修改的时候已经在回忆差分了,然后发现最后要求的是中位数,裸差分的话修改一共k,回归原数组是n,排一下序也就是n*logn,很稳。
那么int一个查分数组a,输入两端点后把c[x]++,c[y-1]--。回归原数组时a[i]=a[i-1]+c[i],想到甚至可以用滚动数组就可以直接覆盖之前的点和自己,也就是o[i]+=o[i-1],此时o[i-1]已经是原数组,加上查分数组也变成了原数组,一次类推。回归完后可以调用sort,一个数组解决问题。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<cmath> 6 #include<string> 7 #include<algorithm> 8 #include<vector> 9 #include<map> 10 #include<stack> 11 #include<queue> 12 #include<deque> 13 #include<set> 14 using namespace std; 15 int i,tx,ty; 16 int a[1000010],n,k; 17 int main() 18 { 19 ios::sync_with_stdio(false); 20 cin.tie(NULL); 21 cout.tie(NULL); 22 //freopen("123.in","r",stdin); 23 cin>>n>>k; 24 for(i=1;i<=k;i++) 25 { 26 cin>>tx>>ty; 27 a[tx]++; 28 a[ty+1]--; 29 } 30 for(i=1;i<=n;i++) 31 a[i]+=a[i-1]; 32 sort(a+1,a+1+n); 33 cout<<a[n/2+1]; 34 }
再水一个noip2018Day1T1和noip2013Day2T1;