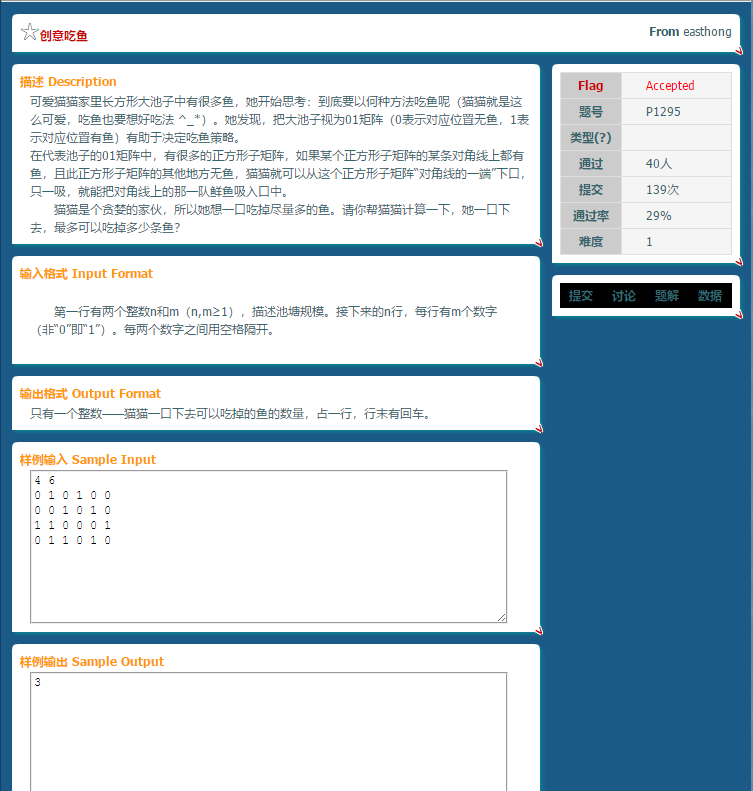
这道题之前听LZD说过,困扰了他好久。那困扰我两天应该不丢人吧嘿嘿嘿。
---------------------------------------------------------这部分是误解,觉得智障的可以直接跳到下一个部分了-----------------------------------------------------------------------------------------------------
首先我知道可以用暴力搜索判断每一个正方形的对角线以外的地方有没有鱼(我还以为只要满足这个就可以了,没想到对角线上的鱼也要保证连续)。这个方法的复杂的原因在于枚举正方形与判断对角线以外的地方有没有1.
抱着这样的态度我开始了优化:输入时如果o[i][f]为鱼就把sumx[i][f]++,sumy[f][i]++;否则sumx[i][f]=sumx[i][f-1],sumy[f][i]=sumy[f][i-1];这样弄完之后sumx[i][f]表示在第i行的前f个地方鱼的个数,sumy[f][i]表示第f列中前i行鱼的个数。然后在下面的遍历中判断sumx与sumy即可在复杂度为1的时间内得出(i,f)与(x,y)中间是否有鱼。
遍历时我以为是一个贪心,如果中间出现有鱼就不管了。而对角线断了也能继续(捂脸),真是菜的真实。

1 using namespace std; 2 int i,f,n,m,now,ans; 3 bool o[2600][2600],flag[2600][2600]; 4 int sumx[2600][2600],sumy[2600][2600]; 5 void youxia(int x,int y)//不论何时开始了函数,起点总是i,f 6 { 7 now=flag[x][y]=1; 8 for(x++,y++;x<=n&&y<=m;x++,y++) 9 { 10 if(o[x][y]) 11 { 12 if(sumx[x][y]==sumx[x][f-1]+1&&sumy[y][x]==sumy[y][i-1]+1) 13 { 14 now++; 15 } 16 else break; 17 } 18 else 19 { 20 if(sumx[x][y]!=sumx[x][f-1]||sumy[y][x]!=sumy[y][i-1]) 21 break; 22 } 23 flag[x][y]=1; 24 } 25 ans=max(ans,now); 26 for(x=1;x<=n;x++) 27 { 28 for(y=1;y<=m;y++) 29 cout<<flag[x][y]<<' '; 30 cout<<endl; 31 } 32 cout<<endl; 33 return ; 34 } 35 void zuoxia(int x,int y) 36 { 37 now=flag[x][y]=1; 38 for(x++,y--;x<=n&&y<=m;x++,y--) 39 { 40 if(o[x][y]) 41 { 42 if(sumx[x][y]==sumx[x][f]&&sumy[y][x]==sumy[y][i-1]+1) 43 { 44 now++; 45 } 46 else break; 47 } 48 else 49 { 50 if(sumx[x][y-1]!=sumx[x][f]||sumy[y][x]!=sumy[y][i-1]) 51 break; 52 } 53 flag[x][y]=1; 54 } 55 ans=max(ans,now); 56 return; 57 } 58 int main() 59 { 60 //freopen("123.in","r",stdin); 61 //freopen("123.out","w",stdout); 62 cin>>n>>m; 63 for(i=1;i<=n;i++) 64 { 65 for(f=1;f<=m;f++) 66 { 67 cin>>o[i][f]; 68 if(o[i][f]) 69 { 70 sumx[i][f]=sumx[i][f-1]+1; 71 sumy[f][i]=sumy[f][i-1]+1; 72 } 73 else 74 { 75 sumx[i][f]=sumx[i][f-1]; 76 sumy[f][i]=sumy[f][i-1]; 77 } 78 } 79 } 80 81 for(i=1;i<=n;i++) 82 { 83 for(f=1;f<=m;f++) 84 { 85 if(o[i][f]&&!flag[i][f]) 86 { 87 88 youxia(i,f); 89 } 90 } 91 } 92 memset(flag,0,sizeof(flag)); 93 for(i=1;i<=n;i++) 94 { 95 for(f=1;f<=m;f++) 96 { 97 if(o[i][f]&&!flag[i][f]) 98 { 99 zuoxia(i,f); 100 } 101 } 102 } 103 cout<<ans; 104 } 105
-----------------------------------------------------------------------------------------------------以下是正解了---------------------------------------------------------------------------------------------------------------------------------------------------------
那么怎样改才正确呢?我先是把我代码里的else删掉两个,只要不是1就停下来。想了想应该是十分正确的,保证了每个1只跑了一次zuoxia()与youxia(),复杂度是1的个数。但是交上去的话会有一组数据过不了。
这是因为虽然在之前的起点中有个点旁边有1,但在别的起点就不一定了。因此不能用flag记录是否已经跑过,这并不是一个贪心!
例如: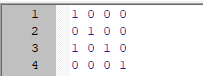
这个小小方阵中第一个1为起点会使第二个1的flag改为1,因此不能再做起点,在第三个点处停下,得出的答案是2。但答案却是以第二个1为起点的三个1。因此这种方法是错误的。
到底是要复杂度呢还是AC呢?考场上就不要再改了,能过很多组数据了(oj上能得90分) 。但在本校oj就可以浪一下了,删掉所有flag后交了一遍,竟然AC了,也就是最大的数据多了几十毫秒而已,没有那么恐怖。
最后总结一下题解:预处理出每一列前每行和每一行前每列的1的个数,对所有的1跑两个循环,如果新拓展到的点有1就停下,如果在向下不是1也停下,更新答案。
1 #include <cstdio> 2 #include <iostream> 3 #include <cmath> 4 #include <string> 5 #include <cstring> 6 #include <algorithm> 7 using namespace std; 8 inline int read() 9 { 10 int x=0; 11 char ch=getchar(); 12 while(ch>'9'||ch<'0') 13 ch=getchar(); 14 while(ch>='0'&&ch<='9') 15 { 16 x=(x<<1)+(x<<3)+ch-'0'; 17 ch=getchar(); 18 } 19 return x; 20 } 21 int i,f,n,m,now,ans; 22 bool o[2600][2600],flag[2600][2600]; 23 int sumx[2600][2600],sumy[2600][2600]; 24 void youxia(int x,int y) 25 { 26 now=1; 27 for(x++,y++;x<=n&&y<=m;x++,y++) 28 { 29 if(o[x][y]) 30 { 31 if(sumx[x][y]==sumx[x][f-1]+1&&sumy[y][x]==sumy[y][i-1]+1) 32 { 33 now++; 34 } 35 else break; 36 } 37 else 38 break; 39 } 40 ans=max(ans,now); 41 42 return ; 43 } 44 void zuoxia(int x,int y) 45 { 46 now=1; 47 for(x++,y--;x<=n&&y>=0;x++,y--) 48 { 49 if(o[x][y]) 50 { 51 if(sumx[x][y]==sumx[x][f]&&sumy[y][x]==sumy[y][i-1]+1) 52 { 53 now++; 54 } 55 else break; 56 } 57 else break; 58 } 59 ans=max(ans,now); 60 return; 61 } 62 int main() 63 { 64 //freopen("123.in","r",stdin); 65 //freopen("123.out","w",stdout); 66 cin>>n>>m; 67 for(i=1;i<=n;i++) 68 { 69 for(f=1;f<=m;f++) 70 { 71 o[i][f]=read(); 72 if(o[i][f]) 73 { 74 sumx[i][f]=sumx[i][f-1]+1; 75 sumy[f][i]=sumy[f][i-1]+1; 76 } 77 else 78 { 79 sumx[i][f]=sumx[i][f-1]; 80 sumy[f][i]=sumy[f][i-1]; 81 } 82 } 83 } 84 for(i=1;i<=n;i++) 85 { 86 for(f=1;f<=m;f++) 87 { 88 if(o[i][f]) 89 { 90 youxia(i,f); 91 } 92 } 93 } 94 for(i=1;i<=n;i++) 95 { 96 for(f=1;f<=m;f++) 97 { 98 if(o[i][f]) 99 { 100 zuoxia(i,f); 101 } 102 } 103 } 104 cout<<ans; 105 }
那么这道题与动态规划有什么关系呢?
我也不知道……先预处理前缀和后遍历,没有一点点优化……
