并查集与并查集模板

　　并查集  就是不像图论那样关注节点间如何连接，只考虑最最上面的一个节点，从而快速的判断两个节点的关系。

　　实际实现时维护一个fa[n]数组记录父节点，n为节点数量++，初始化所有父节点都为自己。输入每条边，把两个节点的父节点改为一个。然后就可以在复杂度为1的时间内判断两个节点是否在同一个连通块内。搜索所有fa[]里fa[i]仍==i的节点数量即为这个图中连通块的总数。

　　然而题目一般不会给这么裸的题(吧)，我们还可以维护其他数组来记录其他一些情报，比如下面1698中维护的据根节点距离。

　　可以在读题是注意思考题目询问的是什么。并查集对于查询节点是否属于某一集合非常的擅长。

　　然后就是一些例题与模板。

p1699 

　　

　　这就是巨裸的并查集的题了，把模板往上一贴就过了。

再来看一下这道题

不要在意为什么一天带一只手套。x_i与y_i就是要求这两个手套颜色相同。而手套只染色一次，就是T只表示数据组数，与决策无关。

那么这道题就可以把每个x_i与y_i合并，然后再跑一边fa[]记录fa[i]==i的组数sum，它就是手套中要求颜色相同的组数，组的内部一样，外部随便组合，共有m^sum个方案数。

 上并查集，上快速幂，此题可解。反正你们也遇不到这题，就不给代码了。

　p1698 银河英雄传

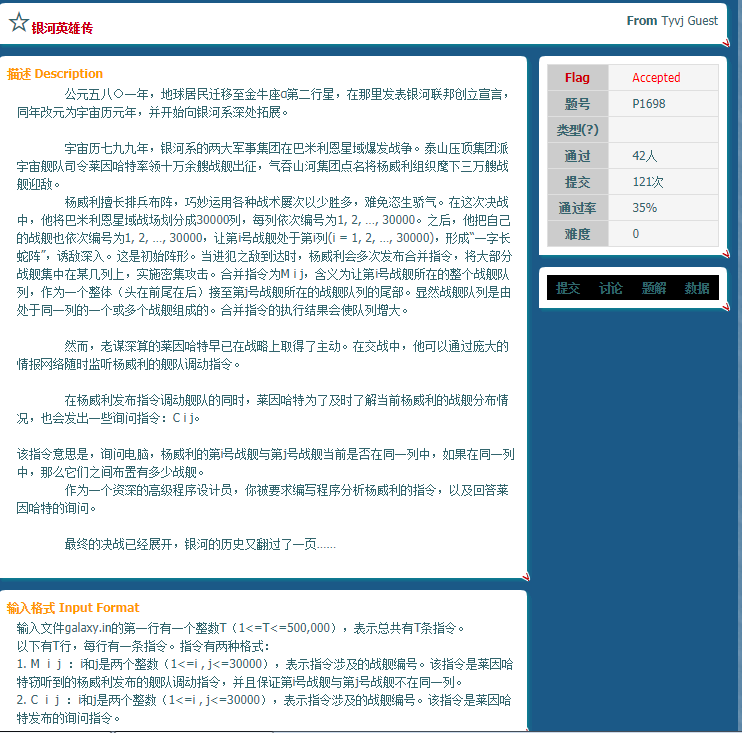
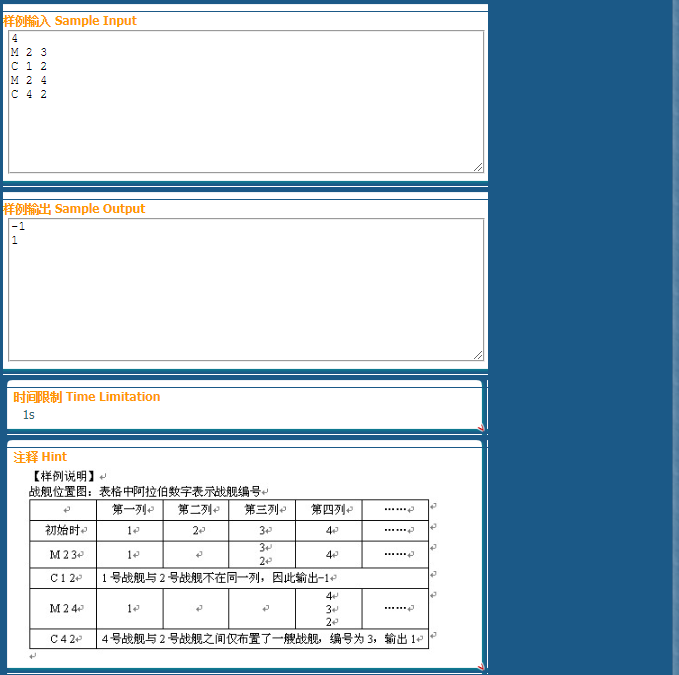
　　这道题，我们除了维护节点的父亲以外，再维护每个战舰到自己父亲的距离before和自己带领的战舰长度after。当询问两个战舰距离时，如果父亲不一样，那就算了。如果一样，那就输出abs(before[a]-before[b])。而在合并的时候，总是令x的父亲为y，更新他们父亲的after与before。

　　丢出代码

using namespace std;
int M=30010;
int T,t1,t2,f1,f2;
int father[30010],before[30010],after[30010];
char temp;
int getfather(int xx)
{
    int yy=father[xx];
    if(yy!=xx)
    {
        father[xx]=getfather(yy);
        before[xx]+=before[yy];
    }
    return father[xx];
}
void merge(int xx,int yy)//xx.head to yy.tail
{
    f1=getfather(xx),f2=getfather(yy);
    father[f1]=f2;
    before[f1]=after[f2];
    after[f2]+=after[f1];
}
int main()
{ios::sync_with_stdio(false);
//freopen("123.in","r",stdin);
//freopen("123.out","w",stdout);
    for(int i=1;i<M;i++)
        father[i]=i,before[i]=0,after[i]=1;
    cin>>T;
    for(int i=1;i<T;i++)
    {
        cin>>temp>>t1>>t2;
        if(temp=='M')
            merge(t1,t2);
        else
        {
            f1=getfather(t1),f2=getfather(t2);
            if(f1!=f2)
                cout<<-1<<endl;
            else
                cout<<abs(before[t1]-before[t2])-1<<endl;
        }
    }
        cin>>temp>>t1>>t2;
        if(temp=='M')
            merge(t1,t2);
        else
        {
            f1=getfather(t1),f2=getfather(t2);
            if(f1!=f2)
                cout<<-1;
            else
                cout<<abs(before[t1]-before[t2])-1;
        }

    return 0;
}

 它有一个重要应用就是做最小生成树的题，也就是Kruskal算法。

最小生成树的性质是最大边最小，那就先把所有边按照边权从小到大排序，然后挨个询问两端点是否连在一起。如果在一起就说明在树上了，否则将他们合并，记录一下sum++。这里的sum可以表示用来构建树的边，也可以表示在树上的节点数-1。总之当sum==节点数-1时就说明最小树已经构建完成，这时用过的边们是一种最小生成树的方案，最后一次加入的那个边的边权是这个图的最小生成树的最大边权。

比如洛谷上的这道题

要求每个村庄之间都能互相到达，说明至少要做一个树。又问最快什么时候通车，那就是最小生成树了。那么本题题意就是求最小生成树的最大边权，是一个模板题。用上面的策略可解。

using namespace std;
int i;
int m,n,sum;
int fa[1010];
struct lu
{
    int x,y;
    int t;
}o[100000];
bool Orz(lu a,lu b)
{
    return a.t<b.t;
}
int get(int x)
{
    if(x==fa[x])return x;        
    return fa[x]=get(fa[x]);
}
void hebing(int x,int y)
{
    x=get(x),y=get(y);
    fa[x]=y;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
//freopen("123.in","r",stdin);
//freopen("123.out","w",stdout);
    cin>>n>>m;
    for(i=1;i<=m;i++)
        cin>>o[i].x>>o[i].y>>o[i].t;
    sort(o+1,o+1+m,Orz);
    for(i=1;i<=n;i++)
        fa[i]=i;
    for(i=1;i<=m;i++)
        if(get(o[i].x)!=get(o[i].y))
        {
            hebing(o[i].x,o[i].y);
            sum++;
            if(sum==n-1)
            {
                cout<<o[i].t;
                return 0;
            }
        }
    cout<<-1;
}

最后分享一下从书中翻到的模板好了：

int fa[？];
int get(int x)
{
    if(x==fa[x])return x;        
    return fa[x]=get(fa[x]);//路径压缩
}
void hebing(int x,int y)
{
    fa[get(x)]=get(y);
}