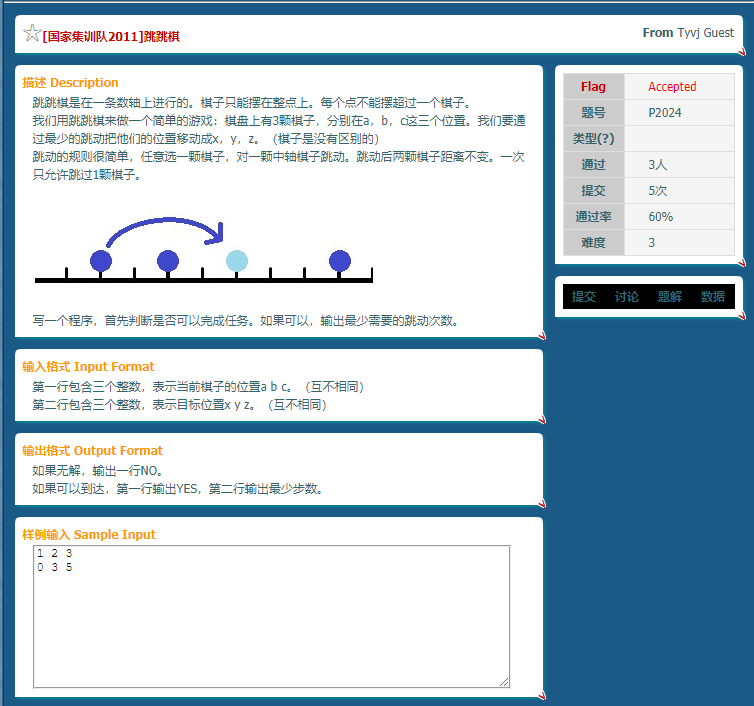
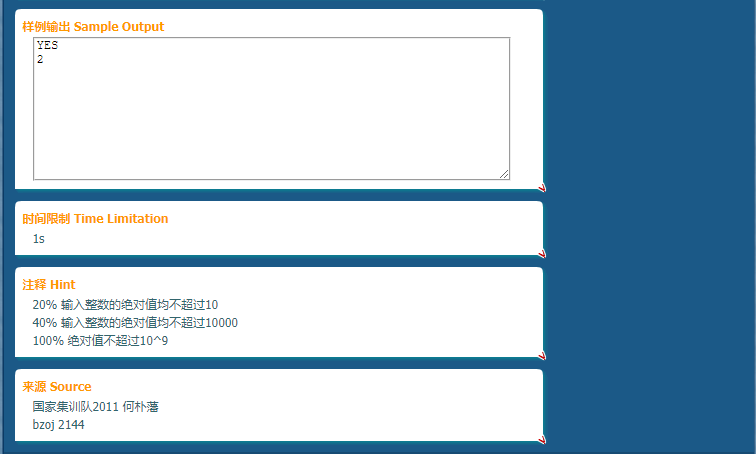
这是一道很有意思的题.不要被国家集训队的标签吓到,我们仔细思考跳的时候的性质.
玩过跳棋的应该都可以接受题意. 可以把每次'跳'分为两种:一种是中间的棋子以两边的棋子为'中轴棋子'跳,显然想向哪跳就向哪跳,只会跳过一个棋子.一种是两边的棋子向中间跳.这种可能不能跳:左中和中右间的距离相同,无法再跳.能跳也只会有一种情况:距离小一点的向距离更大的那两个棋子间跳.
画一下图应该比较容易理解.
比如样例1,2,3就只能向'外'跳了,1向2,3跳或 3向1,2跳就是不允许的.
比如样例0,3,5既能向'外'跳,5也能向'里'跳,0就不能向右跳.
也就是说,我们把所有的状态看做一个森林,根节点们一定都是x,y,z距离相同的状态.其他的所有状态存在且一定只存在与一棵树上面.
我们可以用这样的方法向上跳到一个状态的根节点上去:
每次算出xy,yz间的距离.令距离小的向距离大的点跳.直到距离相同.
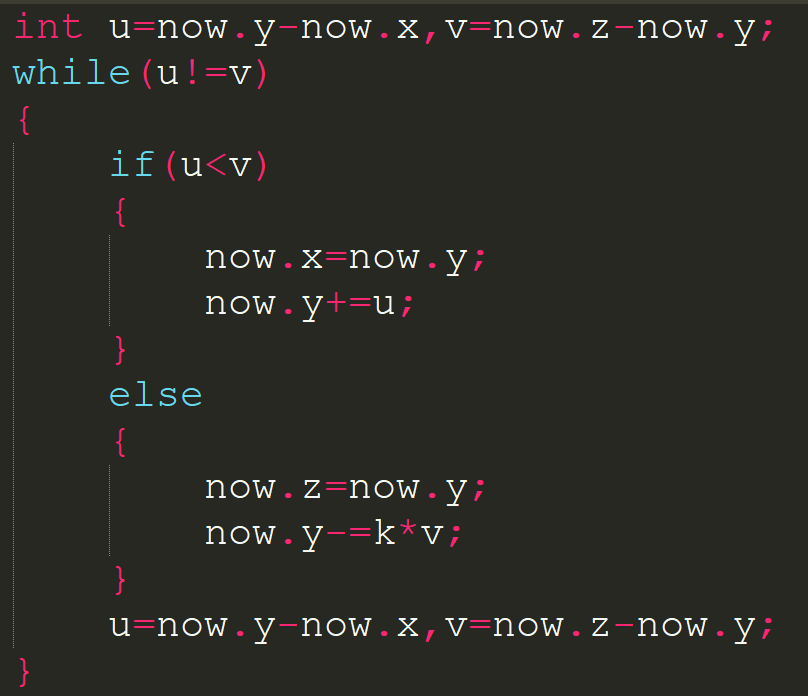
这样好像挺慢的对吧,如果y=x+1,我们需要跳z-y次.这个时候又发现好像可以连着跳...
例如如果u<v,我们可以连着跳上个v/u次.反之亦然.

这样就快了很多.从最坏2e9到最坏小于log(2e9).为什么会这样呢?不妨设u<v,跳完后总距离就会小于u,而u正是小于总距离的一半的.也就是说,每次跳k次后都会减少一半多.
基于这个while,我们还可以询问第k个祖先是谁,距离根节点的距离.于是仿照树上倍增LCA,本题就可以愉快的A掉了.我们先找到根节点,判断是否一样.然后调整到'深度'一样的,判断是否一样.然后向上调整.

using namespace std; struct node { long long x,y,z; long long deep; friend bool operator ==(node a,node b) { return a.x==b.x&&a.y==b.y&&a.z==b.z; } friend bool operator !=(node a,node b) { return !(a==b); } }a,b; void tiao(node &c) { if(c.x>c.y) swap(c.x,c.y); if(c.x>c.z) swap(c.x,c.z); if(c.y>c.z) swap(c.y,c.z); } node getfa(node now,long long s) { long long u=now.y-now.x,v=now.z-now.y; for(;s&&u!=v;) { if(u<v) { long long k=min((v-1)/u,s); now.x+=k*u;now.y+=k*u;s-=k; } else { long long k=min((u-1)/v,s); now.y-=k*v,now.z-=k*v,s-=k; } u=now.y-now.x,v=now.z-now.y; } return now; } long long getdeep(node now) { long long u=now.y-now.x,v=now.z-now.y,sum=0,k; for(;u!=v;) { if(u<v) { k=(v-1)/u; now.x+=k*u;now.y+=k*u; } else { k=(u-1)/v; now.y-=k*v,now.z-=k*v; } u=now.y-now.x,v=now.z-now.y; sum+=k; } return sum; } void write(node a) { cout<<a.x<<' '<<a.y<<' '<<a.z<<endl; } int main() { cin>>a.x>>a.y>>a.z>>b.x>>b.y>>b.z; tiao(a);tiao(b); if(getfa(a,2999999998)==getfa(b,2999999998)) { cout<<"YES"<<' '; } else { cout<<"NO"; return 0; } long long deep1=getdeep(a),deep2=getdeep(b); if(deep1>deep2) { a=getfa(a,deep1-deep2); } if(deep1<deep2) { b=getfa(b,deep2-deep1); } if(a==b) { cout<<abs(deep1-deep2); return 0; } long long sum=0; for(long long i=30;i>=0;i--) { node tx=getfa(a,1<<i),ty=getfa(b,1<<i); if(tx!=ty) { a=tx,b=ty; sum+=(1<<i); } } cout<<abs(deep1-deep2)+2*(sum+1); return 0; }
