splay是如何减少时间复杂度呢?让我先研读一下代码QAQ每次访问某个节点时都把它旋转到根节点.
以下转自https://blog.csdn.net/qq_31640513/article/details/76944892
共有三种情况.


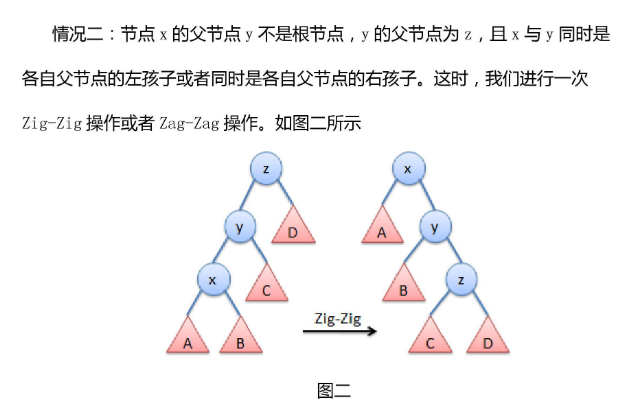
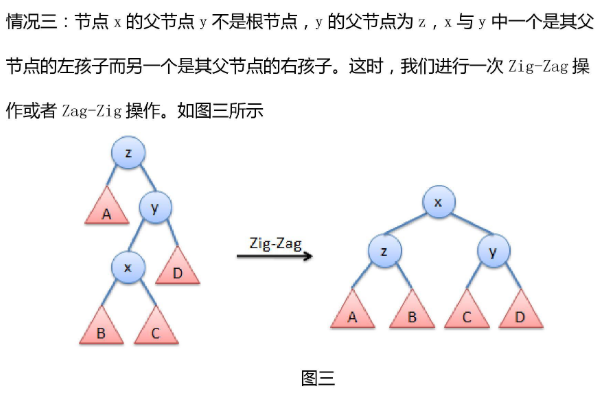
那不如直接上例题?(越来越懒)
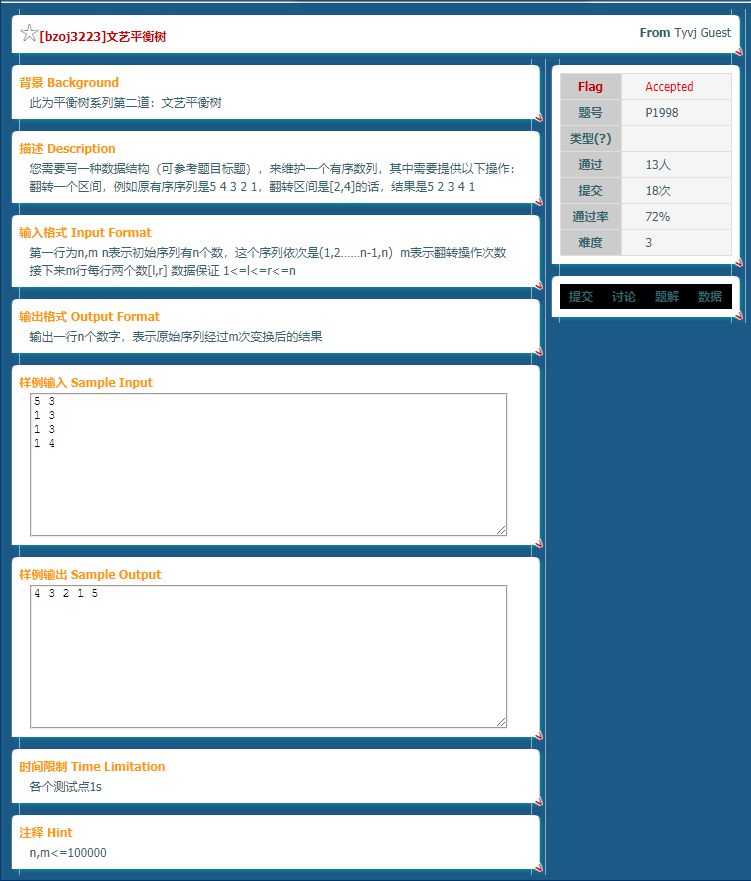
区间旋转怎么做啊??
我会splay,但是好像还不够,我还会打标记!
考虑每次区间旋转的时候,我们可以找到区间l的前驱,把他旋转到根节点,这样根节点和根节点的右子树是[1,l-1],左子树是[l,n],然后我们把r的后继旋转到根节点的右儿子,这样根节点的右儿子和右儿子的子树就是[l+1,n],根节点的右儿子的左子树即为区间[l,r],打标记走人!
输出就简单了,dfs(root),对于当前节点x,如果有标记就把标记下传并交换左右子树,然后dfs(左儿子),然后输出x,然后dfs(右儿子).
为什么复杂度能够保证呢?好像要用到势函数或摊还分析,告辞.
哦差点忘了放代码了.

#include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> using namespace std; #define INF 2000000007 char buf[1<<15],*fs,*ft; inline char getc(){ return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:* fs++; } inline int read(){ int This=0,F=1; char ch=getc(); while(ch<'0'||ch>'9'){ if(ch=='-') F=-1; ch=getc(); } while(ch>='0'&&ch<='9'){ This=(This<<1)+(This<<3)+ch-'0'; ch=getc(); } return This*F; } inline void write(int x) { if(x==0) { putchar('0'); putchar(32); return; } if(x<0) { putchar('-'); x=-x; } int num=0;char ch[16]; while(x) ch[++num]=x%10+'0',x/=10; while(num) putchar(ch[num--]); putchar(32); } struct node{ int l,r; int f,v,sz; bool flag; void set(int x) { v=x; //ch[0]=ch[1]=f=flag=0; sz=1; } }o[100010]; int n,m,root,tot,l,r,X1,X2; void updata(int x) { if(!x) return ; o[x].sz=1+o[o[x].l].sz+o[o[x].r].sz; } void PD(int x)//标记下传,旋转儿子 { if (!x) return ; if (o[x].flag) { o[o[x].l].flag^=1;o[o[x].r].flag^=1; o[x].flag=0; int t=o[x].l;o[x].l=o[x].r;o[x].r=t; } } void SC(int x,int y,bool z) { if(z) o[x].r=y; else o[x].l=y; o[y].f=x; } inline bool d(int x) {return o[o[x].f].r==x;} void rot(int x) { int y=o[x].f,z=o[y].f,tt=d(x); SC(z,x,d(y)); if(!tt) SC(y,o[x].r,tt); else SC(y,o[x].l,tt); SC(x,y,!tt); updata(y); } void splay(int x,int f) { PD(x); if (f==0) root=x; while (o[x].f!=f) { if (o[o[x].f].f==f) {rot(x);break;} if (d(x)==d(o[x].f)) {rot(o[x].f);rot(x);} else {rot(x);rot(x);} } updata(x); } int build(int l,int r) { if (l>r) return 0; tot++; int x=tot,mid=(l+r)>>1; o[x].set(mid); o[x].l=build(l,mid-1); o[x].r=build(mid+1,r); o[o[x].l].f=o[o[x].r].f=x; updata(x); return x; } int find(int x,int y) { PD(x); if (o[o[x].l].sz+1<y) return find(o[x].r,y-1-o[o[x].l].sz); else if (o[o[x].l].sz+1==y) return x; else return find(o[x].l,y); } void dfs(int x) { PD(x); if (o[x].l) dfs(o[x].l); write(o[x].v); if (o[x].r) dfs(o[x].r); } int main() { //freopen("123.in","r",stdin); n=read();m=read(); o[0].v=o[n+1].v=INF; root=build(0,n+1); while(m--) { l=read();r=read(); X1=find(root,l); X2=find(root,r+2); splay(X1,0); splay(X2,X1); updata(root); o[o[X2].l].flag^=1; updata(o[X2].l);updata(X2);updata(root); } dfs(root); return 0; }
