p1250

　　先吹一波程序跑的速度

　　

　　然后来看题:

　　

　　

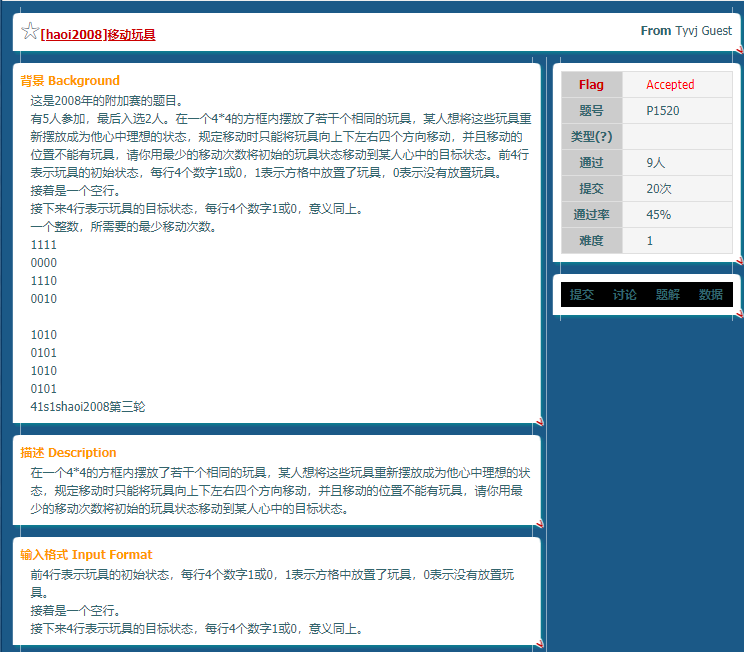
　　给出两个4*4的棋盘状态,问你最少移动多少步使得一个状态转移到另一个状态.只能向上下左右移动,移动的位置不能有其他棋子.

　　刚开始认为很贪心,但是显然不是.然后考虑才16个棋子不如把所有状态都列一下2^16才65236个状态更何况达不到这么多.大概是多少呢?应该是2^8=256吧 我猜的.然后考虑怎么写和怎么优化.首先那句"不能有其他棋子"是没啥用的,想把一个棋子移动到另一个地方需要的步数与中间是否有棋子无关.把它想象成一个个空的话想用这个棋子天上那个空的步数一定是abs(x1-x2)+abs(y1-y2).也就是说我可以把所有的两个棋盘上同一位置都有的棋子视为没有,最复杂的时候是8个.考虑如何转移呢?好像可以用二进制表示啥的,但是我觉得有点麻烦啊.

　　这里介绍一种新的方法:直接dfs判断.就相当于一个二分图匹配,左边sum个棋子与右边sum个棋子需要匹配,匹配的代价都可以算出来,sum<=8,显然是可以直接dfs的啊.比如样例:

　　先扔掉没用的点:

　　

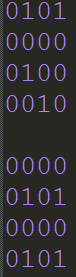
　　二分图:左边图一,右边图二

　　

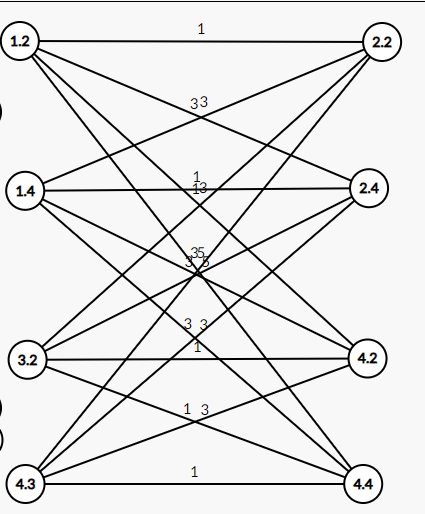
　　然后就可以开开心心的dfs了,稳定的n^n,n<=8;

　

using namespace std;
int i,f;
int d[10][10],sum,sum1,sum2,ans=1000000;
char t,map[5][5];
struct node{
    int x,y;
}o1[10],o2[10];
void dfs(int deep,int now){
    /*if(now>=ans)
        return ;*/
    if(deep==sum+1){    
        ans=min(ans,now);
        return ;
    }
    for(int j=1;j<=sum;j++){
        if(flag[j])continue;
        flag[j]=1;
        dfs(deep+1,now+d[deep][j]);
        flag[j]=0;
    }
    return ;
}
int main(){ 
    for(i=1;i<=4;i++)
        for(f=1;f<=4;f++)
            cin>>map[i][f];
    for(i=1;i<=4;i++)
        for(f=1;f<=4;f++){
            cin>>t;
            if(t!=map[i][f]){
                if(t=='0'){
                    sum1++;
                    o1[sum1].x=i;
                    o1[sum1].y=f;
                }
                else{
                    sum2++;
                    o2[sum2].x=i;
                    o2[sum2].y=f;
                }
            }
        }
    for(i=1;i<=sum1;i++)
        for(f=1;f<=sum1;f++)
            d[i][f]=abs(o1[i].x-o2[f].x)+abs(o1[i].y-o2[f].y);
    sum=sum1;
    dfs(1,0);
    cout<<ans;
    return 0;
}