纹理分析是对图像灰度(浓淡)空间分布模式的提取和分析。纹理分析在遥感图像、X射线照片、细胞图像判读和处理方面有广泛的应用。关于纹理,还没有一个统一的数学模型。它起源于表征纺织品表面性质的纹理概念,可以用来描述任何物质组成成分的排列情况,例如医学上X 射线照片中的肺纹理、血管纹理、航天(或航空)地形照片中的岩性纹理等。图像处理中的视觉纹理通常理解为某种基本模式(色调基元)的重复排列。因此描述一种纹理包括确定组成纹理的色调基元和确定色调基元间的相互关系。纹理是一种区域特性,因此与区域的大小和形状有关。两种纹理模式之间的边界,可以通过观察纹理度量是否发生显著改变来确定。纹理是物体结构的反映,分析纹理可以得到图像中物体的重要信息,是图像分割、特征抽取和分类识别的重要手段。对于空间域图像或变换域图像(见图像变换),可以用统计和结构两种方法进行纹理分析。
统计纹理分析寻找刻划纹理的数字特征,用这些特征或同时结合其他非纹理特征对图像中的区域(而不是单个像素)进行分类。图像局部区域的自相关函数、灰度共生矩阵、灰度游程以及灰度分布的各种统计量,是常用的数字纹理特征。如灰度共生矩阵用灰度的空间分布表征纹理。由于粗纹理的灰度分布随距离的变化比细纹理缓慢得多,因此二者有完全不同的灰度共生矩阵。
结构纹理分析研究组成纹理的基元和它们的排列规则。基元可以是一个像素的灰度、也可以是具有特定性质的连通的像素集合。基元的排列规则常用树文法来描述。
英文名称 Texture Analysis;
学术解释
指通过一定的图像处理技术提取出纹理特征参数,从而获得纹理的定量或定性描述的处理过程.纹理分析方法按其性质而言,可分为两大类:统计分析方法和结构分析方法
学术定义
纹理是一种普遍存在的视觉现象,目前对于纹理的精确定义还未形成统一认识,多根据应用需要做出不同定义.
定义1 按一定规则对元素(elements)或基元(primitives)进行排列所形成的重复模式.
定义2 如果图像函数的一组局部属性是恒定的,或者是缓变的,或者是近似周期性的,则图象中的对应区域具有恒定的纹理.
作用分析
对这种表面纹理的研究称为纹理分析.它在计算机视觉领域有着重要的应用.
在机械工程中对机械零件加工表面的这种凹凸不平性开展研究同样具有重要的实践意义。
对图像灰度空间分布模式提取和分析
纹理分析在遥感图像、 X射线照片、细胞图像判读和处理方面有广泛的应用。关于纹理,还没有一个统一的数学模型。它起源于表征纺织品表面性质的纹理概念,可以用来描述任何物质组成成分的排列情况,例如医学上X 射线照片中的肺纹理、血管纹理、航天(或航空)地形照片中的岩性纹理等。图像处理中的视觉纹理通常理解为某种基本模式(色调基元)的重复排列。因此描述一种纹理包括确定组成纹理的色调基元和确定色调基元间的相互关系。纹理是一种区域特性,因此与区域的大小和形状有关。两种纹理模式之间的边界,可以通过观察纹理度量是否发生显著改变来确定。纹理是物体结构的反映,分析纹理可以得到图像中物体的重要信息,是图像分割、特征抽取和分类识别的重要手段。对于空间域图像或变换域图像(见图像变换),可以用
统计和结构两种方法进行纹理分析
统计纹理分析寻找刻划纹理的数字特征,用这些特征或同时结合其他非纹理特征对图像中的区域(而不是单个像素)进行分类。图像局部区域的自相关函数、灰度共生矩阵、灰度游程以及灰度分布的各种统计量,是常用的数字纹理特征。如灰度共生矩阵用灰度的空间分布表征纹理。由于粗纹理的灰度分布随距离的变化比细纹理缓慢得多,因此二者有完全不同的灰度共生矩阵。
结构纹理分析研究组成纹理的基元和它们的排列规则。基元可以是一个像素的灰度、也可以是具有特定性质的连通的像素集合。基元的排列规则常用树文法来描述。
纹理基元与影调
一个纹理基元(不严格地说)是一个具有一定的不变特性的视觉基元。这些不变特性在给定区域内的不同位置上,以不同的变形和不同的方向重复出现。纹理基元最基本的不变特性之一是区域内象素的灰度分布,而影调也是表示灰度的明暗分布。
因此,我们认为影调和纹理不是独立的概念:当在图象的一定面积区域中影调基元的变化很小时,这个区域的主导特性是影调。当在小面积区域中含大量不同的影调,这个区域占主导的特性是纹理。
spatial gray level co-occurrence matrix 空间灰度共生矩阵(GLCM)
spatial gray level dependence matrix 空间灰度相关矩阵
spatial gray-level dependence matrices 空间灰度独立矩阵
Texture
纹理特征建立在子对象基础之上,这就意味着,必须有一个对象等级架构去使用他们,精确的分割是使用形状纹理特征的基础,子对象的分割要尽量有意义
1.考虑子对象光谱特征的纹理
2.考虑子对象形状特征的纹理
3.基于灰度共生矩阵的纹理
1.Layer Value Texture Based on Subobjects
—【Mean of sub-objects: stddev】子对象均值标准差,对象分割的子对象更隔阂,则该特征更有意义;
—【Avrg. mean diff. to neighbors of subobjects】通过一个对象内部子对象在某一个图层(k)上与邻域(d)对象的差异取平均来进行对比,反应该对象内部差异的平均值。
2.Shape Texture Based on Subobjects
—【Area of subobjects: mean】所包含子对象的平均面积;
—【Area of subobjects: stddev.】所包含子对象的面积的标准差;
—【Density of subobjects: mean 】子对象密度平均值(参考对象形状特征中的Density );
—【Density of subobjects: stddev. 】子对象密度的标准差;
—【Asymmetry of subobjects: mean 】子对象不对称性的平均值;
—【Asymmetry of subobjects: stddev. 】子对象不对称性的标准差;
—【Direction of subobjects: mean 】方向权重是相关子对象的的不对称性,越不对称,对主方向的影响越大,算法首先比较所有子对象主方向在90-180之间的做(direction-180),即顺是真旋转180度,然后计算等级距离d下的所有子对象的主方向(权重)均值;
—【Direction of subobjects: stddev. 】子对象主方向的标准差。
3.Texture After Haralick P.152
灰度共生矩阵(http://blog.csdn.net/Redeom/archive/2008/04/17/2301823.aspx)
共生矩阵用两个位置的象素的联合概率密度来定义,它不仅反映亮度的分布特性,也反映具有同样亮度或接近亮度的象素之间的位置分布特性,是有关图象亮度变化的二阶统计特征。它是定义一组纹理特征的基础。
一幅图象的灰度共生矩阵能反映出图象灰度关于方向、相邻间隔、变化幅度的综合信息,它是分析图象的局部模式和它们排列规则的基础。
设f(x,y)为一幅二维数字图象,其大小为M×N,灰度级别为Ng,则满足一定空间关系的灰度共生矩阵为
P(i,j)=#{(x1,y1),(x2,y2)∈M×N|f(x1,y1)=i,f(x2,y2)=j}
其中#(x)表示集合x中的元素个数,显然P为Ng×Ng的矩阵,若(x1,y1)与(x2,y2)间距离为d,两者与坐标横轴的夹角为θ,则可以得到各种间距及角度的灰度共生矩阵P(i,j,d,θ)。
共生矩阵的一个计算例子见下图,其中(a)为原始图像的灰度值,(b)为从左到右方向上的共生矩阵,θ=0,(c)为从左下到右上方向上的共生矩阵,θ=45,(d)为从下到上方向共生矩阵,θ=90,(e)为从右下到左上方向上的共生矩阵,θ=135,相邻间隔d=1。
纹理特征提取的一种有效方法是以灰度级的空间相关矩阵即共生矩阵为基础的,因为图像中相距(Δx,Δy)的两个灰度像素同时出现的联合频率分布可以用灰度共生矩阵来表示。若将图像的灰度级定为N级,那么共生矩阵为N×N矩阵,可表示为M(Δx,Δy)(h,k),其中位于(h,k)的元素mhk的值表示一个灰度为h而另一个灰度为k的两个相距为(Δx,Δy)的像素对出现的次数。
对粗纹理的区域,其灰度共生矩阵的mhk值较集中于主对角线附近。因为对于粗纹理,像素对趋于具有相同的灰度。而对于细纹理的区域,其灰度共生矩阵中的mhk值则散布在各处。
为了能更直观地以共生矩阵描述纹理状况,从共生矩阵导出一些反映矩阵状况的参数,典型的有以下几种:
(1)能量:是灰度共生矩阵元素值的平方和,所以也称能量,反映了图像灰度分布均匀程度和纹理粗细度。如果共生矩阵的所有值均相等,则ASM值小;相反,如果其中一些值大而其它值小,则ASM值大。当共生矩阵中元素集中分布时,此时ASM值大。ASM值大表明一种较均一和规则变化的纹理模式。
(2)对比度:反映了图像的清晰度和纹理沟纹深浅的程度。纹理沟纹越深,其对比度越大,视觉效果越清晰;反之,对比度小,则沟纹浅,效果模糊。灰度差即对比度大的象素对越多,这个值越大。灰度公生矩阵中远离对角线的元素值越大,CON越大。
(3)相关:它度量空间灰度共生矩阵元素在行或列方向上的相似程度,因此,相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时,相关值就大;相反,如果矩阵像元值相差很大则相关值小。如果图像中有水平方向纹理,则水平方向矩阵的COR大于其余矩阵的COR值。
(4)熵:是图像所具有的信息量的度量,纹理信息也属于图像的信息,是一个随机性的度量,当共生矩阵中所有元素有最大的随机性、空间共生矩阵中所有值几乎相等时,共生矩阵中元素分散分布时,熵较大。它表示了图像中纹理的非均匀程度或复杂程度。
(5)逆差距:反映图像纹理的同质性,度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化,局部非常均匀。
其它参数:中值<Mean>、协方差<Variance>、同质性/逆差距<Homogeneity>、反差 <Contrast>、差异性<Dissimilarity>、熵<Entropy>、二阶距< Angular Second Moment>、自相关<Correlation>
参考文献:高分辨率卫星影像中阴影的自动提取与处理,许妙忠余志惠。
http://apps.hi.baidu.com/share/detail/37069002
共生矩阵用两个位置的象素的联合概率密度来定义,它不仅反映亮度的分布特性,也反映具有同样亮度或接近亮度的象素之间的位置分布特性,是有关图象亮度变化的二阶统计特征。它是定义一组纹理特征的基础。
一幅图象的灰度共生矩阵能反映出图象灰度关于方向、相邻间隔、变化幅度的综合信息,它是分析图象的局部模式和它们排列规则的基础。
设f(x,y)为一幅二维数字图象,其大小为M×N,灰度级别为Ng,则满足一定空间关系的灰度共生矩阵为
P(i,j)=#{(x1,y1),(x2,y2)∈M×N|f(x1,y1)=i,f(x2,y2)=j}
其中#(x)表示集合x中的元素个数,显然P为Ng×Ng的矩阵,若(x1,y1)与(x2,y2)间距离为d,两者与坐标横轴的夹角为θ,则可以得到各种间距及角度的灰度共生矩阵P(i,j,d,θ)。
纹理特征提取的一种有效方法是以灰度级的空间相关矩阵即共生矩阵为基础的[7],因为图像中相距(Δx,Δy)的两个灰度像素同时出现的联合频率分布可以用灰度共生矩阵来表示。若将图像的灰度级定为N级,那么共生矩阵为N×N矩阵,可表示为M(Δx,Δy)(h,k),其中位于(h,k)的元素mhk的值表示一个灰度为h而另一个灰度为k的两个相距为(Δx,Δy)的像素对出现的次数。
对粗纹理的区域,其灰度共生矩阵的mhk值较集中于主对角线附近。因为对于粗纹理,像素对趋于具有相同的灰度。而对于细纹理的区域,其灰度共生矩阵中的mhk值则散布在各处。
为了能更直观地以共生矩阵描述纹理状况,从共生矩阵导出一些反映矩阵状况的参数,典型的有以下几种:
(1)能量:是灰度共生矩阵元素值的平方和,所以也称能量,反映了图像灰度分布均匀程度和纹理粗细度。如果共生矩阵的所有值均相等,则ASM值小;相反,如果其中一些值大而其它值小,则ASM值大。当共生矩阵中元素集中分布时,此时ASM值大。ASM值大表明一种较均一和规则变化的纹理模式。
(2)对比度:,其中。反映了图像的清晰度和纹理沟纹深浅的程度。纹理沟纹越深,其对比度越大,视觉效果越清晰;反之,对比度小,则沟纹浅,效果模糊。灰度差即对比度大的象素对越多,这个值越大。灰度公生矩阵中远离对角线的元素值越大,CON越大。
(3)相关:它度量空间灰度共生矩阵元素在行或列方向上的相似程度,因此,相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时,相关值就大;相反,如果矩阵像元值相差很大则相关值小。如果图像中有水平方向纹理,则水平方向矩阵的COR大于其余矩阵的COR值。
(4)熵:是图像所具有的信息量的度量,纹理信息也属于图像的信息,是一个随机性的度量,当共生矩阵中所有元素有最大的随机性、空间共生矩阵中所有值几乎相等时,共生矩阵中元素分散分布时,熵较大。它表示了图像中纹理的非均匀程度或复杂程度。
(5)逆差距:反映图像纹理的同质性,度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化,局部非常均匀。
其它参数:
中值<Mean>
协方差<Variance>
同质性/逆差距<Homogeneity>
反差<Contrast>
差异性<Dissimilarity>
熵<Entropy>
二阶距<Angular Second Moment>
自相关<Correlation>
当图像的局部有较小的方差时,则灰度值占有支配地位,当图像的局部有较大的方差时,则纹理占有支配地位。纹理是和局部灰度及其空间组织相联系的,纹理在识别感兴趣的目标和地区中有着非常重要的作用。
灰度共生矩阵表示了灰度的空间依赖性,它表示了在一种纹理模式下的像素灰度的空间关系。它的弱点是没有完全抓住局部灰度的图形特点,因此对于较大的局部,此方法的效果不太理想。灰度共生矩阵为方阵,维数等于图像的灰度级。灰度共生矩阵中的元素(i,j)的值表示了在图像中其中一个像素的灰度值为i,另一个像素的灰度值为j,并且相邻距离为d,方向为A的这样两个像素出现的次数。在实际应用中A一般选择为0°、45°、90°、135°。一般来说灰度图像的灰度级为256,在计算由灰度共生矩阵推导出的纹理特征时,要求图像的灰度级远小于256,主要是因为矩阵维数较大而窗口的尺寸较小则灰度共生矩阵不能很好表示纹理,如要能够很好表示纹理则要求窗口尺寸较大,这样使计算量大大增加,而且当窗口尺寸较大时对于每类的边界区域误识率较大。所以在计算灰度共生矩阵之前需要对图像进行直方图规定化,以减小图像的灰度级,一般规定化后的图像的灰度级为8或16。由灰度共生矩阵能够导出许多纹理特征,本文计算了14种灰度共生矩阵特征,分别为纹理二阶距、纹理熵、纹理对比度、纹理均匀性、纹理相关、逆差分矩、最大概率、纹理方差、共生和均值、共生和方差、共生和熵、共生差均值、共生差方差、共生差熵。
由灰度共生矩阵能够导出许多纹理特征,计算了14种灰度共生矩阵特征,分别为纹理二阶距、纹理熵、纹理对比度、纹理均匀性、纹理相关、逆差分矩、最大概率、纹理方差、共生和均值、共生和方差、共生和熵、共生差均值、共生差方差、共生差熵。
目前,人们对遥感影像上的纹理特征的含义理解不尽相同,纹理有时被称为结构、影纹和纹形等。Pickett认为纹理为保持一定的特征重复性并且间隔规律可以任意安排的空间结构。HawKins认为[6]纹理具有三大标志:某种局部序列性不断重复、非随机排列和纹理区域内大致为均匀的统一体。LiWang和D. C. He认为[7],纹理是纹理基元组成的,纹理基元被认为是表现纹理特征的最小单元,是一个像元在
其周围8个方向上的特征反应。纹理特征有时是明显的,以某种基本图形在某一地区有规律的周期性出现,例如:大面积森林覆盖地区的影像构成的纹理为斑点状,沙漠地区的影像构成的纹理为链状、新月状等;而有时纹理特征是不明显的、隐晦的,具有不稳定性。一般来说,前者纹理比较均一,后者纹理比较复杂[9]。
纹理作为一种区域特征,是对于图像各像元之间空间分布的一种描述。由于纹理能充分利用图像信息,无论从理论上或常识出发它都可以成为描述与识别图像的重要依据,与其他图像特征相比,它能更好地兼顾图像宏观性质与细微结构两个方面,因此纹理成为目标识别需要提取的重要特征。提取纹理特征的方法很多,如基于局部统计特性的特征、基于随机场模型的特征、基于空间频率的特征、分形特征等,其中,应用最广泛的是基于灰值共生矩阵的特征[10]。
%************************************************************************** % 图像检索——纹理特征 %基于共生矩阵纹理特征提取,d=1,θ=0°,45°,90°,135°共四个矩阵 %所用图像灰度级均为256 %参考《基于颜色空间和纹理特征的图像检索》 %function : T=Texture(Image) %Image : 输入图像数据 %T : 返回八维纹理特征行向量 %************************************************************************** function T = Texture(path) Image = imread(path); % [M,N,O] = size(Image); M = 256; N = 256; if isrgb(Image)%判断是否是RGB Gray=rgb2gray(Image); end %————————————————————————– %1.将各颜色分量转化为灰度 %————————————————————————– %Gray = double(0.3*Image(:,:,1)+0.59*Image(:,:,2)+0.11*Image(:,:,3)) %————————————————————————– %2.为了减少计算量,对原始图像灰度级压缩,将Gray量化成16级 %————————————————————————– for i = 1:M for j = 1:N for n = 1:256/16 if (n-1)*16<=Gray(i,j)&Gray(i,j)<=(n-1)*16+15 Gray(i,j) = n-1; end end end end %-------------------------------------------------------------------------- %3.计算四个共生矩阵P,取距离为1,角度分别为0,45,90,135 %-------------------------------------------------------------------------- P = zeros(16,16,4); for m = 1:16 for n = 1:16 for i = 1:M for j = 1:N if j P(m,n,1) = P(m,n,1)+1; P(n,m,1) = P(m,n,1); end if i>1&j P(m,n,2) = P(m,n,2)+1; P(n,m,2) = P(m,n,2); end if i P(m,n,3) = P(m,n,3)+1; P(n,m,3) = P(m,n,3); end if i P(m,n,4) = P(m,n,4)+1; P(n,m,4) = P(m,n,4); end end end if m==n P(m,n,:) = P(m,n,:)*2; end end end %%--------------------------------------------------------- % 对共生矩阵归一化 %%--------------------------------------------------------- for n = 1:4 P(:,:,n) = P(:,:,n)/sum(sum(P(:,:,n))); end %-------------------------------------------------------------------------- %4.对共生矩阵计算能量、熵、惯性矩、相关4个纹理参数 %-------------------------------------------------------------------------- H = zeros(1,4); I = H; Ux = H; Uy = H; deltaX= H; deltaY = H; C =H; for n = 1:4 E(n) = sum(sum(P(:,:,n).^2)); %%能量 for i = 1:16 for j = 1:16 if P(i,j,n)~=0 H(n) = -P(i,j,n)*log(P(i,j,n))+H(n); %%熵 end I(n) = (i-j)^2*P(i,j,n)+I(n); %%惯性矩 Ux(n) = i*P(i,j,n)+Ux(n); %相关性中μx Uy(n) = j*P(i,j,n)+Uy(n); %相关性中μy end end end for n = 1:4 for i = 1:16 for j = 1:16 deltaX(n) = (i-Ux(n))^2*P(i,j,n)+deltaX(n); %相关性中σx deltaY(n) = (j-Uy(n))^2*P(i,j,n)+deltaY(n); %相关性中σy C(n) = i*j*P(i,j,n)+C(n); end end C(n) = (C(n)-Ux(n)*Uy(n))/deltaX(n)/deltaY(n); %相关性 end %-------------------------------------------------------------------------- %求能量、熵、惯性矩、相关的均值和标准差作为最终8维纹理特征 %-------------------------------------------------------------------------- T(1) = mean(E); T(2) = sqrt(cov(E)); T(3) = mean(H); T(4) = sqrt(cov(H)); T(5) = mean(I); T(6) = sqrt(cov(I)); T(7) = mean(C); T(8) = sqrt(cov(C));
在计算灰度共生矩阵前,需要做影像的量化比如将256级影像量化为128级。有一种方法是线性量化,但是这种方法有可能对原始影像的纹理产生人为地影响,太“粗了”。所以想请教大家是否还有其他较好的影像灰度级量化的方法?
http://blog.csdn.net/linxue968/article/details/6034745
图像的灰度共生矩阵GLCM(matlab 函数帮助)
Gray-level co-occurrence matrix from an image
图像的灰度共生矩阵
灰度共生矩阵是像素距离和角度的矩阵函数,它通过计算图像中一定距离和一定方向的两点灰度之间的相关性,来反映图像在方向、间隔、变化幅度及快慢上的综合信息。
使用方法:
glcm = graycomatrix(I)
glcms = graycomatrix(I,param1,val1,param2,val2,...)
[glcms,SI] = graycomatrix(...)
描述:
glcms = graycomatrix(I) 产生图像I的灰度共生矩阵GLCM。它是通过计算两灰度值在图像I中水平相邻的次数而得到的 (也不必是水平相邻的次数,这一参数是可调的,可能通过Offsets来进行调整,比如[0 D]代表是水平方向,[-D D]代表是右上角45度方向,[-D 0]代表是竖直方向,即90度方向,而[-D -D]则代表是左上角,即135度方向),GLCM中的每一个元素(i,j)代表灰度i与灰度j在图像中水平相邻的次数。
因为动态地求取图像的GLCM区间代价过高,我们便首先将灰度值转换到I的灰度区间里。如果I是一个二值图像,那么灰度共生矩阵就将图像转换到两级。如果I是一个灰度图像,那将转换到8级。灰度的级数决定了GLCM的大小尺寸。你可以通过设定参数“NumLevels”来指定灰度的级数,还可以通过设置“GrayLimits"参数来设置灰度共生矩阵的转换方式。
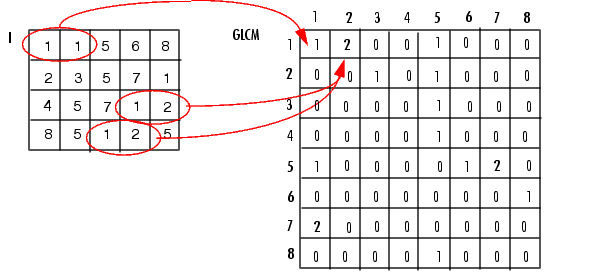
下图显示了如何求解灰度共生矩阵,以(1,1)点为例,GLCM(1,1)值为1说明只有一对灰度为1的像素水平相邻。GLCM(1,2)值为2,是因为有两对灰度为1和2的像素水平相邻。
glcms = graycomatrix(I,param1,val1,param2,val2,...) 返回一个或多个灰度灰度共生矩阵,根据指定的参数。参数可以很简短,并且对大小写不敏感。
参数
'GrayLimits' 是两个元素的向量,表示图像中的灰度映射的范围,如果其设为[],灰度共生矩阵将使用图像I的最小及最大灰度值作为GrayLimits
'NumLevels' 一个整数,代表是将图像中的灰度归一范围。举例来说,如果NumLevels为8,意思就是将图像I的灰度映射到1到8之间,它也决定了灰度共生矩阵的大小
'Offset' 上面有解释,是一个p*2的整数矩阵,D代表是当前像素与邻居的距离,通过设置D值,即可设置角度
Angle Offset
0 [0 D]
45 [-D D]
90 [-D 0]
135 [-D -D]
示例:
计算灰度共生矩阵,并且返回缩放后的图像,SI
I = [ 1 1 5 6 8 8; 2 3 5 7 0 2; 0 2 3 5 6 7];
[glcm,SI] = graycomatrix(I,'NumLevels',9,'G',[])
计算灰度图像的灰度共生矩阵
I = imread('circuit.tif');
glcm = graycomatrix(I,'Offset',[2 0]);
灰度共生矩阵的特征:
角二阶矩(Angular Second Moment, ASM)
ASM=sum(p(i,j).^2) p(i,j)指归一后的灰度共生矩阵
角二阶矩是图像灰度分布均匀程度和纹理粗细的一个度量,当图像纹理绞细致、灰度分布均匀时,能量值较大,反之,较小。
熵(Entropy, ENT)
ENT=sum(p(i,j)*(-ln(p(i,j)))
是描述图像具有的信息量的度量,表明图像的复杂程序,当复杂程序高时,熵值较大,反之则较小。
反差分矩阵(Inverse Differential Moment, IDM)
IDM=sum(p(i,j)/(1+(i-j)^2))
反映了纹理的清晰程度和规则程度,纹理清晰、规律性较强、易于描述的,值较大;杂乱无章的,难于描述的,值较小
灰度共生矩阵就是一种通过研究灰度的空间相关特性来描述纹理的常用方法。
灰度共生矩阵是对图像上保持某距离的两象素分别具有某灰度的状况进行统计得到的。
取图像(N×N)中任意一点(x,y)及偏离它的另一点(x+a,y+b),设该点对的灰度值为(g1,g2)。令点(x,y)在整个画面上移动,则会得到各种(g1,g2)。值,设灰度值的级数为,则(g1,g2)。的组合共有 k2种。对于整个画面,统计出每一种(g1,g2)值出现的次数,然后排列成一个方阵,在用(g1,g2)出现的总次数将它们归一化为出现的概率P(g1,g2),这样的方阵称为灰度共生矩阵。距离差分值(a,b)取不同的数值组合,可以得到不同情况下的联合概率矩阵。(a,b)取值要根据纹理周期分布的特性来选择,对于较细的纹理,选取(1,0)、(1,1)、(2,0)等小的差分值。
为了能更直观地以共生矩阵描述纹理状况,从共生矩阵导出一些反映矩阵状况的参数,典型的有以下几种:
(1)能量:是灰度共生矩阵元素值的平方和,所以也称能量,反映了图像灰度分布均匀程度和纹理粗细度。如果共生矩阵的所有值均相等,则ASM值小;相反, 如果其中一些值大而其它值小,则ASM值大。当共生矩阵中元素集中分布时,此时ASM值大。ASM值大表明一种较均一和规则变化的纹理模式。
(2)对比度:反映了图像的清晰度和纹理沟纹深浅的程度。纹理沟纹越深,其对比度越大,视觉效果越清晰;反之,对比度小,则沟纹浅,效果模糊。灰度差即对比度大的象素对越多,这个值越大。灰度公生矩阵中远离对角线的元素值越大,CON越大。
(3)相关:它度量空间灰度共生矩阵元素在行或列方向上的相似程度,因此,相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时,相关值就大; 相反,如果矩阵像元值相差很大则相关值小。如果图像中有水平方向纹理,则水平方向矩阵的COR大于其余矩阵的COR值。
(4)熵:是图像所具有的信息量的度量,纹理信息也属于图像的信息,是一个随机性的度量,当共生矩阵中所有元素有最大的随机性、空间共生矩阵中所有值几乎相等时,共生矩阵中元素分散分布时,熵较大。它表示了图像中纹理的非均匀程度或复杂程度。
(5)逆差距: 反映图像纹理的同质性,度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化,局部非常均匀。
其它参数:中值<Mean>、协方差<Variance>、同质性/逆差距<Homogeneity>、反差<Contrast>、差异性<Dissimilarity>、熵<Entropy>、二阶距< Angular Second Moment>、自相关<Correlation>
image=imread('F:/1021-4.bmp');
%计算图像的灰度共生矩阵
[glcms,SI]=graycomatrix(image);
%计算图像的灰度共生矩阵
stats = graycoprops(glcms,'Contrast Correlation energy')
%灰度共生矩阵纹理特征提取
%提取了三个特征参数。f1为角二阶矩,f2为相关度,f3为熵
clc
clear
tu=imread('nvxing19.jpg');
IN=rgb2gray(tu); %灰度化
g=256;
[R,C]=size(IN);
p1=zeros(g); %计算共生矩阵
for M=1:R
for N=1:(C-1)
p1(IN(M,N)+1,IN(M,N+1)+1)= p1(IN(M,N)+1,IN(M,N+1)+1)+1;
p1(IN(M,N+1)+1,IN(M,N)+1)= p1(IN(M,N+1)+1,IN(M,N)+1)+1;
end
end
p2=double(p1)/(M*N); %归一化
%计算角二阶矩 f1
f1=p2.^2;
f1=sum(f1(:))
% 计算相关度 f2
colour=0:(g-1);
m1=sum(p2)*colour(:);
m2=m1;
pp=sum(p2);
v1=((colour-m1).^2)*pp(:);
v2=v1;
[m,n]=meshgrid(colour,colour);
pp=m.*n.*p2;
f2=(sum(pp(:))-m1*m2)/(v1+eps)*(v2+eps)
%计算墒 f3
pp=(p2.*log2(p2+eps));
f3=-sum(pp(:));
%计算对比度 f4
f4=0;
k_f4=0;
for k=1:g-1
for i=1:g-1
if(i+k)<=g
k_f4=k_f4+2*p2(i,i+k);
end
end
f4=f4+k_f4*k^2;
end
%计算逆矩阵 f5
f5=0;
for k=1:g
for j=1:g
f5=f5+p2(k,j)/(1+(j-k)^2);
end
end
Matlab中实现灰度共生矩阵
%**************************************************************************
% 图像检索——纹理特征
%基于共生矩阵纹理特征提取,d=1,θ=0°,45°,90°,135°共四个矩阵
%所用图像灰度级均为256
%参考《基于颜色空间和纹理特征的图像检索》
%function : T=Texture(Image)
%Image : 输入图像数据
%T : 返回八维纹理特征行向量
%**************************************************************************
% function T = Texture(Image)
Gray = imread('d:
esult5.bmp');
[M,N,O] = size(Gray);
M = 128;
N = 128;
%--------------------------------------------------------------------------
%1.将各颜色分量转化为灰度
%--------------------------------------------------------------------------
% Gray = double(0.3*Image(:,:,1)+0.59*Image(:,:,2)+0.11*Image(:,:,3));
%--------------------------------------------------------------------------
%2.为了减少计算量,对原始图像灰度级压缩,将Gray量化成16级
%--------------------------------------------------------------------------
for i = 1:M
for j = 1:N
for n = 1:256/16
if (n-1)*16<=Gray(i,j)&Gray(i,j)<=(n-1)*16+15
Gray(i,j) = n-1;
end
end
end
end
%--------------------------------------------------------------------------
%3.计算四个共生矩阵P,取距离为1,角度分别为0,45,90,135
%--------------------------------------------------------------------------
P = zeros(16,16,4);
for m = 1:16
for n = 1:16
for i = 1:M
for j = 1:N
if j<N&Gray(i,j)==m-1&Gray(i,j+1)==n-1
P(m,n,1) = P(m,n,1)+1;
P(n,m,1) = P(m,n,1);
end
if i>1&j<N&Gray(i,j)==m-1&Gray(i-1,j+1)==n-1
P(m,n,2) = P(m,n,2)+1;
P(n,m,2) = P(m,n,2);
end
if i<M&Gray(i,j)==m-1&Gray(i+1,j)==n-1
P(m,n,3) = P(m,n,3)+1;
P(n,m,3) = P(m,n,3);
end
if i<M&j<N&Gray(i,j)==m-1&Gray(i+1,j+1)==n-1
P(m,n,4) = P(m,n,4)+1;
P(n,m,4) = P(m,n,4);
end
end
end
if m==n
P(m,n,:) = P(m,n,:)*2;
end
end
end
%%---------------------------------------------------------
% 对共生矩阵归一化
%%---------------------------------------------------------
for n = 1:4
P(:,:,n) = P(:,:,n)/sum(sum(P(:,:,n)));
end
%--------------------------------------------------------------------------
%4.对共生矩阵计算能量、熵、惯性矩、相关4个纹理参数
%--------------------------------------------------------------------------
H = zeros(1,4);
I = H;
Ux = H; Uy = H;
deltaX= H; deltaY = H;
C =H;
for n = 1:4
E(n) = sum(sum(P(:,:,n).^2)); %%能量
for i = 1:16
for j = 1:16
if P(i,j,n)~=0
H(n) = -P(i,j,n)*log(P(i,j,n))+H(n); %%熵
end
I(n) = (i-j)^2*P(i,j,n)+I(n); %%惯性矩
Ux(n) = i*P(i,j,n)+Ux(n); %相关性中μx
Uy(n) = j*P(i,j,n)+Uy(n); %相关性中μy
end
end
end
for n = 1:4
for i = 1:16
for j = 1:16
deltaX(n) = (i-Ux(n))^2*P(i,j,n)+deltaX(n); %相关性中σx
deltaY(n) = (j-Uy(n))^2*P(i,j,n)+deltaY(n); %相关性中σy
C(n) = i*j*P(i,j,n)+C(n);
end
end
C(n) = (C(n)-Ux(n)*Uy(n))/deltaX(n)/deltaY(n); %相关性
end
%--------------------------------------------------------------------------
%求能量、熵、惯性矩、相关的均值和标准差作为最终8维纹理特征
%--------------------------------------------------------------------------
a1 = mean(E)
b1 = sqrt(cov(E))
a2 = mean(H)
b2 = sqrt(cov(H))
a3 = mean(I)
b3 = sqrt(cov(I))
a4 = mean(C)
b4 = sqrt(cov(C))
sprintf('0,45,90,135方向上的能量依次为: %f, %f, %f, %f',E(1),E(2),E(3),E(4)) % 输出数据;
sprintf('0,45,90,135方向上的熵依次为: %f, %f, %f, %f',H(1),H(2),H(3),H(4)) % 输出数据;
sprintf('0,45,90,135方向上的惯性矩依次为: %f, %f, %f, %f',I(1),I(2),I(3),I(4)) % 输出数据;
sprintf('0,45,90,135方向上的相关性依次为: %f, %f, %f, %f',C(1),C(2),C(3),C(4)) % 输出数据;
灰度共生矩阵只是描述纹理的一种方法,其本身是不能作为特征的.
特别是灰度等级大的时候.
但是灰度共生矩阵的能量相关等二次特征可以表征图像的一些特性.
问题一:接下来然后怎么办?
接下来转化为其它的特征作为输入.
问题二:一副图像的纹理特征提取出来的矩阵和原来矩阵的维数是相同的还是不同的?
一般不是相同的,一般要小,特征嘛,要不然不需要降维,直接让原图像作为原始特征.
一般是需要降维的,matlab中灰度共生矩阵函数中有降维的操作吗,还是需要自己写进去这些代码才会有降维发生?
非你有降维的操作,不然肯定是相同的!你若是理解了共生矩阵怎么得来的也就完全明白了~~
Gray-level co-occurrence matrix from an image
图像的灰度共生矩阵
灰度共生矩阵是像素距离和角度的矩阵函数,它通过计算图像中一定距离和一定方向的两点灰度之间的相关性,来反映图像在方向、间隔、变化幅度及快慢上的综合信息。
使用方法:
glcm = graycomatrix(I)
glcms = graycomatrix(I,param1,val1,param2,val2,...)
[glcms,SI] = graycomatrix(...)
描述:
glcms = graycomatrix(I) 产生图像I的灰度共生矩阵GLCM。它是通过计算两灰度值在图像I中水平相邻的次数而得到的 (也不必是水平相邻的次数,这一参数是可调的,可能通过Offsets来进行调整,比如[0 D]代表是水平方向,[-D D]代表是右上角45度方向,[-D 0]代表是竖直方向,即90度方向,而[-D -D]则代表是左上角,即135度方向),GLCM中的每一个元素(i,j)代表灰度i与灰度j在图像中水平相邻的次数。
因为动态地求取图像的GLCM区间代价过高,我们便首先将灰度值转换到I的灰度区间里。如果I是一个二值图像,那么灰度共生矩阵就将图像转换到两级。如果I是一个灰度图像,那将转换到8级。灰度的级数决定了GLCM的大小尺寸。你可以通过设定参数“NumLevels”来指定灰度的级数,还可以通过设置“GrayLimits"参数来设置灰度共生矩阵的转换方式。
下图显示了如何求解灰度共生矩阵,以(1,1)点为例,GLCM(1,1)值为1说明只有一对灰度为1的像素水平相邻。GLCM(1,2)值为2,是因为有两对灰度为1和2的像素水平相邻。
glcms = graycomatrix(I,param1,val1,param2,val2,...) 返回一个或多个灰度灰度共生矩阵,根据指定的参数。参数可以很简短,并且对大小写不敏感。
参数
'GrayLimits' 是两个元素的向量,表示图像中的灰度映射的范围,如果其设为[],灰度共生矩阵将使用图像I的最小及最大灰度值作为GrayLimits
'NumLevels' 一个整数,代表是将图像中的灰度归一范围。举例来说,如果NumLevels为8,意思就是将图像I的灰度映射到1到8之间,它也决定了灰度共生矩阵的大小
'Offset' 上面有解释,是一个p*2的整数矩阵,D代表是当前像素与邻居的距离,通过设置D值,即可设置角度
Angle Offset
0 [0 D]
45 [-D D]
90 [-D 0]
135 [-D -D]
示例:
计算灰度共生矩阵,并且返回缩放后的图像,SI
I = [ 1 1 5 6 8 8; 2 3 5 7 0 2; 0 2 3 5 6 7];
[glcm,SI] = graycomatrix(I,'NumLevels',9,'G',[])
计算灰度图像的灰度共生矩阵
I = imread('circuit.tif');
glcm = graycomatrix(I,'Offset',[2 0]);
灰度共生矩阵的特征:
角二阶矩(Angular Second Moment, ASM)
ASM=sum(p(i,j).^2) p(i,j)指归一后的灰度共生矩阵
角二阶矩是图像灰度分布均匀程度和纹理粗细的一个度量,当图像纹理绞细致、灰度分布均匀时,能量值较大,反之,较小。
熵(Entropy, ENT)
ENT=sum(p(i,j)*(-ln(p(i,j)))
是描述图像具有的信息量的度量,表明图像的复杂程序,当复杂程序高时,熵值较大,反之则较小。
反差分矩阵(Inverse Differential Moment, IDM)
IDM=sum(p(i,j)/(1+(i-j)^2))
反映了纹理的清晰程度和规则程度,纹理清晰、规律性较强、易于描述的,值较大;杂乱无章的,难于描述的,值较小。
http://blog.csdn.net/weiyuweizhi/article/details/5724050
http://apps.hi.baidu.com/share/detail/19780877
灰度共生矩阵法,顾名思义,就是通过计算灰度图像得到它的共生矩阵,然后透过计算这个共生矩阵得到矩阵的部分特征值,来分别代表图像的某些纹理特征(纹理的定义仍是难点)。灰度共生矩阵能反映图像灰度关于方向、相邻间隔、变化幅度的综合信息,它是分析图像的局部模式和它们排列规则的基础。
对于灰度共生矩阵的理解,需要明确几个概念:方向,偏移量和灰度共生矩阵的阶数。
1、 方向
一般计算过程会分别选在几个不同的方向来进行,常规的是0°、45°、90°、135°,理论上的所有方向计算方法不可取。
定义如下:
水平方向为0°垂直的90°,以及45°和135°(大致如上图所画)
2、偏移量(offset:下面例子中,取值为1来帮助理解)
3、灰度共生矩阵的阶数和灰度图像的灰度值的阶数是一致的,即当灰度图像的灰度值的阶数是N时,灰度共生矩阵为N*N的矩阵。
|
0 |
0 |
0 |
1 |
2 |
|
0 |
0 |
1 |
1 |
2 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
2 |
2 |
1 |
|
1 |
2 |
2 |
1 |
0 |
假定offset为1,取0°方向求共生矩阵时:
最初取点(1,1) 和(1,2) ,此时在频度矩阵的(0,0)处加1((1,1)点的灰度值为0,(1,2)点的灰度也为0);
然后取(1,2) 和(1,3)点,此时也在频度矩阵的(0,0)处加1;
接着取到(1,3) 和(1,4)点,此时也在频度矩阵的(0,0)处加1;
接着取到(1,4) 和(1,5) 点,此时在频度矩阵的(1,0)处加1((1,5)点的灰度值为1 ,(1,4)点的灰度为0)。
直到每一行都取遍即可。
假定offset为1,取45°方向求共生矩阵时:
最初取点(1,1) 和(2,2) ,此时在45°方向频度矩阵的(0,0)处加1((1,1)点的灰度值为0,(2,2)点的灰度也为0);
然后取(1,2) 和(2,3)点,此时在45°方向频度矩阵的(0,1)处加1;
接着取到(1,3) 和(2,4)点,此时也在45°方向频度矩阵的(0,1)处加1;
接着取到(1,4) 和(2,5) 点,此时在45°方向频度矩阵的(1,2)处加1((1,4)点的灰度值为1,(2,5)点的灰度为2)。
然后下一行,直到每一行合适的值都取遍即可。
另两个方向的情况相似。
最后得到如下四个频度矩阵
|
10 |
0 |
1 |
2 |
|
0 |
3 |
3 |
0 |
|
1 |
1 |
5 |
4 |
|
2 |
0 |
2 |
2 |
|
11 |
0 |
1 |
2 |
|
0 |
1 |
5 |
0 |
|
1 |
0 |
3 |
5 |
|
2 |
1 |
1 |
0 |
0°方向频度矩阵 45°方向频度矩阵
|
10 |
0 |
1 |
2 |
|
0 |
3 |
3 |
0 |
|
1 |
1 |
6 |
3 |
|
2 |
0 |
2 |
2 |
|
10 |
0 |
1 |
2 |
|
0 |
3 |
0 |
0 |
|
1 |
0 |
7 |
2 |
|
2 |
0 |
2 |
2 |
90°方向频度矩阵 135°方向频度矩阵
在用matlab编程时由于matlab的矩阵的下脚标是从1开始的所以矩阵的形式类似于下面的形式:
p(I(i,j)+1,I(i,j+1)+1)= p(I(i,j)+1,I(i,j+1)+1)+1;这是0°方向的计算式
这里,灰度阶数即从最低的0变成最低为1
四个方向的计算式,大致如下:
p1(IN(M,N)+1,IN(M,N+1)+1)= p1(IN(M,N)+1,IN(M,N+1)+1)+1;%是共生矩阵0度的计算式
p1(IN(M,N)+1,IN(M-1,N+1)+1)= p1(IN(M,N)+1,IN(M-1,N+1)+1)+1;%是45度的计算式
p1(IN(M,N)+1,IN(M-1,N)+1)= p1(IN(M,N)+1,IN(M-1,N)+1)+1;%是共生矩阵90度的计算式
p1(IN(M,N)+1,IN(M-1,N-1)+1)= p1(IN(M,N)+1,IN(M-1,N-1)+1)+1;%是135度的计算式
现在各个方向统计完毕,然后将频度矩阵/总频次即得共生矩阵
这时候得到四个共生矩阵,分别是、
、
、
其编程实现,可参见如下代码:
%2.为了减少计算量,对原始图像灰度级压缩,将Gray量化成16级
%--------------------------------------------------------------------------
for i = 1:M
for j = 1:N
for n = 1:256/16
if (n-1)*16<=Gray(i,j)&Gray(i,j)<=(n-1)*16+15
Gray(i,j) = n-1;
end
end
end
end
%--------------------------------------------------------------------------
%3.计算四个共生矩阵P,取距离为1,角度分别为0,45,90,135
%--------------------------------------------------------------------------
P = zeros(16,16,4);
for m = 1:16
for n = 1:16
for i = 1:M
for j = 1:N
if j<N&Gray(i,j)==m-1&Gray(i,j+1)==n-1
P(m,n,1) = P(m,n,1)+1;
P(n,m,1) = P(m,n,1);
end
if i>1&j<N&Gray(i,j)==m-1&Gray(i-1,j+1)==n-1
P(m,n,2) = P(m,n,2)+1;
P(n,m,2) = P(m,n,2);
end
if i<M&Gray(i,j)==m-1&Gray(i+1,j)==n-1
P(m,n,3) = P(m,n,3)+1;
P(n,m,3) = P(m,n,3);
end
if i<M&j<N&Gray(i,j)==m-1&Gray(i+1,j+1)==n-1
P(m,n,4) = P(m,n,4)+1;
P(n,m,4) = P(m,n,4);
end
end
end
if m==n
P(m,n,:) = P(m,n,:)*2;
end
end
end
%%---------------------------------------------------------
% 对共生矩阵归一化
%%---------------------------------------------------------
for n = 1:4
P(:,:,n) = P(:,:,n)/sum(sum(P(:,:,n)));
end