灰度共生矩阵是像素距离和角度的矩阵函数,它通过计算图像中一定距离和一定方向的两点灰度之间的相关性,来反映图像在方向、间隔、变化幅度及快慢上的综合信息。
使用方法:
glcm = graycomatrix(I)
glcms = graycomatrix(I,param1,val1,param2,val2,...)
[glcms,SI] = graycomatrix(...)
描述:
glcms = graycomatrix(I) 产生图像I的灰度共生矩阵GLCM。它是通过计算两灰度值在图像I中水平相邻的次数而得到的 (也不必是水平相邻的次数,这一参数是可调的,可能通过Offsets来进行调整,比如[0 D]代表是水平方向,[-D D]代表是右上角45度方向,[-D 0]代表是竖直方向,即90度方向,而[-D -D]则代表是左上角,即135度方向),GLCM中的每一个元素(i,j)代表灰度i与灰度j在图像中水平相邻的次数。
因为动态地求取图像的GLCM区间代价过高,我们便首先将灰度值转换到I的灰度区间里。如果I是一个二值图像,那么灰度共生矩阵就将图像转换到两级。如果I是一个灰度图像, 那将转换到8级。灰度的级数决定了GLCM的大小尺寸。你可以通过设定参数“NumLevels”来指定灰度的级数,还可以通过设置“GrayLimits"参数来设置灰度共生矩阵的转换方式。
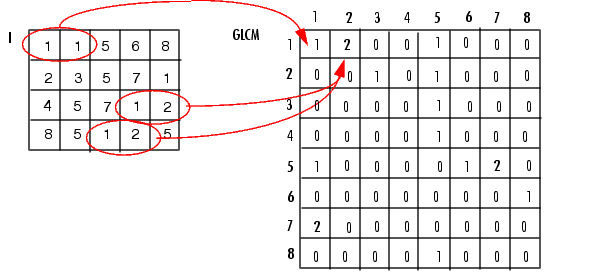
下图显示了如何求解灰度共生矩阵,以(1,1)点为例,GLCM(1,1)值为1说明只有一对灰度为1的像素水平相邻。GLCM(1,2)值为2,是因为有两对灰度为1和2的像素水平相邻。
glcms = graycomatrix(I,param1,val1,param2,val2,...) 返回一个或多个灰度灰度共生矩阵,根据指定的参数。参数可以很简短,并且对大小写不敏感。
参数
'GrayLimits' 是两个元素的向量,表示图像中的灰度映射的范围,如果其设为[],灰度共生矩阵将使用图像I的最小及最大灰度值作为GrayLimits
'NumLevels' 一个整数,代表是将图像中的灰度归一范围。举例来说,如果NumLevels为8,意思就是将图像I的灰度映射到1到8之间,它也决定了灰度共生矩阵的大小
'Offset' 上面有解释,是一个p*2的整数矩阵,D代表是当前像素与邻居的距离,通过设置D值,即可设置角度
Angle Offset
0 [0 D]
45 [-D D]
90 [-D 0]
135 [-D -D]
示例:
计算灰度共生矩阵,并且返回缩放后的图像,SI
I = [ 1 1 5 6 8 8; 2 3 5 7 0 2; 0 2 3 5 6 7];
[glcm,SI] = graycomatrix(I,'NumLevels',9,'G',[])
计算灰度图像的灰度共生矩阵
I = imread('circuit.tif');
glcm = graycomatrix(I,'Offset',[2 0]);
灰度共生矩阵的特征:
角二阶矩(Angular Second Moment, ASM)
ASM=sum(p(i,j).^2) p(i,j)指归一后的灰度共生矩阵
角二阶矩是图像灰度分布均匀程度和纹理粗细的一个度量,当图像纹理绞细致、灰度分布均匀时,能量值较大,反之,较小。
熵(Entropy, ENT)
ENT=sum(p(i,j)*(-ln(p(i,j)))
是描述图像具有的信息量的度量,表明图像的复杂程序,当复杂程序高时,熵值较大,反之则较小。
反差分矩阵(Inverse Differential Moment, IDM)
IDM=sum(p(i,j)/(1+(i-j)^2))
反映了纹理的清晰程度和规则程度,纹理清晰、规律性较强、易于描述的,值较大;杂乱无章的,难于描述的,值较小。