开头先放题目。防止走错》》》》
这道题呢，poj对我们英语不好的人简直不友好（百度翻译-> https://fanyi.baidu.com/）。
首先先说一下题意，n个点，由m条双向路连接。求从同一点开始结束的一条最短路。如果有好几条就随意输出一条（Special Judge 随便浪啊~）。
看到这道题，我的第一反应就是求最短路。然而如果直接求的话.......是0没错。所以，我们要找的其实是最小环。
而，一般的解决方法自然就是dijkstra：说实话，我没写过，不知道好不好写QAQ（闲的无聊你可以试试啊）。
我们把任意两个有边相连的结点i j的直接距离加上i j间不包含边(边i -> j)的最短路径当做一个环的权。
所以呢？好像求最短路径我们第一个想到的就是Dijkstra算法啊。然而Dijkstra所求的是一个点到所有点的最短距离。这个最短距离一定是ij的直接距离(如果i j连通)。
因此我们可以先将i j的边从图中删除(若i j不连通，就当然不用删除啦)，然后再用Dijkstra求新图中i、j的最短距离即可。
解决方法就出来了：我们每次在图中选取一条边，把它从图中删掉．然后对删掉的那条边所对应的2个点去进行Dijkstra，也就是m次Dijkstra。
然而，对不起，好慢。拒绝。逃】
所以介绍一个小东西（其实我也是刚学的，逃】）听说这玩意叫Folyd求最小环？？（管他叫啥，会用就行了QAQ）这里简单讲解一下。
Floyd->最小环？
基本的判环应该懂吧？（不懂的话，请点右上角的 X 谢谢）
那么，对于一个最小环（至少三个点），那么肯定有一个点与左右两侧的点是直接连接的(即不经其他点的松弛)。所以呢，我们来证明一下。
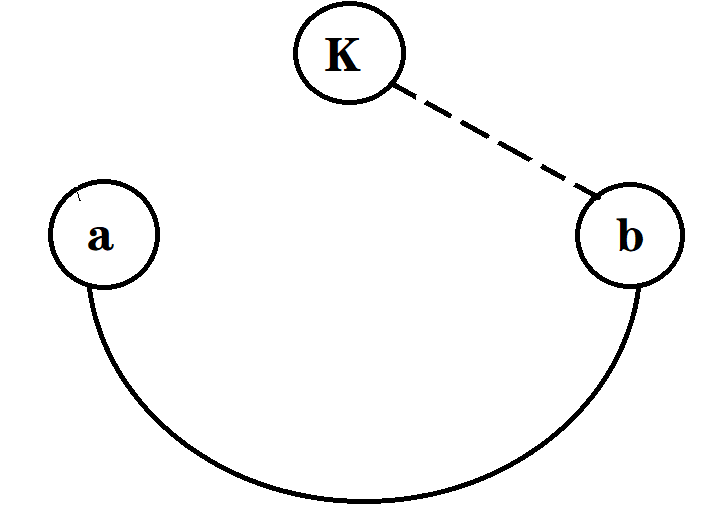该图假设a<b<k，且ab间的路已找出（无环）。
首先假设k是会更新a点的最短路的最新点。我们看这个图，由于k点是最大的，而Floyd是从较小的点来循环的，所以可以保证是第一个环（最小）。所以这个小技巧其实就是裸的Floyd加一个记录路径啊。
Floyd的板子？（我没写过所以给你们copy一个同组大佬的）
void Floyd() { for(int k=0;k<n;++k) for(int i=0;i<n;++i) for(int j=0;j<n;++j) dj[i][j] = min(dj[i][j],dj[i][k]+dj[k][j]); }
所以接下来如何记录路径..........?
第一种写法（开数组记录）：
先开一个矩阵pre，它的定义是这样的：pre(ij)的值如果为p，就表示i到j的最短行经为i->p...->j。也就是说p就是i到j的最短行径中的j之前的第1个点。 然后就好做啦！
对于i j来说找出pre(i j)，值为p，就知道了路径i->p...->j；再去找pre(p j)，如果值为q，p到j的最短路径为p->q...->j；再去找pre(qj)，如果值为r，i到q的最短路径为q>r...-
>q；所以一再反复，就会得到答案。（如果你不会写？？那就慢走不送）
放代码。
if((dis[i][j]+mp[j][k]+mp[k][i])<minn) { minn=dis[i][j]+mp[j][k]+mp[k][i]; cnt=0; num[++cnt]=k; int sl=j; while(sl!=i) { num[++cnt]=sl; sl=pre[i][sl]; } num[++cnt]=i; }
（代码极丑，不要照抄谢谢QAQ）
然后是第二种方法dfs回溯：
这个就好理解多了吧........那我就一句带过啦。
void get(int x,int y) { int mid=pre[x][y]; if(!mid){ path[num++]=y; return ; } get(x,mid); get(mid,y); }
最后放上完整代码（因为我写的只有第一种方法，所以自然就只放一个啦）
#include<iostream> #include<cstring> #include<cstdio> #include<cmath> #include<queue> #include<algorithm> using namespace std; const int inf=9999999; const int MA=105; int n,m,minn,cnt; int mp[MA][MA],dis[MA][MA],pre[MA][MA],num[105]; void floyd() { minn=inf; for(int k=1;k<=n;k++) { for(int i=1;i<k;i++) for(int j=i+1;j<k;j++) if((dis[i][j]+mp[j][k]+mp[k][i])<minn) { minn=dis[i][j]+mp[j][k]+mp[k][i]; cnt=0; num[++cnt]=k; int sl=j; while(sl!=i) { num[++cnt]=sl; sl=pre[i][sl]; } num[++cnt]=i; } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(dis[i][j]>(dis[i][k]+dis[k][j])) { dis[i][j]=dis[i][k]+dis[k][j]; pre[i][j]=pre[k][j]; } } return; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { pre[i][j]=i; if(i==j) mp[i][j]=dis[i][j]=0; else mp[i][j]=dis[i][j]=inf; } for(int i=1;i<=m;i++) { int a,b,c; scanf("%d%d%d",&a,&b,&c); mp[a][b]=min(mp[a][b],c); mp[b][a]=min(mp[b][a],c); dis[b][a]=min(dis[a][b],c); dis[a][b]=min(dis[b][a],c); } floyd(); if(minn==inf) cout<<"No solution."<<endl; else for(int i=cnt;i>=1;i--) cout<<num[i]<<" "; return 0; }
写的极丑，一看就是我的风格！！
最后放上数据...（好像刚刚忘了 逃】）.....
因为博客好难写所以中间有不雅语言请见谅（我懒的删了），拜拜！