1.非线性规划的形式:
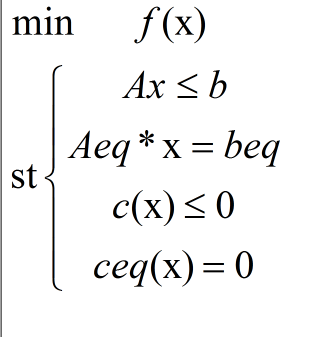
其中x是一个列向量,st中前两项为线性约束条件,后两项为非线性约束条件。
在MATLAB中fmincon是用于求解非线性多远函数的最小值的函数,这里介绍fmincon的其中一种语法格式:
[x,fval,exitflag,output]=fmincon[目标函数f(x)调用,x的初值,A,b,Aeq,beq,lb,ub,非线性约束函数调用]。
如果最终算出的exitflag=1,即过程成功收敛的话,x的初值在赋值时是不受影响的。
且:
1----A,b,Aeq,beq分别为线性约束条件不等式的系数矩阵,线性约束条件不等式中的右值,线性约束条件灯饰的系数矩阵和线性约束条件等式中的右值。lb,ub分别为x的最小值和x的最大值。以上如果有不存在的项用[]表示。
2----fmincon需要用到函数的调用
建立目标函数方式如下:a.新建一个m文件,作为目标函数的存放地点。
b.输入:function f=文件名(x)【这里f是函数返回的函数值,x是一个列向量】
f=目标函数f(x)
end
c.【点击保存时文件会自动改成在a步设置的名字】
封装非线性的约束函数方式如下:a.新建一个m文件,作为非线性的约束函数的封装地点。
b.输入: function [h,g]=文件名(x)
h=c(x)
g=ceq(x)
end
c.【此处h为非线性不等式的约束条件,g为非线性等式的约束条件。当约束条件不止一个是可以写成h(1),h(2)...,g(1),g(2)...的形式。同理,x代表一个列向量,当列向量有多个元素时也要写成x(1),x(2)的形式。】
下面举个例子:
.
程序:
1.目标函数的引用:文件:myfun1.m
function f=myfun1(x)【注意这个地方后面不能加分号】
f=x(1)^2+x(2)^2+8;
end
2.非线性约束函数的引用:文件:myfun2.m()
function [h,g]=myfun2(x)
h=-x(1)^2+x(2);
g=-x(1)-x(2)^2+2;
end
以上的x都代表向量[x1,x2],但不能这样写
主函数:
[x,fval,exitflag,output]=fmincon('myfun1',[0 1],[],[],[],[],zeros(2,1),[],'myfun2')
运行结果:
x =
1.0000 1.0000
fval =
10
exitflag =
1
output =
iterations: 8
funcCount: 36
stepsize: 1
algorithm: 'medium-scale: SQP, Quasi-Newton, line-search'
firstorderopt: 1.3655e-007
cgiterations: []
message: [1x144 char]