题目背景
本题中合法括号串的定义如下:
()是合法括号串。- 如果
A是合法括号串,则(A)是合法括号串。 - 如果
A,B是合法括号串,则AB是合法括号串。
本题中子串与不同的子串的定义如下:
- 字符串
S的子串是S中连续的任意个字符组成的字符串。S的子串可用起始位置 (l) 与终止位置 (r) 来表示,记为 S (l, r)((1 leq l leq r leq |S |)(|S |) 表示 (S) 的长度)。 S的两个子串视作不同当且仅当它们在S中的位置不同,即 (l) 不同或 (r) 不同。
题目描述
一个大小为 (n) 的树包含 (n) 个结点和 (n − 1) 条边,每条边连接两个结点,且任意两个结点间有且仅有一条简单路径互相可达。
小 (Q) 是一个充满好奇心的小朋友,有一天他在上学的路上碰见了一个大小为 (n) 的树,树上结点从 (1) ∼ (n) 编号,(1) 号结点为树的根。除 (1) 号结点外,每个结点有一个父亲结点,(u)((2 leq u leq n))号结点的父亲为 (f_u)((1 ≤ f_u < u))号结点。
小 (Q) 发现这个树的每个结点上恰有一个括号,可能是( 或)。小 (Q) 定义 (s_i) 为:将根结点到 (i) 号结点的简单路径上的括号,按结点经过顺序依次排列组成的字符串。
显然 (s_i) 是个括号串,但不一定是合法括号串,因此现在小 (Q) 想对所有的 (i)((1leq ileq n))求出,(s_i) 中有多少个互不相同的子串是合法括号串。
这个问题难倒了小 (Q),他只好向你求助。设 (s_i) 共有 (k_i) 个不同子串是合法括号串, 你只需要告诉小 Q 所有 (i imes k_i) 的异或和,即:
((1 imes k_1) ext{xor} (2 imes k_2) ext{xor} (3 imes k_3) ext{xor} cdots ext{xor} (n imes k_n))
其中 (xor) 是位异或运算。
输入格式
第一行一个整数 (n),表示树的大小。
第二行一个长为 (n) 的由( 与) 组成的括号串,第 (i) 个括号表示 (i) 号结点上的括号。
第三行包含 (n − 1) 个整数,第 (i)((1 leq i lt n))个整数表示 (i + 1) 号结点的父亲编号 (f_{i+1})。
输出格式
仅一行一个整数表示答案。
输入输出样例
输入 #1
5
(()()
1 1 2 2
输出 #1
6
说明/提示
【样例解释1】
树的形态如下图:
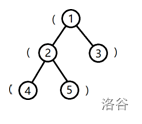
将根到 (1) 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 (,子串是合法括号串的个数为 (0)。
将根到 (2) 号结点的字符串为 ((,子串是合法括号串的个数为 (0)。
将根到 (3) 号结点的字符串为 (),子串是合法括号串的个数为 (1)。
将根到 (4) 号结点的字符串为 (((,子串是合法括号串的个数为 (0)。
将根到 (5) 号结点的字符串为 ((),子串是合法括号串的个数为 (1)。
【数据范围】
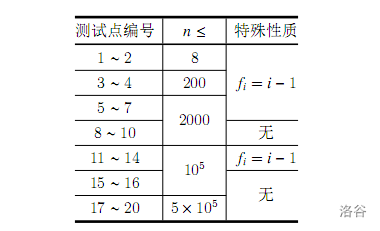
明显的树形(DP)。
思路有点难讲。花了考场上(1.5h)想出来的。
先考虑暴力。我们需要一个能过(50pts)的暴力,所以对于每一个节点,我们必须在最多(O(n))的时间处理出答案贡献。
考虑类似单调性优化的方法。容易想到,对于一个点(u)的父亲,当它转移到(u)时,所增加的合法子串数量只有这个括号加上从这个点到之前链上所有括号的匹配情况。
比如说我们加了一个右括号,我只需要往回搜索所有合法的每个链上的左括号即可。由此,我们需要用(O(1))的时间检查每个左括号是否能对新加入的右括号作出贡献。
我们需要用一个栈记录所有没有匹配过的右括号。每次遇到一个右括号就把它进栈;每次遇到左括号如果栈空直接(break),因为再往前搜的字串一定经过这个不可能匹配到的左括号;否则把它出栈,如果出栈之后栈空说明从这个位置到新加入的位置恰好构成一个合法串,答案加一。
这个复杂度是(O(n))的主要原因是对于每一个点必须扫描所有前面的点,这个过程效率实在太低。考虑优化这个过程。
对于每一个新进入栈的右括号,能对答案做出的贡献只有两种情况:
第一,找到了从当前位置往根节点方向走第一个没有匹配的左括号,这样从这个左括号到当前位置一定是合法的子串,因为这两个括号之间所有的左括号一定匹配了一个子串上的右括号。
第二,第一个没有匹配的左括号前面紧挨着它的合法子串可以和第一种情况的子串共同构成新的合法子串,而紧挨着当前链上第一个没有匹配的左括号的位置一定是固定的。
上面两种情况加起来得到了这个有括号的总计答案。
考虑设计(dp)转移状态。从第二部分入手,我们发现因为用来转移的位置是固定的(它紧挨着当前链上第一个没有匹配的左括号),当前加入点的位置也是固定的,考虑将前者作为后者的子问题。所以我们得到,用(dp[i])表示从根节点走到点(i)的链上严格以(i)结尾的合法子串数目。
同时我们需要维护“第一个没有匹配的左括号的位置”,所以可以借助暴力的思路使用一个栈。用栈顶表示当前链上第一个没有匹配的左括号的位置,每次遇到一个左括号进栈并标记(dp[i]=0),遇到一个右括号时如果栈为空则标记(dp[i]=0)因为没有可以和它匹配的左括号;否则弹出栈顶,标记(dp[i]=dp[fa[s[top]]]+1)。那个加上的(1)表示这个加入的右括号和第一个没有匹配的左括号匹配上的子串,这个没有匹配的左括号是(s[top]);所以(fa[s[top]])表示紧挨着它的第一个括号,即(dp[fa[s[top]]])表示这个位置对应上述第二种情况。因为从这个点走到根节点且以这个点结尾的合法子串数目恰好每个合法子串都可以和上面那个加上的(1)组成一个新的子串。
比如说,从()(变成()(),新加入的右括号在对应那个没有匹配的左括号同时,这个括号对又能和前面匹配好的()组成新的合法串()()。
注意一个问题。因为我们全局只使用一个栈,所以我们当搜完一棵子树并回溯的时候必须恢复栈的状态到刚搜到这个点时的状态。所以我们考虑递归地恢复状态。对于每次搜索我们只有进栈/出栈两种可能,所以如果(dp)这个点进过栈,我们就将其弹出;如果出过栈我们就重新进栈。
代码。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<stack>
#define int long long
#define rep(i,a,n) for(register int i=a;i<=n;++i)
#define dwn(i,n,a) for(register int i=n;i>=a;--i)
using namespace std;
int n,head[500050],num,f[500050],dp[500050],ans;
stack<int> s;
char str[500050];
struct edge
{
int u,v,nxt;
}e[1000050];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void write(int x)
{
if(x<0)putchar('-'),x=-x;
if(x==0)return;
write(x/10);
putchar('0'+x%10);
}
void add(int u,int v)
{
e[++num].u=u;e[num].v=v;
e[num].nxt=head[u];head[u]=num;
}
void DP(int x,int fa,int cost)
{
int flag=0;
if(str[x]=='(')s.push(x);
else
{
if(s.empty())dp[x]=0;
else
{
flag=s.top();//如果有过出栈操作就再进去
s.pop();
dp[x]=dp[f[flag]]+1;
}
}
for(register int st=head[x];~st;st=e[st].nxt)
{
int y=e[st].v;
if(y==fa)continue;
DP(y,x,cost+dp[x]);
}
if(flag)s.push(flag);//恢复
ans^=x*(cost+dp[x]);//cost记录不算这个点的答案
if(str[x]=='(')s.pop();//只有这个点是'('才进过栈
return;
}
signed main()
{
memset(head,-1,sizeof head);
n=read();
cin>>(str+1);
rep(i,2,n)
{
f[i]=read();
add(i,f[i]);
add(f[i],i);
}
DP(1,-1,0);
if(ans)write(ans);
else putchar('0');
return 0;
}
/*
7
(()))((
1 2 1 2 5 3
*/