题目描述
话说,中中带领的OIER们打算举行一次冬季泼水节,当然这是要秘密进行的,绝对不可以让中中知道。不过中中可是老江湖了,当然很快就发现了我们的小阴谋,于是他准备好水枪迫不及待的想要加入我们了。
我们一共有N个OIER打算参加这个泼水节,同时很凑巧的是正好有N个水龙头(至于为什么,我不解释)。N个水龙头之间正好有N-1条小道,并且每个水龙头都可以经过小道到达其他水龙头(这是一棵树,你应该懂的..)。但是OIER门为了迎接中中的挑战,决定修建一些个道路(至于怎么修,秘密~),使得每个水龙头到每个水龙头之间都有一条直接的道路连接(也就是构成一个完全图呗~)。但是OIER门很懒得,并且记性也不好,他们只会去走那N-1条小道,并且希望所有水龙头之间修建的道路,都要大于两个水龙头之前连接的所有小道(小道当然要是最短的了)。所以神COW们,帮那些OIER们计算一下吧,修建的那些道路总长度最短是多少,毕竟修建道路是要破费的~~
我们一共有N个OIER打算参加这个泼水节,同时很凑巧的是正好有N个水龙头(至于为什么,我不解释)。N个水龙头之间正好有N-1条小道,并且每个水龙头都可以经过小道到达其他水龙头(这是一棵树,你应该懂的..)。但是OIER门为了迎接中中的挑战,决定修建一些个道路(至于怎么修,秘密~),使得每个水龙头到每个水龙头之间都有一条直接的道路连接(也就是构成一个完全图呗~)。但是OIER门很懒得,并且记性也不好,他们只会去走那N-1条小道,并且希望所有水龙头之间修建的道路,都要大于两个水龙头之前连接的所有小道(小道当然要是最短的了)。所以神COW们,帮那些OIER们计算一下吧,修建的那些道路总长度最短是多少,毕竟修建道路是要破费的~~
输入
本题为多组数据~
第一行t,表示有t组测试数据
对于每组数据
第一行N,表示水龙头的个数(当然也是OIER的个数);
2到N行,每行三个整数X,Y,Z;表示水龙头X和水龙头Y有一条长度为Z的小道
第一行t,表示有t组测试数据
对于每组数据
第一行N,表示水龙头的个数(当然也是OIER的个数);
2到N行,每行三个整数X,Y,Z;表示水龙头X和水龙头Y有一条长度为Z的小道
输出
对于每组数据,输出一个整数,表示修建的所有道路总长度的最短值。
样例输入
2
3
1 2 2
1 3 3
4
1 2 3
2 3 4
3 4 5
样例输出
4
17
提示
【数据范围】
每个测试点最多10组测试数据
50% n<=1500;
100% n<=6000
100% z<=100
【样例解释】
第一组数据,在2和3之间修建一条长度为4的道路,是这棵树变成一个完全图,且原来的树依然是这个图的唯一最小生成树.
每个测试点最多10组测试数据
50% n<=1500;
100% n<=6000
100% z<=100
【样例解释】
第一组数据,在2和3之间修建一条长度为4的道路,是这棵树变成一个完全图,且原来的树依然是这个图的唯一最小生成树.
题意还是很不可理喻好理解的 就是给你一棵树让它是一个完全图的最小生成树 让这个完全图的边权和最小
按照Kruscal的方法 我们可以知道 当在一个完全图中做最小生成树的时候 连接两个集合的边一定是所有连接两个集合元素最短的边
大概就是这个意思
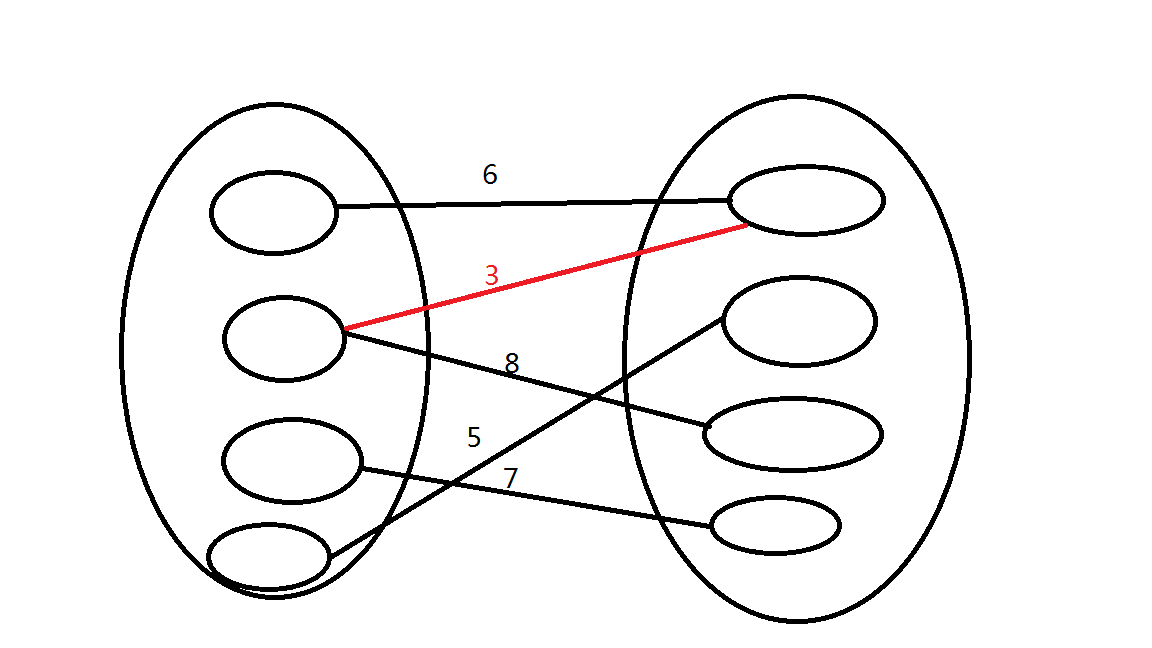
在连接左右两个集合时 我们应该选那条红色的边 也就是说 这条红色的边一定是唯一一条可能存在于最小生成树上的连接这两个集合的边
但是 现在已经给定了最小生成树上所有的边 也就是给定了所有连接两个集合的最短边 我们就可以通过逆向构造其它边的方式完成这个完全图
刚才说过什么?最小生成树上所有的边一定是连接这两个集合的最短边
假设连接A、B两个集合的最短边(这条边在最小生成树上)长度为l 那很明显连接A与B其它元素的边的长度至少为l+1
而完全图保证每两个元素之间都有直接连接的边 假设A中有n个元素 B中有m个元素 则长度至少为l+1的边有n*m-1条
即可把(l+1)*(n+m-1)贡献到答案中
上代码
#include<iostream> #include<algorithm> #include<cstring> using namespace std; int t,n,fa[6050],book[6050]; struct edge { int u,v,c; }; bool cmp(edge a,edge b) { return a.c<b.c; }//按边权排序 int f(int o) { if(fa[o]==o)return o; return fa[o]=f(fa[o]); } void u(int a,int b) { if(a<b)book[f(a)]+=book[f(b)],fa[f(b)]=fa[f(a)]; else book[f(b)]+=book[f(a)],fa[f(a)]=fa[f(b)]; } int main() { scanf("%d",&t); while(t--) { int ans=0; memset(fa,0,sizeof fa); memset(book,0,sizeof book); scanf("%d",&n); edge e[6050]; for(int i=1;i<=n-1;i++)scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].c); sort(e+1,e+n,cmp); for(int i=1;i<=n;i++)fa[i]=i,book[i]=1; for(int i=1;i<=n-1;i++) { ans+=(book[f(e[i].u)]*book[f(e[i].v)]-1)*(e[i].c+1); u(e[i].u,e[i].v);//Kruscal } printf("%d ",ans); } return 0; }