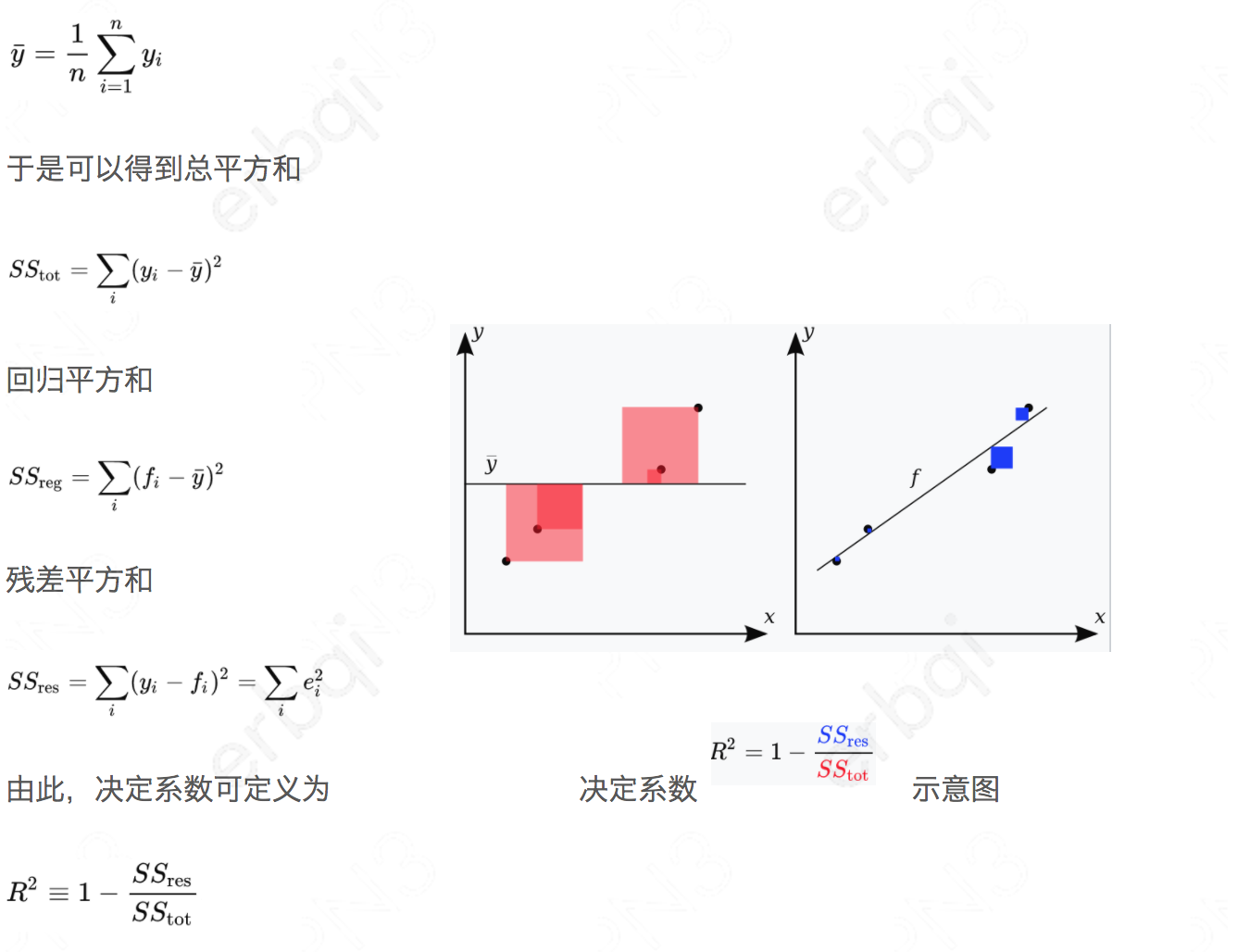
决定系数(coefficient of determination,R2)是反映模型拟合优度的重要的统计量,为回归平方和与总平方和之比。R2取值在0到1之间,且无单位,其数值大小反映了回归贡献的相对程度,即在因变量Y的总变异中回归关系所能解释的百分比。 R2是最常用于评价回归模型优劣程度的指标,R2越大(接近于1),所拟合的回归方程越优。
假设一数据集包括y1,...,yn共n个观察值,相对应的模型预测值分别为f1,...,fn。定义残差ei = yi − fi,平均观察值为
虽然R2可以用来评价回归方程的优劣,但随着自变量个数的增加,R2将不断增大(因为自变量个数的增加,意味着模型的复杂度升高,对样本数据的拟合程度会提高)。
若对两个具有不同个数自变量的回归方程进行比较时,不能简单地用R2作为评价回归方程的标准,还必须考虑方程所包含的自变量个数的影响,此时可用校正的决定系数(R2-adjusted)

其中n是样本数量,p是模型中变量的个数,当变量个数为0时,修正和原始的R方是一样的
就是相当于给变量的个数加惩罚项。换句话说,如果两个模型,样本数一样,R2一样,那么从修正R2的角度看,使用变量个数少的那个模型更优。
至于R2大于多少才有意义呢?这时我们可以看另外一个指标:复相关系数(Multiple correlation coefficient)R,R是决定系数R2的平方根,可用来度量因变量Y与多个自变量间的线性相关程度,即观察值Y与估计值之间的相关程度。
相关系数要在0.7~0.5才有意义,因此,R2应大于0.5*0.5=0.25,所以有种观点认为,在直线回归中应R2大于0.3才有意义。
还是来看下一个简单的例子,看下简单的平滑预测的R平方有多少

import numpy as np def r_square(y,f): y,f = np.array(y),np.array(f) y_mean = y.mean() SStot = sum(np.power((y-y_mean),2)) SSres = sum(np.power(y-f,2)) return 1.0 - 1.0*SSres/SStot def smooth_(squences,period=5): res = [] gap = period/2 right = len(squences) for i in range(right): res.append(np.mean(squences[i-gap if i-gap > 0 else 0:i+gap if i+gap < right else right])) return res httpspeedavg = np.array([1821000, 2264000, 2209000, 2203000, 2306000, 2005000, 2428000, 2246000, 1642000, 721000, 1125000, 1335000, 1367000, 1760000, 1807000, 1761000, 1767000, 1723000, 1883000, 1645000, 1548000, 1608000, 1372000, 1532000, 1485000, 1527000, 1618000, 1640000, 1199000, 1627000, 1620000, 1770000, 1741000, 1744000, 1986000, 1931000, 2410000, 2293000, 2199000, 1982000, 2036000, 2462000, 2246000, 2071000, 2220000, 2062000, 1741000, 1624000, 1872000, 1621000, 1426000, 1723000, 1735000, 1443000, 1735000, 2053000, 1811000, 1958000, 1828000, 1763000, 2185000, 2267000, 2134000, 2253000, 1719000, 1669000, 1973000, 1615000, 1839000, 1957000, 1809000, 1799000, 1706000, 1549000, 1546000, 1692000, 2335000, 2611000, 1855000, 2092000, 2029000, 1695000, 1379000, 2400000, 2522000, 2140000, 2614000, 2399000, 2376000]) httpavg = np.round((1.0*httpspeedavg/1024/1024).tolist(),2) smooth = np.round(smooth_((1.0*httpspeedavg/1024/1024).tolist(),5),2) print r_square(httpavg,smooth) # 0.711750424322
也就是71%的网络变化情况可以用平滑预测来解释