题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入输出格式
输入格式:第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式:一行,包含一个正整数,即为该网络的最大流。
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
样例说明:
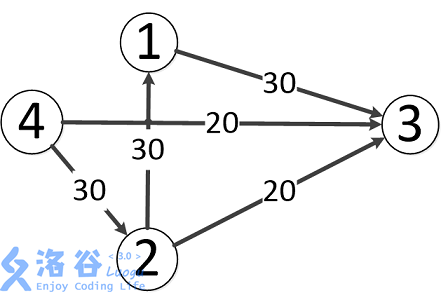
题目中存在3条路径:
4-->2-->3,该路线可通过20的流量
4-->3,可通过20的流量
4-->2-->1-->3,可通过10的流量(边4-->2之前已经耗费了20的流量)
故流量总计20+20+10=50。输出50。
题解
就是个模板题啊!QAQ
//其实就是挂个板子2333
1 /* 2 qwerta 3 P3376 【模板】网络最大流 4 Accepted 5 100 6 代码 C++,1.68KB 7 提交时间 2018-07-12 17:31:29 8 耗时/内存 9 140ms, 4847KB 10 */ 11 #include<cmath> 12 #include<queue> 13 #include<cstdio> 14 #include<cstring> 15 #include<iostream> 16 using namespace std; 17 struct emm{ 18 int e,f,v; 19 }a[200007];//邻接链表存边 20 int h[10007],cur[10007];//cur:当前弧优化(没什么用 21 int n,m,s,t; 22 int tot=1; 23 inline int read()//快读 24 { 25 char ch=getchar(); 26 int s=1,x=0; 27 while(ch<'0'||ch>'9'){if(ch=='-')s=-1;ch=getchar();} 28 while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 29 return s*x; 30 } 31 inline void con(int l,int r,int w)//加边 32 { 33 a[++tot].f=h[l]; 34 h[l]=tot; 35 //cur[l]=h[l]; 36 a[tot].e=r; 37 a[tot].v=w; 38 return; 39 } 40 inline void scan()//读入,建图 41 { 42 n=read(),m=read(),s=read(),t=read(); 43 for(int i=1;i<=m;++i) 44 { 45 int z=read(),y=read(),l=read(); 46 con(z,y,l); 47 con(y,z,0); 48 } 49 return; 50 } 51 //Dinic 52 queue<int>q;//bfs的queue 53 int d[100007];//分层图的深度 54 inline bool bfs() 55 { 56 memset(d,0,sizeof(d));//初始化 57 d[s]=1;//标记源点深度 58 q.push(s); 59 for(int i=1;i<=n;++i)cur[i]=h[i];//恢复cur数组 60 while(!q.empty()) 61 { 62 int now=q.front(); 63 q.pop(); 64 //扩张 65 for(int i=h[now];i;i=a[i].f) 66 if(!d[a[i].e]&&a[i].v)//若未被标记过并且该边在残量网络中 67 { 68 d[a[i].e]=d[now]+1; 69 q.push(a[i].e); 70 } 71 } 72 return d[t];//返回s,t是否联通 73 } 74 int dfs(int x,int al) 75 { 76 if(x==t||!al)return al; 77 int tot=0; 78 for(int i=cur[x];i;i=a[i].f) 79 { 80 cur[x]=i;//当前弧优化 81 if(d[a[i].e]==d[x]+1&&a[i].v) 82 { 83 int f=dfs(a[i].e,min(al,a[i].v));//往下找 84 if(f)//若非0 85 { 86 a[i].v-=f; 87 a[i^1].v+=f; 88 tot+=f; 89 al-=f; 90 if(!al)break; 91 } 92 } 93 } 94 if(!tot)d[x]=-1;//最有用的优化!(敲黑板 95 return tot;//返回流量值 96 } 97 inline void run()//运行 98 { 99 long long ans=0; 100 while(bfs())ans+=dfs(s,2147483647); 101 cout<<ans; 102 return; 103 } 104 int main()//超短主函数(当年码风真奇怪orz 105 { 106 scan(); 107 run(); 108 return 0; 109 }