二分图?
- 不存在奇环(长度为奇数的环)的图
- 节点能黑白染色,使得不存在同色图相连的图
这两个定义是等价哒。
直观而言,就是这样的图:
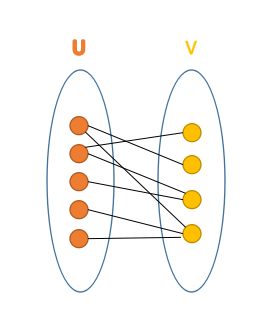
二分图有一些神奇的性质,让一些在一般图上复杂度飞天的问题可以在正常时间得到解。(这就是我们研究它的原因鸭!)
然后是一些可能会用到的定义(确实用到了 还搞得人一头懵逼QAQ
- 匹配:图中边的一个子集,使这些边没有公共顶点。
当边数最大化的时候,称这个边集为一组最大匹配。
- 独立集:图中点的一个子集,使点的导出子图中不存在边。
人话:选一些点,使得中间任意两个点之间没有边
- 覆盖:点的集合,使每条边至少跟子集中一个点关联。
人话:让图中的每条边至少有一个顶点在集合里。
- 支配集:一个神奇的点集,使每个点要么处于集合之中,要么和集合中至少一点关联
(被支配的恐惧
才讲完预备知识!惊不惊喜?!意不意外?!
求匹配的算法:
- 匈牙利算法
时间复杂度$O(NM)$,空间用邻接矩阵是$O(N^2)$,可以用邻接表优化。
- Dinic
时间复杂度$O(msqrt{n})$。
比匈牙利难码难理解,但是应用范围广多了(最大流算法
(会了这个还学什么匈牙利
———————————————————————————
—这里有一大段不知所云感觉没什么luan用的Hall定理—
———————————————————————————
König 定理
这个名字上风骚的两点让人忍不住觉得naïve。
这个定理就是讲了二分图的最大匹配,最大独立集,最小覆盖之间的关系。
首先设图的点数为N,最大匹配的大小为C
那么有最小覆盖=C,最大独立集=N-C
证明:
首先我们知道最小覆盖和最大独立集是对偶问题。
(把最小覆盖的点删掉,剩下来的就是最大独立集啦
然后就只要证明最小覆盖=最大匹配了
不证了,当结论记叭。(懒
其实是不会证。
EG1
有一个$n*m$的棋盘,其中有一些格子里有怪。
每次操作,可以选择一行或一列攻击,消灭这一行/列的所有怪。
求最少需要几次打掉所有怪。(1e5)
首先建一个二分图,左边$n$个点,代表行;右边$m$个点,代表列。
设这个怪所在的坐标为$(i,j)$,则把左边第$i$个点和右边第$j$个点连起来。
然后求一个最小覆盖就行啦。
EG2
有一个$n*m$的棋盘,其中有些格子放了马。
你要去掉一些马,使它们不能相互攻击。
求留下的马的最大值。(1e5)
因为马走日,所以如果两个格子能够相互攻击,也就意味着这两个格子不同色。
所以冲突必然在黑白两色之间。(阴阳之战,一触即发!
建二分图,一边黑,一边白,如果冲突就连边。
最后求最大独立集就行了。
小总结
- 以上是一些非常“简单直观”的套路。(???气哭
- 二分图是一个很强的性质,在做题的时候如果发现这是个二分图,就可以试着利用这个性质搞事情儿。
————————————
最小链覆盖
定义:在一个DAG中,选择尽可能少的链覆盖整个DAG,使每个点被覆盖至少一次。
求法:
首先给图求一个传递闭包,之后假定我们选的链两两不相交。
(传递闭包:若$i$能到$j$,且$j$能到$k$,则在$i$和$k$中间连条线。这样搞出来的图叫做原图的传递闭包。)
然后建个二分图:
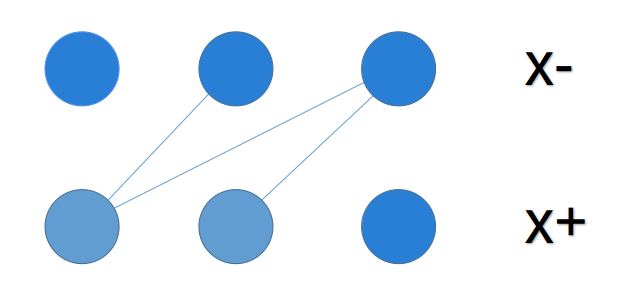
把每个点$x$拆成$x^{+},x^{-}$,如果原图存在有向边$x->y$,则连边$x^{+}->y^{-}$。
eg:如果有一张$1->2->3$的图,那么它建起来的二分图↓
然后无脑求个最大匹配,设结果为$C$。
那么这张二分图的最大独立集$=$点数$-C=2N-C$//图中亮色点
结合图像想想可知,每一个点$x$拆成$x^{+},x^{-}$后,$x^{-}$是肯定会亮的。
所以原图中的的链数应该要在二分图独立集基础上$-N$,即$2N-C-N=N-C$。
结论:最小链覆盖$=$点数$-$最大匹配
怎么说呢,这个结论总感觉看着这张图就有通了六脉的觉悟,又说不出来qwq
最长反链
定义:在一个DAG中,选出一些点构成集合$S$,若对任意$x_1,x_2 in S$,都有$x_1$走不到$x_2$,且$x_2$走不到$x_1$,那么我们说S是一个反链。
有Dilworth定理说,DAG上 最长反链的大小 等于 最小链覆盖的大小
也要用上面这张图通六脉。(还是不会证
————————————————————————
——然后就到欢欣鼓舞的网络流啦!(超开心——
————————————————————————
让我们在进入极乐净土之前回顾一下之前听到昏昏欲睡的知识:
- 二分图是一种超棒的图,有很多超棒的特性
- 我们可以用匈牙利算法或者Dinic求最大匹配
-
König 定理:最大匹配$=$最小覆盖$=$点数$-$最大独立集
- 最小链覆盖:先求个传递闭包,然后建二分图跑最大匹配。最小链覆盖$=$点数$-$最大匹配。
- 最长反链:任意两点都走不了的DAG,最长反链$=$最小链覆盖
都什么狗屁东西(摔
网络流
- 定义:有一个有向图,有源点S和汇点T,每条边有流量限制c。
- 最大流:一种流水的方法,使流入T的流量最大化。
- 注意在流水的过程中,除源点/汇点以外的点都是不积水的,也就是源点流出流量=汇点流入流量。
- 反向边:用来后悔的。与原边相反,初始流量为0。
- 残量网络:把图中所有流量为零的边(包括反向边)删掉,剩下来的图称为残量网络。
- 显然,只要残量网络中存在S到T的通路,那么就一定可以通过这条路使流入T的流量更大。
- 增广:我们把这样增流的操作称为增广,这条路径叫做增广路。
- 从而,一个流是最大流等价于不存在增广路,也即残量网络中S,T不连通。(Dinic中用bfs()判断能否增广的原理)
- 最小割:在初始图中割掉流量之和最小的一些边,使S,T不连通。
- 最大流最小割定理:最大流=最小割
- 证明略。(这次我是真的因为懒QAQ
算法
- EK
- 据说很好懂?入门级算法叭
- 理论复杂度$O(NM^{2})$,超慢。
- 反正我不会。
- Dinic
- 最常见的叭。
- 理论复杂度$O(MN^{2})$,但是通常(绝绝绝大多数时候)跑不到。
- 不像SPFA总是被卡,通常没人卡Dinic。$n<=1e5$的数据都随便跑。
- 反正我就会这个,这里是我的板子。
- ISAP
- 不像Dinic要跑多次bfs,ISAP只需要跑一次。
- 所以比Dinic快,但是应该(应该?)快不了多少叭。
- 反正我不会。(省选再说吧QAQ)
——————
好累啊,去做点题休息休息?QAQ
接下来就是一些题了(估计要集训完才有时间再整理了叭
我真棒。
——————
10.13UPD:自从学了这些鬼东西之后,连dp都变成网络流水题了。
这些结论是真的好用!无脑的感觉真棒qaq