题目描述
给定一个n × m的矩形地图,每个各自上可能为空,可能有牌,牌上有一个数字。
对于两张同样数字的牌,如果我们可以在地图上用不超过三根水平或竖直,在地图界内,且不经过其他牌的线段将两张牌连起来,那么我们这一对牌是可以被消去的。
比如下图中,两张1可以被消去,但是2和3都不能被消去。 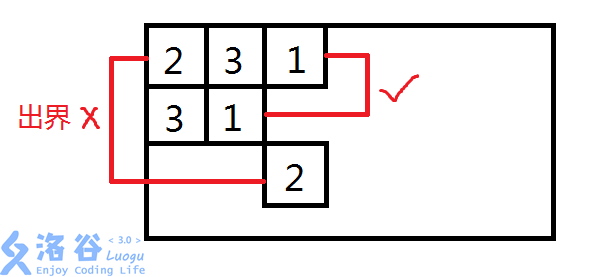
现在给出一个n × m的连连看地图,其中有2k张牌,保证每张牌上的数字都在[1, k]范围内,且每个数字都只会出现两次,问目前有多少对牌是可以消去的。
输入输出格式
输入格式:
输入第一行三个正整数n, m, k,分别代表地图的长,宽以及牌的对数。
接下来k行每行四个正整数x1 , y1 , x2 , y2,表示数字为k的两张牌的位置。
输出格式:
输出仅一行一个整数,表示当前可以消去的牌的对数
输入输出样例
说明
30%的数据 n, m≤ 20,k<=min(3, ⌊ n*m/2 ⌋)
接下来30%的数据 n, m≤ 100,k<=min(100, ⌊ n*m/2 ⌋)
接下来30%的数据 n, m≤ 1000,k<=min(5000, ⌊ n*m/2 ⌋)
题解
考虑数据范围很小,我们可以做各种n方操作。
读入的同时把相应坐标标记
flag[ i ] [ j ]=1;套两个for循环,分别求横排上的前缀和 及竖排上的前缀和
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
ss[i][j]=ss[i-1][j]+tu[i][j],
hs[i][j]=hs[i][j-1]+tu[i][j];对于每组牌:
我们把一张牌分别向上下左右暴力走,走到边界或障碍就停,经过的点就标记。(画十字)
|____________|
| O |
| | O |
| | |
| O——O————O|
| | |
| | |
| O | |
|______|_____|然后把第二张牌也上下左右暴力走,同样经过则标记。如果有到被标记过的点,说明路线相交了,这对牌可消,flag=1
若未相交:
从1~n枚举横坐标j,如果这一段(< x1 , j >点到 < x2 , j >点)上的区间和为0
且< x1 , j >点和< x2 , j >点被标记过(画十字的时候经历过)的话(用前缀和O(1)查询)
则这一段没有障碍,可以连线,flag=1
从1~n枚举纵坐标i,如果< i , y1 >点到< i , y2 >上的区间和为0,则可连,flag=1
最后如果flag为1,则ans++
代码://考场代码
1 #include<algorithm> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 using namespace std; 7 inline int read()//快读 8 { 9 char ch=getchar(); 10 int x=0;bool s=1; 11 while(ch<'0'||ch>'9'){if(ch=='-')s=0;ch=getchar();} 12 while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 13 return s?x:-x; 14 } 15 int lx[5007],ly[5007],rx[5007],ry[5007]; 16 int ss[1007][1007]; 17 int hs[1007][1007]; 18 bool tu[1007][1007]; 19 bool sf[1007][1007]; 20 int main() 21 { 22 int n=read(),m=read(),k=read(); 23 for(int i=1;i<=k;++i) 24 { 25 lx[i]=read(), 26 ly[i]=read(), 27 rx[i]=read(), 28 ry[i]=read(); 29 tu[lx[i]][ly[i]]=1; 30 tu[rx[i]][ry[i]]=1;//标记 31 } 32 for(int i=0;i<=n+1;++i) 33 tu[i][0]=tu[i][m+1]=1; 34 for(int i=0;i<=m+1;++i) 35 tu[0][i]=tu[n+1][i]=1; 36 for(int i=1;i<=n;++i) 37 for(int j=1;j<=m;++j) 38 ss[i][j]=ss[i-1][j]+tu[i][j], 39 hs[i][j]=hs[i][j-1]+tu[i][j];//前缀和 40 int ans=0; 41 for(int c=1;c<=k;++c) 42 { 43 int flag=0; 44 memset(sf,0,sizeof(sf)); 45 //以下一大堆为画十字 46 tu[lx[c]][ly[c]]=0; 47 tu[rx[c]][ry[c]]=0;//便于之后操作 48 int x=lx[c],y=ly[c]; 49 int l,r,u,d; 50 while(!tu[x][y]){sf[x--][y]=1;} 51 u=x+1; 52 x=lx[c]+1,y=ly[c]; 53 while(!tu[x][y]){sf[x++][y]=1;} 54 d=x-1; 55 x=lx[c],y=ly[c]-1; 56 while(!tu[x][y]){sf[x][y--]=1;} 57 l=y+1; 58 x=lx[c],y=ly[c]+1; 59 while(!tu[x][y]){sf[x][y++]=1;} 60 r=y-1; 61 x=rx[c],y=ry[c]; 62 while(!tu[x][y]){if(sf[x][y])flag++;sf[x--][y]=1;} 63 u=max(u,x+1); 64 x=rx[c]+1,y=ry[c]; 65 while(!tu[x][y]){if(sf[x][y])flag++;sf[x++][y]=1;} 66 d=min(d,x-1); 67 x=rx[c],y=ry[c]-1; 68 while(!tu[x][y]){if(sf[x][y])flag++;sf[x][y--]=1;} 69 l=max(l,y+1); 70 x=rx[c],y=ry[c]+1; 71 while(!tu[x][y]){if(sf[x][y])flag++;sf[x][y++]=1;} 72 r=min(r,y-1); 73 //画十字结束 74 if(!flag) 75 { 76 int zx=lx[c],zy=ly[c],yx=rx[c],yy=ry[c]; 77 if(zx>yx)swap(zx,yx); 78 if(zy>yy)swap(zy,yy); 79 for(int i=u;i<=d;++i)//枚举横坐标 80 if(hs[i][yy]-hs[i][zy-1]==0)flag++; 81 for(int j=l;j<=r;++j)//枚举纵坐标 82 if(ss[yx][j]-ss[zx-1][j]==0)flag++; 83 } 84 if(flag)ans++; 85 tu[lx[c]][ly[c]]=1; 86 tu[rx[c]][ry[c]]=1;//复原 87 //cout<<flag<<endl; 88 } 89 cout<<ans;//强大怪!!! 90 return 0; 91 }
//强大怪!!!(滑稽