在之前的博文基于theano的深度卷积神经网络中使用了theano.tensor.nnet.conv.conv2d函数来计算神经网络的卷积。
计算过程如下图所示。

尽管下面的代码也能实现相应的功能,但是速度慢了很多。
def conv(self,a, v, full=0): # valid:0 full:1 ah, aw = np.shape(a) vh, vw = np.shape(v) if full: temp = np.zeros((ah + 2 * vh - 2, aw + 2 * vw - 2)) temp[vh - 1:vh - 1 + ah, vw - 1:vw - 1 + aw] = a a = temp ah, aw = np.shape(a) k = [[np.sum(np.multiply(a[i:i+vh,j:j+vw],v)) for j in range(aw - vw + 1)] for i in range(ah - vh + 1)] return k
下面简单使用一下theano.tensor.nnet.conv.conv2d。
输入层为2*1*4*4,卷积核为2*1*2*2,得到的结果是2*2*3*3。每个4*4的输入各与两个卷积核运算,每次输入1个,得到2*2*3*3的输出。
filter_shape=(2,1,2,2),image_shape=(2,1,4,4)为可选参数,此处使用结果也一样。
当输入层第二个参数n不为1时,卷积核第二个参数需要等于n,每次输入n个,结果为分别卷积之和。
在进行上图所示卷积运算之前,卷积核先要旋转180度。
比如,对于结果第一行的 [ 0. 0.1 0.3 ] 计算方式是:
用[[ 0.3 , 0.2 ] 分别点乘 [[ 0 , 0 ] 、 [[ 0 , 0 ] 和 [[ 0 , 0 ] 。
[ 0.1 , 0 ]] [ 0 , 0.1]] [ 0.1, 0.3 ]] [ 0.3 , 0 ]]
import numpy as np import theano from theano.tensor.nnet import conv import theano.tensor as T inputs = T.tensor4(name='input', dtype='float64') a=np.array(range(8)) a=a*0.1 a=np.reshape(a,(2,1,2,2)) W = theano.shared( np.asarray( a, dtype=inputs.dtype), name='W') conv_out = conv.conv2d(inputs, W,filter_shape=(2,1,2,2),image_shape=(2,1,4,4)) f = theano.function([inputs], conv_out) x = np.asarray([ [[[0, 0, 0, 0], [0, 1, 3, 0], [0, 2, 2, 0], [0, 0, 0, 0]]], [[[0, 0, 0, 0], [0, 2, 1, 0], [0, 1, 1, 0], [0, 0, 0, 0]]] ], dtype='float64') y= f(x) print(y) # 2,2,3,3 """ [[[[ 0. 0.1 0.3] [ 0.2 1.1 1.1] [ 0.4 1. 0.6]] [[ 0.4 1.7 1.5] [ 1.4 4.3 3.1] [ 1.2 2.6 1.4]]] [[[ 0. 0.2 0.1] [ 0.4 0.9 0.4] [ 0.2 0.5 0.3]] [[ 0.8 1.4 0.5] [ 1.6 2.9 1.2] [ 0.6 1.3 0.7]]]] """
在源码中调用了scipy.signal.sigtool._concolve2d。

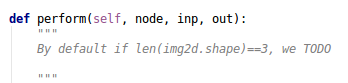
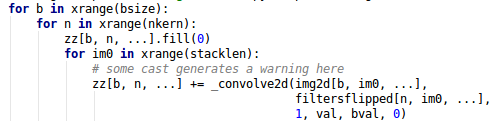
scipy.signal.sigtool.concolve2d与numpy.convolve都能实现,下面是简单的示例。
concolve2d对单个输入与卷积核的运算,在valid模式下得到的结果和theano中一样。
convolve将除了首尾两行外的其余列两两相加得到的结果与convolve2d一样。
convolve计算比较简单, 如 np.convolve([1 , 2 , 3 ], [ 2 ,3 ,4 ])得到[ 2 7 16 17 12],等于[2,3,4]分别乘[1,2,3]并错位相加的结果。
import scipy.signal.signaltools as sg import numpy as np a = [[0, 0, 0, 0], [0, 1, 3, 0], [0, 2, 2, 0], [0, 0, 0, 0]] b = [[0, 0.1], [0.2, 0.3]] e = sg.convolve2d(a, b) print e """ [[ 0. 0. 0. 0. 0. ] [ 0. 0. 0.1 0.3 0. ] [ 0. 0.2 1.1 1.1 0. ] [ 0. 0.4 1. 0.6 0. ] [ 0. 0. 0. 0. 0. ]] """ ne=[np.convolve(ai,bi) for ai in a for bi in b] for ni in ne: print ni """ [ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.] [ 0. 0. 0.1 0.3 0. ] [ 0. 0.2 0.9 0.9 0. ] [ 0. 0. 0.2 0.2 0. ] [ 0. 0.4 1. 0.6 0. ] [ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.] """ print sg.convolve2d(a, b, 'valid') """ [[ 0. 0.1 0.3] [ 0.2 1.1 1.1] [ 0.4 1. 0.6]] """
自己写一个简单的,速度差别很大。
import scipy.signal.signaltools as sg import numpy as np import timeit a = [[1,2,3,4,1,2,3,4,1,2,3,4,1,2,3,4]] b = [[1,2,3,4,1,2,3,4,1,2,3,4,1,2,3,4]] def conv1d(a,b): m=len(a) n=len(b) t = m + n - 1 r = [0] * t for i in range(t): for j in range(min(m,i+1)): if (i - j < n): r[i] += a[j] * b[i-j] return r def npconv(): np.convolve(a[0],b[0]) def sgconv(): sg.convolve2d(a, b) def newconv(): conv1d(a[0], b[0]) if __name__=='__main__': print sg.convolve2d(a, b) print np.convolve(a[0], b[0]) print conv1d(a[0], b[0]) print timeit.timeit('sgconv()',setup='from __main__ import sgconv',number=10000) print timeit.timeit('npconv()',setup='from __main__ import npconv',number=10000) print timeit.timeit('newconv()',setup='from __main__ import newconv',number=10000) """ [[ 1 4 10 20 27 32 36 40 53 60 62 60 79 88 88 80 103 108 60 77 80 68 40 51 52 42 20 25 24 16]] [ 1 4 10 20 27 32 36 40 53 60 62 60 79 88 88 80 103 108 60 77 80 68 40 51 52 42 20 25 24 16] [1, 4, 10, 20, 27, 32, 36, 40, 53, 60, 62, 60, 79, 88, 88, 80, 103, 108, 94, 60, 77, 80, 68, 40, 51, 52, 42, 20, 25, 24, 16] 0.163667983502 0.0639453593833 0.62897722497 """
附scipy.signal.signaltools.convolve2d源码。
def convolve2d(in1, in2, mode='full', boundary='fill', fillvalue=0): ...... out = sigtools._convolve2d(in1, in2, 1, val, bval, fillvalue) ...... return out
static PyObject *sigtools_convolve2d(PyObject *NPY_UNUSED(dummy), PyObject *args) { ...... ret = pylab_convolve_2d (PyArray_DATA(ain1), /* Input data Ns[0] x Ns[1] */ PyArray_STRIDES(ain1), /* Input strides */ PyArray_DATA(aout), /* Output data */ PyArray_STRIDES(aout), /* Ouput strides */ PyArray_DATA(ain2), /* coefficients in filter */ PyArray_STRIDES(ain2), /* coefficients strides */ PyArray_DIMS(ain2), /* Size of kernel Nwin[2] */ PyArray_DIMS(ain1), /* Size of image Ns[0] x Ns[1] */ flag, /* convolution parameters */ PyArray_DATA(newfill)); /* fill value */ ...... }
int pylab_convolve_2d (char *in, /* Input data Ns[0] x Ns[1] */ intp *instr, /* Input strides */ char *out, /* Output data */ intp *outstr, /* Ouput strides */ char *hvals, /* coefficients in filter */ intp *hstr, /* coefficients strides */ intp *Nwin, /* Size of kernel Nwin[0] x Nwin[1] */ intp *Ns, /* Size of image Ns[0] x Ns[1] */ int flag, /* convolution parameters */ char *fillvalue) /* fill value */ { int bounds_pad_flag = 0; int m, n, j, ind0, ind1; int Os[2]; int new_m, new_n, ind0_memory=0; int boundary, outsize, convolve, type_num, type_size; char ** indices; OneMultAddFunction *mult_and_add; boundary = flag & BOUNDARY_MASK; /* flag can be fill, reflecting, circular */ outsize = flag & OUTSIZE_MASK; convolve = flag & FLIP_MASK; type_num = (flag & TYPE_MASK) >> TYPE_SHIFT; /*type_size*/ mult_and_add = OneMultAdd[type_num]; if (mult_and_add == NULL) return -5; /* Not available for this type */ if (type_num < 0 || type_num > MAXTYPES) return -4; /* Invalid type */ type_size = elsizes[type_num]; if (outsize == FULL) {Os[0] = Ns[0]+Nwin[0]-1; Os[1] = Ns[1]+Nwin[1]-1;} else if (outsize == SAME) {Os[0] = Ns[0]; Os[1] = Ns[1];} else if (outsize == VALID) {Os[0] = Ns[0]-Nwin[0]+1; Os[1] = Ns[1]-Nwin[1]+1;} else return -1; /* Invalid output flag */ if ((boundary != PAD) && (boundary != REFLECT) && (boundary != CIRCULAR)) return -2; /* Invalid boundary flag */ indices = malloc(Nwin[1] * sizeof(indices[0])); if (indices == NULL) return -3; /* No memory */ /* Speed this up by not doing any if statements in the for loop. Need 3*3*2=18 different loops executed for different conditions */ for (m=0; m < Os[0]; m++) { /* Reposition index into input image based on requested output size */ if (outsize == FULL) new_m = convolve ? m : (m-Nwin[0]+1); else if (outsize == SAME) new_m = convolve ? (m+((Nwin[0]-1)>>1)) : (m-((Nwin[0]-1) >> 1)); else new_m = convolve ? (m+Nwin[0]-1) : m; /* VALID */ for (n=0; n < Os[1]; n++) { /* loop over columns */ char * sum = out+m*outstr[0]+n*outstr[1]; memset(sum, 0, type_size); /* sum = 0.0; */ if (outsize == FULL) new_n = convolve ? n : (n-Nwin[1]+1); else if (outsize == SAME) new_n = convolve ? (n+((Nwin[1]-1)>>1)) : (n-((Nwin[1]-1) >> 1)); else new_n = convolve ? (n+Nwin[1]-1) : n; /* Sum over kernel, if index into image is out of bounds handle it according to boundary flag */ for (j=0; j < Nwin[0]; j++) { ind0 = convolve ? (new_m-j): (new_m+j); bounds_pad_flag = 0; if (ind0 < 0) { if (boundary == REFLECT) ind0 = -1-ind0; else if (boundary == CIRCULAR) ind0 = Ns[0] + ind0; else bounds_pad_flag = 1; } else if (ind0 >= Ns[0]) { if (boundary == REFLECT) ind0 = Ns[0]+Ns[0]-1-ind0; else if (boundary == CIRCULAR) ind0 = ind0 - Ns[0]; else bounds_pad_flag = 1; } if (!bounds_pad_flag) ind0_memory = ind0*instr[0]; if (bounds_pad_flag) { intp k; for (k=0; k < Nwin[1]; k++) { indices[k] = fillvalue; } } else { intp k; for (k=0; k < Nwin[1]; k++) { ind1 = convolve ? (new_n-k) : (new_n+k); if (ind1 < 0) { if (boundary == REFLECT) ind1 = -1-ind1; else if (boundary == CIRCULAR) ind1 = Ns[1] + ind1; else bounds_pad_flag = 1; } else if (ind1 >= Ns[1]) { if (boundary == REFLECT) ind1 = Ns[1]+Ns[1]-1-ind1; else if (boundary == CIRCULAR) ind1 = ind1 - Ns[1]; else bounds_pad_flag = 1; } if (bounds_pad_flag) { indices[k] = fillvalue; } else { indices[k] = in+ind0_memory+ind1*instr[1]; } bounds_pad_flag = 0; } } mult_and_add(sum, hvals+j*hstr[0], hstr[1], indices, Nwin[1]); } } } free(indices); return 0; }