介绍摘自李航《统计学习方法》
EM算法
EM算法是一种迭代算法,1977年由Dempster等人总结提出,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计。EM算法的每次迭代由两步组成:E步,求期望(expectation);M步,求极大(maximization)。所以这一算法称为期望极大算法(expectation maximization algorithm),简称EM算法。本章首先叙述EM算法,然后讨论EM算法的收敛性;作为EM算法的应用,介绍高斯混合模型的学习;最后叙述EM算法的推广——GEM算法。
将观测数据表示为Y=(Y1,Y2,…,Yn)T,未观测数据表示为Z=(Z1,Z2,…,Zn)T,则观测数据的似然函数为

即
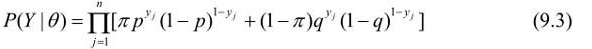
考虑求模型参数=(
Π,p,q)的极大似然估计,即

这个问题没有解析解,只有通过迭代的方法求解。EM算法就是可以用于求解这个问题的一种迭代算法。下面给出针对以上问题的EM算法,其推导过程省略。
EM算法首先选取参数的初值,记作(0)=(
Π(0),p(0),q(0)),然后通过下面的步骤迭代计算参数的估计值,直至收敛为止。第i次迭代参数的估计值为
(i)=(
(i),p(i),q(i))。EM算法的第i+1次迭代如下。
E步:计算在模型参数Π(i),p(i),q(i)下观测数据yj来自掷硬币B的概率
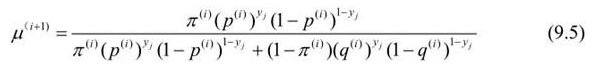
M步:计算模型参数的新估计值
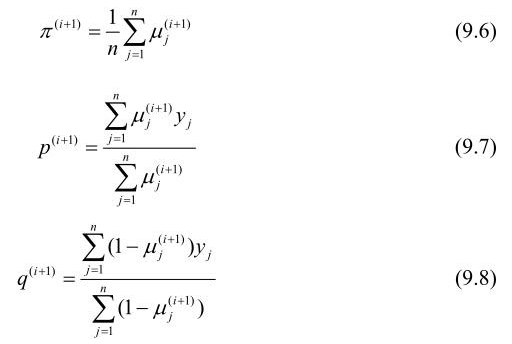
EM算法在高斯混合模型学习中的应用
EM算法的一个重要应用是高斯混合模型的参数估计。高斯混合模型应用广泛,在许多情况下,EM算法是学习高斯混合模型(Gaussian misture model)的有效方法。
定义9.2(高斯混合模型) 高斯混合模型是指具有如下形式的概率分布模型:

高斯混合模型参数估计的EM算法

1.明确隐变量,写出完全数据的对数似然函数
可以设想观测数据yj,j=1,2,…,N,是这样产生的:首先依概率ak选择第k个高斯分布分模型Ø(y|θk);然后依第k个分模型的概率分布Ø(y|
θk)生成观测数据yj。这时观测数据yj,j=1,2,…,N,是已知的;反映观测数据yj来自第k个分模型的数据是未知的,k=1,2,…,K,以隐变量
γjk表示,其定义如下:

有了观测数据yj及未观测数据γjk,那么完全数据是
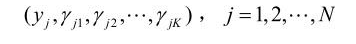
于是,可以写出完全数据的似然函数:

2.EM算法的E步:确定Q函数
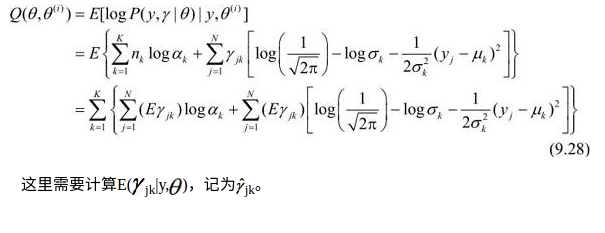

3.确定EM算法的M步
迭代的M步是求函数Q(θ,θ
(i))对
的极大值,即求新一轮迭代的模型参数:
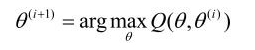


重复以上计算,直到对数似然函数值不再有明显的变化为止。
1 # coding:utf-8 2 import numpy as np 3 4 def qq(y,alpha,mu,sigma,K,gama):#计算Q函数 5 gsum=[] 6 n=len(y) 7 for k in range(K): 8 gsum.append(np.sum([gama[j,k] for j in range(n)])) 9 return np.sum([g*np.log(ak) for g,ak in zip(gsum,alpha)])+ 10 np.sum([[np.sum(gama[j,k]*(np.log(1/np.sqrt(2*np.pi))-np.log(np.sqrt(sigma[k]))-1/2/sigma[k]*(y[j]-mu[k])**2)) 11 for j in range(n)] for k in range(K)]) #《统计学习方法》中公式9.29有误 12 13 def phi(mu,sigma,y): #计算phi 14 return 1/(np.sqrt(2*np.pi*sigma)*np.exp(-(y-mu)**2/2/sigma)) 15 16 def gama(alpha,mu,sigma,i,k): #计算gama 17 sumak=np.sum([[a*phi(m,s,i)] for a,m,s in zip(alpha,mu,sigma)]) 18 return alpha[k]*phi(mu[k],sigma[k],i)/sumak 19 20 def dataN(length,k):#生成数据 21 y=[np.random.normal(5*j,j+5,length/k) for j in range(k)] 22 return y 23 24 def EM(y,K,iter=1000): #EM算法 25 n = len(y) 26 sigma=[10]*K 27 mu=range(K) 28 alpha=np.ones(K) 29 qqold,qqnew=0,0 30 for it in range(iter): 31 gama2=np.ones((n,K)) 32 for k in range(K): 33 for i in range(n): 34 gama2[i,k]=gama(alpha,mu,sigma,y[i],k) 35 for k in range(K): 36 sum_gama=np.sum([gama2[j,k] for j in range(n)]) 37 mu[k]=np.sum([gama2[j,k]*y[j] for j in range(n)])/sum_gama 38 sigma[k]=np.sum([gama2[j,k]*(y[j]-mu[k])**2 for j in range(n)])/sum_gama 39 alpha[k]=sum_gama/n 40 qqnew=qq(y,alpha,mu,sigma,K,gama2) 41 if abs(qqold-qqnew)<0.000001: 42 break 43 qqold=qqnew 44 return alpha,mu,sigma 45 46 N = 500 47 k=2 48 data=dataN(N,k) 49 y=np.reshape(data,(1,N)) 50 a,b,c = EM(y[0], k) 51 print a,b,c 52 # iter=180 53 #[ 0.57217609 0.42782391] [4.1472879054766887, 0.72534713118155769] [44.114682884921415, 24.676116557533351] 54 55 sigma = 6 #网上的数据 56 miu1 = 40 57 miu2 = 20 58 X = np.zeros((1, N)) 59 for i in xrange(N): 60 if np.random.random() > 0.5: 61 X[0, i] = np.random.randn() * sigma + miu1 62 else: 63 X[0, i] = np.random.randn() * sigma + miu2 64 a,b,c = EM(X[0], k) 65 print a,b,c 66 # iter=114 67 #[ 0.44935959 0.55064041] [40.561782615819361, 21.444533254494189] [33.374144230703514, 51.459622219329155]